Для построения доверительных интервалов для параметров генеральных совокупностей могут быть реализованы два подхода, основанных на знании точного (при данном объеме выборки п) или асимптотического (при п ->оо) распределения выборочных характеристик (или некоторых функций от них). Первый подход реализован далее при построении интервальных оценок параметров для малых выборок. В данном параграфе рассматривается второй подход, применимый для больших выборок (порядка сотен наблюдений).
Теорема. Вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число 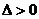 (по абсолютной величине), равна:
(по абсолютной величине), равна:
 , где
, где  (23)
(23)
 , где
, где 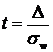 (24)
(24)
 - функция (интеграл вероятности) Лапласса
- функция (интеграл вероятности) Лапласса
Выше (§ 9.4) показано, что выборочная средняя  и выборочная доля
и выборочная доля  повторной выборки представляют сумму n независимых случайных величин
повторной выборки представляют сумму n независимых случайных величин  , где
, где 
имеет один и тот же закон распределения — соответственно (13) и (10) с конечными математическим ожиданием и дисперсией. Следовательно, на основании теоремы Ляпунова при  распределения
распределения  и
и  неограниченно приближаются к нормальным (практически при
неограниченно приближаются к нормальным (практически при  распределения
распределения  и
и  можно считать приближенно нормальными).
можно считать приближенно нормальными).
Для бесповторной выборки  и
и  представляют сумму зависимых случайных величин. Однако
представляют сумму зависимых случайных величин. Однако 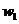 можно показать, что и в этом случае при
можно показать, что и в этом случае при  закон распределения
закон распределения  и
и  как угодно близко приближается к нормальному.
как угодно близко приближается к нормальному.
Формулы (23) и (24) следуют непосредственно из свойства 2 нормального закона формулы.
Формулы (23) и (24) получили название формул доверительной вероятности для средней и доли.
Определение. Среднее квадратическое отклонение выборочной средней 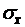 и выборочной доли
и выборочной доли  собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки.(Для бесповторной выборки обозначаем соответствено
собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки.(Для бесповторной выборки обозначаем соответствено 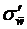 и
и  ).
).
Из рассмотренной теоремы вытекают следующие следствия.
Следствие 1. При заданной доверительной вероятности 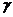 предельная ошибка выборки равна (-кратной величине средней квадра-тической ошибки, где
предельная ошибка выборки равна (-кратной величине средней квадра-тической ошибки, где 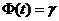 , т.е.
, т.е.
(25)
(26)
Следствие 2. Интервальные оценки {доверительные интервалы) для генеральной средней и генеральной доли могут быть найдены по формулам:
 (28), (27)
(28), (27)
Формулы средних квадратических ошибок выборки  ,
, 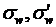 могут быть легко получены из формул (16), (17), (11), (12) соответствующих дисперсий
могут быть легко получены из формул (16), (17), (11), (12) соответствующих дисперсий  . Поместим их в таблицу:
. Поместим их в таблицу:
Таблица 2
| Оцениваемый
параметр
| Формулы средних квадратических ошибок выборки
|
| повторная выборка
| бесповторная выборка
|
| Средняя
| 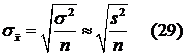
| 
|
| Доля
| 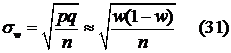
| 
|
Так как генеральные доля р и дисперсия  неизвестны, то в формулах табл. 2 заменяем их состоятельными оценками по выборке — соответственно
неизвестны, то в формулах табл. 2 заменяем их состоятельными оценками по выборке — соответственно  и
и  , ибо при достаточно большом объеме выборки п практически достоверно, что
, ибо при достаточно большом объеме выборки п практически достоверно, что  .
.
При определении средней квадратической ошибки выборки для доли, если даже  неизвестна, в качестве
неизвестна, в качестве  можно взять его максимально возможное значение
можно взять его максимально возможное значение 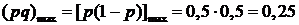 , (так как
, (так как  то рq максимально при р = 0,5).
то рq максимально при р = 0,5).
Объем выборки. Для проведения выборочного наблюдения весьма важно правильно установить объем выборки п, который в значительной степени определяет необходимые при этом временные, трудовые и стоимостные затраты. Для определения п необходимо задать надежность (доверительную вероятность) оценки  и точность (предельную ошибку выборки)
и точность (предельную ошибку выборки) 
Объем выборки находится из формулы, выражающей предельную ошибку выборки через дисперсию признака. Например, для повторной выборки при оценке генеральной средней с надежностью  с учетом (25) и (29) эта формула имеет вид:
с учетом (25) и (29) эта формула имеет вид:
 откуда
откуда  , где
, где  . Аналогично могут быть получены и другие формулы объема выборки, которые сведем в таблицу:
. Аналогично могут быть получены и другие формулы объема выборки, которые сведем в таблицу:
| Оцениваемый параметр
| Повторная выборка
| Бесповторная выборка
|
| Генеральная средняя
|  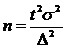
| 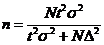
|
| Генеральная доля
| 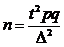
|
|
Если найден объем повторной выборки п, то объем соответствующей бесповторной выборки п' можно определить по формуле:
 , (37)
, (37)
Так как  , то при одних и тех же точности и надежности оценок объем бесповторной выборки n всегда меньше объема повторной выборки
, то при одних и тех же точности и надежности оценок объем бесповторной выборки n всегда меньше объема повторной выборки  . Этим и объясняется тот факт, что на практике в основном используется бесповторная выборка.
. Этим и объясняется тот факт, что на практике в основном используется бесповторная выборка.
Как видно из формул (33)—(36), для определения объема выборки необходимо знать характеристики генеральной совокупности 
 или р, которые неизвестны и для определения которых предполагается провести выборочное наблюдение. В качестве этих характеристик обычно используют выборочные данные
или р, которые неизвестны и для определения которых предполагается провести выборочное наблюдение. В качестве этих характеристик обычно используют выборочные данные  или
или  предшествующего исследования в аналогичных условиях, т.е. полагают
предшествующего исследования в аналогичных условиях, т.е. полагают  (или)
(или)  или
или  .
.
Если никаких сведений о значениях  или р нет, то организуют специальную пробную выборку небольшого объема, находят оценку
или р нет, то организуют специальную пробную выборку небольшого объема, находят оценку  (более точную, чем
(более точную, чем  для малой выборки) или
для малой выборки) или  и, полагая
и, полагая 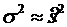 или
или  , находят объем «основной» выборки.
, находят объем «основной» выборки.
При оценке генеральной доли (если о ней ничего неизвестно) вместо проведения пробной выборки можно в формулах (35), (36) в качестве рq = р(1 - р) взять его максимально возможное значение, равное 0,25, но при этом надо учитывать, что найденное значение объема выборки будет больше (иногда существенно больше) минимально необходимого для заданных точности и надежности оценок.
Объем бесповторной выборки п' мог быть вычислен и по (37), так как уже известен объем повторной выборки п, т.е.

Как видим, при одной и той же точности  и надежности
и надежности  = 0,9973 оценки объем бесповторной выборки существенно меньше, чем повторной.
= 0,9973 оценки объем бесповторной выборки существенно меньше, чем повторной.
Замечание. Если генеральная совокупность бесконечна  , либо объем бесповторной выборки значительно меньше объема генеральной совокупности
, либо объем бесповторной выборки значительно меньше объема генеральной совокупности  , расчеты средних квадратических ошибок (для средней и доли) и необходимого объема бесповторной выборки следует проводить по соответствующим формулам для повторной выборки.
, расчеты средних квадратических ошибок (для средней и доли) и необходимого объема бесповторной выборки следует проводить по соответствующим формулам для повторной выборки.
Построение доверительного интервала для генеральной доли по умеренно большим выборкам. Объем выборки может быть не настолько велик (например, десятки наблюдений), чтобы использовать приближенную формулу (31)  Вместо точной
Вместо точной 
В то же время распределение выборочной доли  можно по-прежнему считать приближенно нормальным. В этом случае, учитывая (24), (26), доверительный интервал для генеральной доли рследует искать из условия
можно по-прежнему считать приближенно нормальным. В этом случае, учитывая (24), (26), доверительный интервал для генеральной доли рследует искать из условия
 . (38)
. (38)
Возводя обе части неравенства (9.38) в квадрат, преобразуем его к равносильному:
 , (39)
, (39)
Областью решения неравенства (39) является внутренняя часть эллипса, проходящего через точки (0;0) и (1;1) и имеющего в этих точках касательные, параллельные оси абсцисс.
Так как величина  заключена между 0 и 1, то область
заключена между 0 и 1, то область  нужно еще ограничить слева и справа прямыми
нужно еще ограничить слева и справа прямыми  (наличие «лишних» областей, выходящих за полосу
(наличие «лишних» областей, выходящих за полосу  , объясняется тем, что при значениях р, близких к 0 или 1. допущение о нормальном законе распределения
, объясняется тем, что при значениях р, близких к 0 или 1. допущение о нормальном законе распределения  становится неправомерным).
становится неправомерным).
По найденному по выборке значению  границы доверительного интервала
границы доверительного интервала  для р определяются как точки пересечения соответствующей вертикальной прямой с эллипсом (рис. 2). Чем больше объем выборки п, тем «доверительный эллипс» более вытянут, тем уже доверительный интервал.
для р определяются как точки пересечения соответствующей вертикальной прямой с эллипсом (рис. 2). Чем больше объем выборки п, тем «доверительный эллипс» более вытянут, тем уже доверительный интервал.

Рис. 2
Границы р1 и р2 доверительного интервала для р могут быть найдены из соотношения (39) по формуле:
 , (40)
, (40)
В случае больших выборок, при  , величинами
, величинами  (по сравнению с 1),
(по сравнению с 1),  (по сравнению с
(по сравнению с  ),
),  (по сравнению с
(по сравнению с  можно пренебречь, и получим:
можно пренебречь, и получим:

т.е. доказанные ранее формулы (28) и (26).
Корреляция и регрессия. Функциональная, статистическая и корреляционная зависимость между переменными. Линейная парная корреляционная связь. Коэффициент корреляции, его вычисления и сво-ва. Линейная парная регрессия. Метод наименьших квадратов для оценки параметров регрессии. Прогноз неизвестных экономических показателей по известным значениям других.
КОРРЕЛЯЦИЯ — (лат. correlatio — взаимосвязь) — в статистике: понятие, отражающее наличие связи между явлениями, процессами и характеризующими их величинами.
РЕГРЕССИЯ-зависимость между зависимой переменной Y и одной или несколькими независимыми переменными
Диалектический подход к изучению природы и общества требует рассмотрения явлений в их взаимосвязи и непрестанном изменении.
Понятия корреляции и регрессии появились в середине XIX в. благодаря работам английских статистиков Ф. Гальтона и К. Пирсона. Первый термин произошел от латинского «correlatio» — соотношение, взаимосвязь. Второй термин (от лат. «regressio» — движение назад) введен Ф. Гальтоном, который, изучая зависимость между ростом родителей и их детей, обнаружил явление «регрессии к среднему» — у детей, родившихся у очень высоких родителей, рост имел тенденцию быть ближе к средней величине.
В естественных науках часто речь идет о функциональной зависимости (связи), когда каждому значению одной переменной соответствует вполне определенное значение другой (например, скорость свободного падения тела в вакууме в зависимости от времени и т.п.).
В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая зависимость получила название статистической (или с тохастической, вероятностной).
Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками. Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п.
В силу неоднозначности статистической зависимости между Y и X для исследователя, в частности, представляет интерес усредненная по x схема зависимости, т.е. закономерность в изменении условного математического ожидания МХ(Y) (математического ожидания случайной переменной Y, вычисленного в предположении, что переменная X приняла значение х в зависимости от х.
Определение. Корреляционной зависимостьюмежду двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Корреляционная зависимость может быть представлена в виде:
Мх(Y)=φ(x) (1) или МY(X)=φ(y) (2)
Уравнения (1) и (2) называются модельными уравнениями регрессии (или просто уравнениями регрессии) соответственно Y по X и X по Y, функции φ(х) и ψ(у) - модельными функциями регрессии (или функциями регрессии), а их графики — модельными линиями регрессии (или линиями регрессии).
Для отыскания модельных уравнений регрессии, вообще говоря, необходимо знать закон распределения двумерной случайной величины (Х,Y). На практике исследователь, как правило, располагает лишь выборкой пар значений (хi, уi) ограниченного объема. В этом случае речь может идти об оценке (приближенном выражении) по выборке функции регрессии. Такой наилучшей (в смысле метода наименьших квадратов) оценкой является выборочная линия (кривая) регрессии Y по X:
 (3)
(3)
где yх — условная (групповая) средняя переменной Y при фиксированном значении переменной Х= х; b0,b1…bp — параметры кривой.
Аналогично определяется выборочная линия (кривая) регрессии Х по Y:
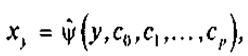 (4)
(4)
где ху — условная (групповая) средняя переменной X при фиксированном значении переменной Y = у; c0,c1,...,cp — параметры кривой.
Уравнения (3), (4) называют также выборочными уравнениями регрессии соответственно Y по X и X по Y.
Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа.
Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. Основной задачей корреляционного анализа — выявление связи между случайными переменными и оценка ее тесноты.
Линейная парная регрессия
Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.
Рассмотрим в качестве примера зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов X (млн руб.) для совокупности 50 однотипных предприятий (табл. 1).
В дальнейшем для краткости там, где это очевидно по смыслу, мы часто и выборочные уравнения (линии) регрессии будем называть просто уравнениями (линиями) регрессии.
(В таблице через хi и уj обозначены середины соответствующих интервалов, а ni и nj — соответственно их частоты).
Изобразим полученную зависимость графически точками координатной плоскости (рис. 1). Такое изображение статистической зависимости называется полем корреляции.
Для каждого значения хi (i = 1,2,...,l), т.е. для каждой строки корреляционной таблицы вычислим групповые средние
 (5)
(5)
где nij — частоты пар (хi, уj) и 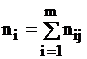 , m — число интервалов по переменной Y.
, m — число интервалов по переменной Y.
Таблица 1


Рис. 1
Вычисленные групповые средние  поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X (рис. 1).
поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X (рис. 1).
Аналогично для каждого значения yj (j = 1,2,...,m) по формуле
 (6)
(6)
вычислим групповые средние х, (см. нижнюю строку корреляционной таблицы), где  , l - число интервалов по переменной X.
, l - число интервалов по переменной X.
По виду ломаной можно предположить наличие линейной корреляционной зависимости Y по X между двумя рассматриваемыми переменными, которая графически выражается тем точнее, чем больше объем выборки (число рассматриваемых предприятий) п:
 (7)
(7)
Поэтому уравнение регрессии (3) будем искать в виде:
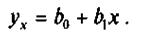 (8)
(8)
Найдем формулы расчета неизвестных параметров уравнения линейной регрессии. С этой целью применим метод наименьших квадратов, согласно которому неизвестные параметры Ь0 и Ь1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних  вычисленных по формуле (5), от значений
вычисленных по формуле (5), от значений  , найденных по уравнению регрессии (8), была минимальной:
, найденных по уравнению регрессии (8), была минимальной:
 (9)
(9)
На основании необходимого условия экстремума функции двух переменных S = S(Ь0, b1,) приравниваем нулю ее частные производные, т.е.

откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:
 (10)
(10)
Учитывая (5), преобразуем выражения:

Теперь с учетом (7), разделив обе части уравнений (10) на п, получим систему нормальных уравнений в виде:
 (11
(11
где соответствующие средние определяются по формулам:

Подставляя значение Ь0 =  - Ьx из первого уравнения системы (11) в уравнение регрессии (8), получим
- Ьx из первого уравнения системы (11) в уравнение регрессии (8), получим 
Коэффициент Ь1 в уравнении регрессии, называемый выборочным коэффициентом регрессии (или просто коэффициентом регрессии) У по X, будем обозначать символом Ьух. Теперь уравнение регрессии Y по X запишется так:

Коэффициент регрессии У по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.
Решая систему (12.11), найдем

где  — выборочная дисперсия переменной X:
— выборочная дисперсия переменной X:

μ — выборочный корреляционный момент или выборочная ковариация:
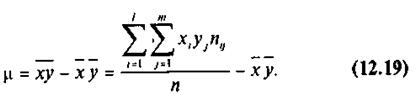
Рассуждая аналогично и полагая уравнение регрессии (4) линейным, можно привести его к виду:

— выборочный коэффициент регрессии (или просто коэффициент регрессии) X по Y, показывающий, на сколько единиц в среднем изменяется переменная X при увеличении переменной У на одну единицу,
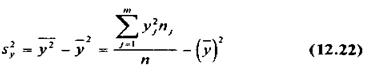
—выборочная дисперсия переменной Y.
Так как числители в формулах (17) и (21) для Ьyx и Ьxy совпадают, а знаменатели — положительные величины, то коэффициенты регрессии Ьyx и Ьxy, имеют одинаковые знаки, определяемые знаком μ. Из уравнений регрессии (16) и (20) следует, что коэффициенты Ьyx и 1/Ьxy определяют угловые коэффициенты (тангенсы углов наклона) к оси oх соответствующих линий регрессии, пересекающихся в точке ( ,
,  ) (см. рис. 3).
) (см. рис. 3).
Коэффициент корреляции
Перейдем к оценке тесноты корреляционной зависимости. Рассмотрим наиболее важный для практики и теории случай линейной зависимости вида (16).
На первый взгляд подходящим измерителем тесноты связи Y от X является коэффициент регрессии Ьуx ибо, как уже отмечено, он показывает, на сколько единиц в среднем изменяется Y, когда X увеличивается на одну единицу. Однако Ьуx зависит от единиц измерения переменных. Например, в полученной ранее зависимости он увеличится в 1000 раз, если величину основных производственных фондов X выразить не в млн руб., а в тыс. руб. Очевидно, что для «исправления» Ьуx как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Статистика знает такую систему единиц. Эта система использует в качестве единицы измерения переменной ее среднее квадратическое отклонение S.
Представим уравнение (16) в эквивалентном виде:
 (28)
(28)
В этой системе величина
 (29)
(29)
показывает, на сколько величин Sy изменится в среднем Y, когда Xувеличится на одно Sx Величина r является показателем тесноты связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).
На рис. 2 приведены две корреляционные зависимости переменной Y по X. Очевидно, что в случае а) зависимость между переменными менее тесная и коэффициент корреляции должен быть меньше, чем в случае б), так как точки корреляционного поля а) дальше отстоят от линии регрессии, чем точки поля б). Нетрудно видеть, что r совпадает по знаку с Ьуx (а значит, и с Ьху).

Рис. 2
Если r > 0 (Ьух>0, Ьху>0), то корреляционная связь между переменными называется прямой, если r < О (Ьуx<0, Ьху<0) — обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.
Учитывая (17), формулу для r представим в виде:

Отсюда видно, что формула для r симметрична относительно двух переменных, т.е. переменные Х и Y можно менять местами. Тогда аналогично (24) можно записать:

Найдя произведение обеих частей равенств (29) и (31), получим

т.е. коэффициент корреляции r переменных X и Y есть средняя геометрическая коэффициентов регрессии, имеющая их знак.



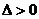 (по абсолютной величине), равна:
(по абсолютной величине), равна: , где
, где  (23)
(23) , где
, где 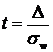 (24)
(24) - функция (интеграл вероятности) Лапласса
- функция (интеграл вероятности) Лапласса и выборочная доля
и выборочная доля  повторной выборки представляют сумму n независимых случайных величин
повторной выборки представляют сумму n независимых случайных величин  , где
, где 
 распределения
распределения  распределения
распределения 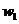 можно показать, что и в этом случае при
можно показать, что и в этом случае при 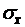 и выборочной доли
и выборочной доли  собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки.(Для бесповторной выборки обозначаем соответствено
собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки.(Для бесповторной выборки обозначаем соответствено 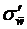 и
и  ).
).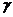 предельная ошибка выборки равна (-кратной величине средней квадра-тической ошибки, где
предельная ошибка выборки равна (-кратной величине средней квадра-тической ошибки, где 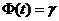 , т.е.
, т.е.
 (28), (27)
(28), (27) ,
, 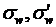 могут быть легко получены из формул (16), (17), (11), (12) соответствующих дисперсий
могут быть легко получены из формул (16), (17), (11), (12) соответствующих дисперсий  . Поместим их в таблицу:
. Поместим их в таблицу: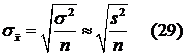

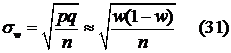

 неизвестны, то в формулах табл. 2 заменяем их состоятельными оценками по выборке — соответственно
неизвестны, то в формулах табл. 2 заменяем их состоятельными оценками по выборке — соответственно  , ибо при достаточно большом объеме выборки п практически достоверно, что
, ибо при достаточно большом объеме выборки п практически достоверно, что  .
. можно взять его максимально возможное значение
можно взять его максимально возможное значение 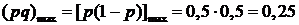 , (так как
, (так как  то рq максимально при р = 0,5).
то рq максимально при р = 0,5). и точность (предельную ошибку выборки)
и точность (предельную ошибку выборки) 
 откуда
откуда  , где
, где  . Аналогично могут быть получены и другие формулы объема выборки, которые сведем в таблицу:
. Аналогично могут быть получены и другие формулы объема выборки, которые сведем в таблицу:
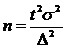
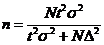
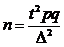
 , (37)
, (37) , то при одних и тех же точности и надежности оценок объем бесповторной выборки n всегда меньше объема повторной выборки
, то при одних и тех же точности и надежности оценок объем бесповторной выборки n всегда меньше объема повторной выборки  . Этим и объясняется тот факт, что на практике в основном используется бесповторная выборка.
. Этим и объясняется тот факт, что на практике в основном используется бесповторная выборка.
 или
или  (или)
(или)  .
.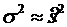 или
или 
 и надежности
и надежности  , либо объем бесповторной выборки значительно меньше объема генеральной совокупности
, либо объем бесповторной выборки значительно меньше объема генеральной совокупности  , расчеты средних квадратических ошибок (для средней и доли) и необходимого объема бесповторной выборки следует проводить по соответствующим формулам для повторной выборки.
, расчеты средних квадратических ошибок (для средней и доли) и необходимого объема бесповторной выборки следует проводить по соответствующим формулам для повторной выборки. Вместо точной
Вместо точной 
 . (38)
. (38) , (39)
, (39) заключена между 0 и 1, то область
заключена между 0 и 1, то область  нужно еще ограничить слева и справа прямыми
нужно еще ограничить слева и справа прямыми  (наличие «лишних» областей, выходящих за полосу
(наличие «лишних» областей, выходящих за полосу  , объясняется тем, что при значениях р, близких к 0 или 1. допущение о нормальном законе распределения
, объясняется тем, что при значениях р, близких к 0 или 1. допущение о нормальном законе распределения  для р определяются как точки пересечения соответствующей вертикальной прямой с эллипсом (рис. 2). Чем больше объем выборки п, тем «доверительный эллипс» более вытянут, тем уже доверительный интервал.
для р определяются как точки пересечения соответствующей вертикальной прямой с эллипсом (рис. 2). Чем больше объем выборки п, тем «доверительный эллипс» более вытянут, тем уже доверительный интервал.
 , (40)
, (40) (по сравнению с 1),
(по сравнению с 1),  (по сравнению с
(по сравнению с  (по сравнению с
(по сравнению с  можно пренебречь, и получим:
можно пренебречь, и получим:
 (3)
(3)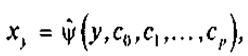 (4)
(4) (5)
(5)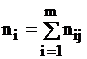 , m — число интервалов по переменной Y.
, m — число интервалов по переменной Y.

 поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X (рис. 1).
поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X (рис. 1). (6)
(6) , l - число интервалов по переменной X.
, l - число интервалов по переменной X. (7)
(7)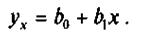 (8)
(8) вычисленных по формуле (5), от значений
вычисленных по формуле (5), от значений  , найденных по уравнению регрессии (8), была минимальной:
, найденных по уравнению регрессии (8), была минимальной: (9)
(9)
 (10)
(10)
 (11
(11
 - Ьx из первого уравнения системы (11) в уравнение регрессии (8), получим
- Ьx из первого уравнения системы (11) в уравнение регрессии (8), получим 


 — выборочная дисперсия переменной X:
— выборочная дисперсия переменной X:
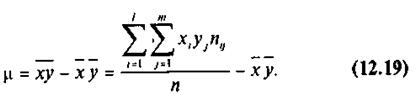

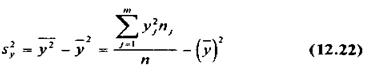
 ) (см. рис. 3).
) (см. рис. 3). (28)
(28) (29)
(29)





