Матричные игры с нулевой суммой

Матричная игра (с нулевой суммой) – это антагонистическая игра, в которой первый игрок А использует возможные стратегии , , …, , 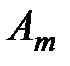а его противник (оппонент В) – стратегии , , …, 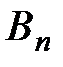. Если игрок А применит стратегию , а оппонент – стратегию , то плата игры будет выигрышем игрока А (проигрышем В) для и таким образом, игра с нулевой суммой полностью описывается так называемой платежной матрицей игры

Игроки	Стратегии игрока В
В А		…		…
Стра-тегии игрока А			…		…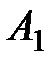
…	…………………………….
		…		…
…	…………………………….
		…		…

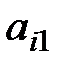
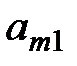
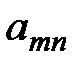
Если игра состоит только из личных ходов, то выбор пары чи­стых стратегий единственным образом определяет ис­ход (результат) игры. Если же в игре используются случай­ные ходы, то исход игры определяется средним значением (математическим ожиданием) выигрыша. Платежная матрица яв­ляется табличной записью функции выигрыша. В теории матричных игр всегда предполагается, что в платежной мат­рице записаны выигрыши игрока А.

При поиске оптимальных стратегий игроки опираются на основной принцип теории игр – принцип гарантированного результата – принцип максимина, в соответствии с которым каждый игрок, считая партнера по игре разумным противником, выбирает свои действия в предположении, что соперник не упустит возможности использовать в своих интересах любую его ошибку.

Выбирая свой ход игрок А анализирует платежную матрицу, определяя для своей каж­дой чистой стратегии () минималь­ное значение ожидаемого выигрыша: , , (считая, что противник играет наилучшим образом), и а затем из всех игрок А выберет наибольшее , и таким образом, выберет соответствующую ему чистую – максиминную – стратегию . Игрока А гарантирует себе выигрыш не хуже 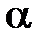при любых стратегиях игрока В и не существует чистой стратегии игрока А, которая давала бы ему больший выигрыш, чем 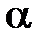при всех стратегиях игрока В.

Число 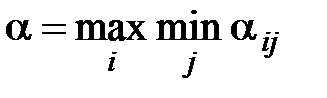называется нижней чистой ценой игры (максимином). Она выражает выигрыш игрока А, при использовании максиминной стратегии независимо от действий игрока В.

Число β определяемое по формуле,

называется верхней чистой ценой игры (минимаксом). Она показывает, какой максимальный проигрыш (гарантированный результат) может быть у игрока В при подходящем выборе им своей чистой стратегии (независимо от действий игрока А). Соответствующая стратегия игрока В называется минимаксной.

С тратегии (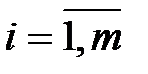) первого игрока и стратегии второго игрока (возможные их ходы) принято называть чистыми стратегиями.

Пример. Пусть первый игрок имеет т, а второй – п чистых стра­тегий, тогда каждую пару чистых стратегий первого и второго игро­ков можно представить в виде единичных векторов:

, ,

-е место -е место

Теорема. В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т. е. .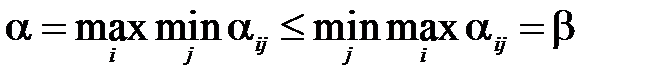

Если для чистых стратегий , игроков А и В соответ­ственно имеет место равенство , то пару чистых стра­тегий (, ) называют седловой точкой матричной игры, элемент , матрицы, стоящий на пересечении -й строки и -го столбца, – седловым элементом платежной матрицы, а число – чистой ценой игры.

Ситуация, когда ни один из игроков не имеет разумных оснований для изменения своей стратегии, называется ситуацией равновесия.

Если матричная игра имеет седловую точку, т.е. в платежной матрице присутствует элемент, который является одновременно минимальным в строке и максимальным в столбце, то она решается в чистых стратегиях. Чистые стратегии , , образующие седловую точку и будут оптимальными, а решением игры считается трой­ка объектов .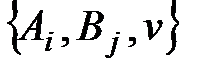

Про игры с седловой точкой говорят, что они решаются в чистых стратегиях, так как последние полностью определяют рациональное поведение конфликтующих сторон. Платежная матрица может иметь несколько седловых точек.

(Пример).Игра задана следующей платежной матрицей

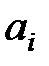
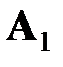
						1
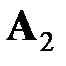
			-3		-1	-3
	7	4		5	6

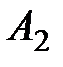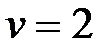– максиминная стратегия, – минимаксная стратегия, следовательно, и . Особенность этого примера в том, что если оппонент придерживается стратегии , то игроку А невыгодно использовать какую-либо стратегию кроме . Но если игрок А использует стратегию , то оппоненту придется использовать . Причина состоит в том, что выигрыш одновременно является минимальным для максиминной стратегии и максимальным для минимаксной стратегия 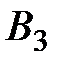. Это игра с седловой точкой , стратегии сторон , , соответствующие этой точке, являются оптимальными чистыми стратегиями. Чистая цена игры равна .

Пример. Игра задана следующей платежной матрицей

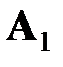
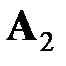
				-3
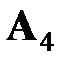
					-6

то для определения нижней и верхней чистой цены игры следует определить, какой выигрыш гарантирует игроку А каждая из стратегий при самых неблагоприятных действиях оппонента. Это означает, что в каждой строке нужно найти минимальное значение .

Поскольку оппонент может провести такой же анализ для выбора одной из стратегий , то в каждом столбце он будет искать максимально возможные значения выигрыша игрока А: . Дополняя платежную матрицу этими значениями, получим:

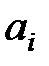
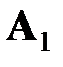
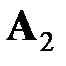
				-3			-3
							1
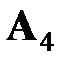
					-6		-6
	7	9		6	6	7

Из этой таблицы видно, что выбор стратегии гарантирует игроку А выигрыш не менее 4 ед. при любой стратегии оппонента. Таким образом, – максминая стратегия. Соответствующее ей значение 4 ед. – есть нижняя цена игры.

Для оппонента стратегия минимизирует максимально возможный проигрыш и называется минимаксной. Используя ее, оппонент не может проиграть больше верхней цены игры . Для рассматриваемого примера .

Смешанной стратегией p первого (А) игрока называется вектор

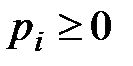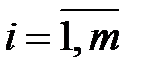, где , () и /

Аналогично q – смешанная стратегия игрока В:

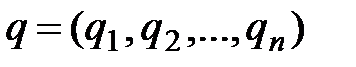(, где , () и ).

Здесь и – вероятности, с которыми игроки А и В выбирают свои чистые стратегии и в ходе игры.

Чистая стратегия игрока А может рассматриваться как частный случай смешанной стратегии, i -я компонента которой равна 1, а остальные равны 0. Аналогично для игрока В.

Применяя смешанные стратегии игроки выбирают свои чистые стратегии слу­чайно и независимо друг от друга и, таким образом, случайной становится величина выигрыша (про­игрыша):

– плата – платежная функция игры с платежной матрицей .

Смешанныестратегии , 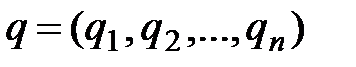называ­ются оптимальными, если для произвольных стратегий , 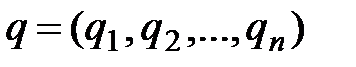выполняется условие

,

т.е. – является седловой точкой функции .

Использование в игре оптимальных смешанных стратегий обеспечивает первому игроку выигрыш, не меньший, чем при использовании им любой другой стратегии р, второму игро­ку – проигрыш, не больший, чем при использовании им лю­бой другой стратегии q.

Значение платежной функции при оптимальных стратеги­ях определяет цену игры v, т. е. , причем . Совокупность оптимальных стратегий и цены игры соста­вляет решение игры.

Теорема о минимаксе. В смешанных стратегиях любая конечная матричная игра имеет седловую точку, причем где – оптимальные смешанные стратегии игроков А и В соответственно.

Чистые стратегии игрока, входящие в его оптимальную смешанную стратегию с вероятностями, отличными от нуля, называются активными стратегиями игрока.

Решение игры можно существенно упростить, если своевременно выявить имеющееся в платежной матрице доминирование одних стратегий над другими, ибо это позволит предварительно сократить размеры матрицы.

Игрок А заинтересован в максимизации выигрыша. Поэтому в платежной матрице сравниваем элементы строк s и t, а именно: 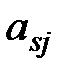с элемен­тами 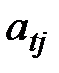для 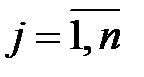. Если (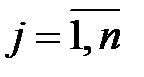) то выигрыш игрока А при стратегии будет больше, чем при стратегии , какую бы чистую стратегию не применил игрок В. В этом случае стратегия доминирует над стратегией . Стратегию называют доминирующей, а стратегию – доминируемой.

Поскольку игрок В заинтересован в минимизации про­игрыша, доминирующим будет столбец с наименьшими эле­ментами. Например, сравниваем элементы 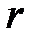-го и 1- го столбцов: если , , то игроку В выгодно выбрать стратегию , которая доминирует над стратегией . Стратегия называется доминирующей, а стратегия – доминируемой.

Если в матричной игре имеем строки (столбцы) с одними и теми же элементами, то такие строки (столбцы), а соответственно и стратегии игроков А и В называются дублирующими.

В матричной игре доминируемые и дублирующие строки (столбцы) можно опускать, что не влияет на решение игры, но позволяет уменьшить размерность платежной матрицы. Таким образом, если стратегия доминирует над стратегией , то вероятность применения последней в оп­тимальной смешанной стратегии р * игрока А равна нулю, а поэтому t -ю строку из платежной матрицы можно исключить. Если l -я стратегия игрока В доминирует над r -й стратегией , то r -й столбец из платежной матрицы можно исключить.

Пример. Можно упростить платежную мат­рицу, прибавляя, например, ко всем элементам достаточно боль­шое положительное число, в результате чего можно получить новую матрицу с положительными (неотрицательными) эле­ментами. Умножая элементы на подходящий положительный множитель (отличный от нуля), можно уменьшить (увеличить) элементы новой матрицы, что облегчает дальнейшие вычисле­ния. При этом вероятности активных стратегий не меняются.

Так, разделив элементы матрицы

на 100 (умножив на 0,01), а затем прибавив к элементам но­вой матрицы число 3, придем к матрице

.

Работать с этой матрицей проще, чем с исход­ной.

Поскольку оптимальные смешанные стратегии игроков в результате рассмотренных упрощений платежной матрицы не меняются, то все получаемые в процессе преобразований мат­рицы называют эквивалентными.

Решение матричных игр 2×2

Игра 2×2 является наиболее простым случаем конечных матричных игр. В этой игре каждый из игроков обладает только двумя стратегиями.

Рассмотрим матричную игру 2×2:

	В 1	В 2
А 1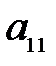
А 2

Если игра 2×2 имеет седловую точку, то ее решение очевидно.

Предположим, что игра не имеет седловой точки, т.е. . Требуется найти оптимальные смешанные стратегии игроков и , а также цену игры .

Очевидно, что в игре 2×2, не имеющей седловой точки, обе стратегии игроков являются активными. Поэтому если игрок A, будет применять свою оптимальную смешанную стратегию, то, независимо от действий игрока В, выигрыш его будет равен цене игры .

Игрок А будет применять стратегию А ₁ с вероятностью и стратегию А ₂ с вероятностью . Если игрок В отвечает своей стратегией В ₁, то выигрыш игрока А определяется из уравнения

.

Если же игрок В будет применять стратегию В ₂, то выигрыш игрока А не изменится и определяется равенством

.

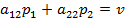Учитывая условие , получим систему трех уравнений с тремя неизвестными

Решив эту систему, найдем оптимальное решение для игрока А: и цену игры .

Аналогично определяется оптимальная стратегия игрока В из системы уравнений:

Таким образом, матричная игра сведена к системе линейных уравнений.

Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии. Рассмотрим игру (2× n).

	Второй игрок
			...
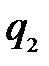
Первый игрок				...
			...

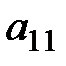
Предполагаем, что игра не имеет седловой точки. Обозначим: – вероятность применения первым игроком 1-й стратегии, – вероятность применения первым игроком 2-й стратегии, причем , – вероятность примене­ния вторым игроком 1-й стратегии, 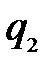– вероятность приме­нения вторым игроком 2-й стратегии и т.д., – вероятность применения вторым игроком n -й стратегии.

Ожидаемый выигрыш первого игрока при применении вто­рым игроком 1-й стратегии составит

Аналогично найдем ожидаемые выигрыши первого игрока при применении вторым игроком 2, 3,..., n -й стратегий. Полу­ченные данные поместим в таблицу.

Чистые стратегии второго игрока	Ожидаемые выигрыши первого игрока
...	...
n

Из таблицы видно, что ожидаемый выигрыш первого иг­рока линейно зависит от . На плоскости построим графики ожидаемых выигрышей первого игрока, которые представляют прямые, проходящие через точки и , .

Первый игрок должен выбирать такие стратегии, чтобы максимизировать свой минимальный ожидаемый выигрыш. Поэтому оптимальная стратегия первого игрока определяется как точка пересечения прямых, максимизирующих его мини­мальный ожидаемый выигрыш. Поскольку игрок А может рассчитывать только на выигрыш , то на плоскости рисуем график зависимости 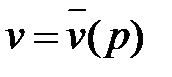и находим наивысшую точку 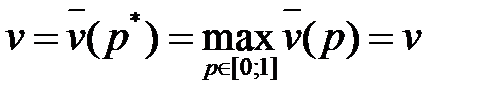на этом графике, ордината которой выражает цену игры , а стратегия является оптимальной смешанной стратегией игрока А.

Аналогично определяется оптимальная стратегия второго иг­рока. Она определяется как точка пересечения прямых, минимизирующих его максимальные ожидаемые проигрыши.

Статистические игры

Под статистической игрой (игрой с природой) будем понимать парную матричную игру, в которой один игрок заинтересован в наиболее выгодном для него исходе игры, а второй игрок («природа») безразличен к результату игры.

В отличие от матричных игр, в которых участвует два игрока, с противоположными интересами (один игрок старается максимизировать плату, а другой – минимизировать), в реальных задачах, приводящихся к игровым, зачастую имеется не­определенность, вызванная отсутствием информации об усло­виях, в которых осуществляется действие (погода, покупатель­ский спрос и т.д.) и эти условия не зависят от сознательных действий другого игрока. Такие игры относят к играм с природой. Сознательный игрок в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос и т.д.) действует случайно.

Предположим, что в игре с природой сознательный игрок А может использовать чистых стратегий , ,…, , а природа П может реализовать 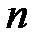различных состояний , ,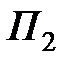…, . Игроку А могут быть известны вероятности ,…, , с которыми природа реализует свои состояния, но он может и не знать их.

Действуя против природы, игрок А имеет возможность использовать как чистые стратегии , так и смешанные стратегии. Если игрок А в состоянии оценить (величиной ) последствия применения каждой своей чистой стратегии при каждом состоянии природы, то игру можно задать матрицей:

= ,

которая называется платежной.

Решение статистической игры состоит из следующих этапов:

1. Выявление и отбрасывание дублирующих и доминируемых стратегий лица, играющего с природой; стратегии природы отбрасывать нельзя.

2. Построить и исследовать матрицу рисков.

3. Оценить выигрыш при различных игровых ситуациях: критерии Вальда, Байеса, Сэвиджа и Гурвица и др.;

4. Сделать вывод о выборе наилучшей стратегии.

Игры с природой, хотя и являются частным случаем парных матричных игр, обладают и некоторыми особенностями. Например, при упрощении платежной матрицы отбрасывать те или иные состояния природы нельзя, так как она может реализовать любое состояние независимо от того, выгодно оно игроку А или нет. Кроме того, решение достаточно найти только для игрока А, поскольку природа в рекомендациях «не нуждается».

Также в играх с природой смешанные стратегии имеют ограниченное значение: они приобретают смысл только при многократном повторении игры.

Таким образом, цель при решении статистической игры заключается в определении такой стратегии сознательного игрока (чистой или смешанной), которая при ее применении обеспечила бы наибольший выигрыш.

Риском игрока А, когда он пользуется чистой стратегией при состоянии природы, называется разность между максимальным выигрышем, который он мог бы получить, если бы точно знал, что природой будет реализовано именно состояние , и тем выигрышем, который он получит, используя стратегию:

,

где ― максимальный элемент -го столбца платежной матрицы. Элементы матрицы рисков, соответствующие стратегиям и характеризуют общую благоприятность или неблагоприятность для игрока А отдельных состояний природы. Матрица рисков имеет вид:

	П1	П2	...	Пn
A1
A2
…
Am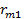

Для принятия решений в статистических играх используются следующие критерии:

1. Критерий, основанный на известных вероятностях условий, критерий Байеса. Пусть известны вероятности состояний природы, тогда пользуются критерием Байеса, в соответствии с которым оптимальной считается чистая стратегия , при которой максимизируется средний выигрыш . Следует отметить, что в этом случае игроку нет смысла пользоваться смешанными стратегиями. Применение в игре с природой в этом случае любой смешанной стратегии не увеличивает выигрыш игрока А, получаемый при оптимальной чистой стратегии.

2. Принцип недостаточного основания Лапласа. Если объективные оценки состояний природы получить невозможно, то вероятности состояний природы могут быть оценены субъективно на основе принципа недостаточного основания Лапласа, согласно которому все состояния природы полагаются равновероятными, т.е. , и оптимальной считают чистую стратегию , обеспечивающую максимальное среднее значение выигрыша: .

3. Максминный критерий Вальда. По этому критерию рекомендуется применять максиминную стратегию. Она достигается из условия , , , и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для сознательного игрока образом.

4. Критерий максимума. Оптимальная стратегия выбирается из условия 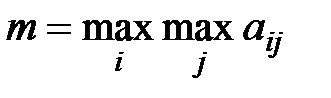, , . Критерий является оптимистическим, считается, что при­рода будет играть наиболее благоприятно для сознательного игрока.

5. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле , , , где (степень оптимизма) изменяется в диапазоне [0,1].

Критерий придерживается некоторой промежуточной по­зиции, учитывающей возможность как наихудшего, так и наи­лучшего поведения природы. При =1 критерий превращает­ся в критерий Вальда; при =0 — в критерий максимума. На оказывает влияние степень ответственности лица, принима­ющего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем ближе к единице. В общем случае число выбирают из опыта или субъективных соображений.

6. Критерий Сэвиджа. Суть критерия состоит в выборе та­кой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Согласно этому критерию, рекомендуется выбирать ту стратегию, при которой в наихудших условиях величина риска принимает наименьшее значение: – оптимальная стратегия, где - элементы матрицы рисков.

 

Элементы сетевого планирования

Современное сетевое планирование начинается с разбиения программы работ на операции. Определяются оценки продол­жительности операций, и строится сетевая модель (график). Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала ее реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Календарный график выявляет критические операции, которым надо уделять особое внима­ние, чтобы закончить все работы в директивный срок. Что касается некритических операций, то календарный план поз­воляет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффектив­ном применении как трудовых, так и финансовых ресурсов.

Сетевая модель — графическое изображение плана выпол­нения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций.

Работа — это любые операции, трудовые процессы, сопровождающиеся затратами ресурсов или времени. Это активный процесс, требующий затрат ресур­сов, либо пассивный (ожидание), приводящий к достижению намеченного результата. На сетевых графиках работы изображают стрелками. Рядом со стрелкой указываются числовые характеристики: время выполнения работы, расход ресурса, количество исполнителей и т. д. Под работами подразумеваю