

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
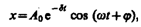
где частота  (см. (146.4)).Добротность пружинного маятника, согласно (146.8) и (146.10), Q=
(см. (146.4)).Добротность пружинного маятника, согласно (146.8) и (146.10), Q=  /r
/r
Вопрос 10 Свободные затухающие колебания в электрическом колебательном контуре. Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R¹ 0) имеет вид (см. (143.2))
 Учитывая выражение (143.4) и принимая коэффициент затухания
Учитывая выражение (143.4) и принимая коэффициент затухания  (146.11)дифференциальное уравнение (143.2) можно записать в идентичном уравнению (146.1) виде
(146.11)дифференциальное уравнение (143.2) можно записать в идентичном уравнению (146.1) виде

Из выражений (146.1) и (146.5) вытекает, что колебания заряда совершаются по закону  (146.12)с частотой, согласно (146.4),
(146.12)с частотой, согласно (146.4),  (146.13)меньшей собственной частоты контура w 0 (см. (143.4)). При R= 0 формула (146.13) переходит в (143.4).Логарифмический декремент затухания определяется формулой (146.7), а добротность колебательного контура (см. (146.8))
(146.13)меньшей собственной частоты контура w 0 (см. (143.4)). При R= 0 формула (146.13) переходит в (143.4).Логарифмический декремент затухания определяется формулой (146.7), а добротность колебательного контура (см. (146.8))  (146.14)
(146.14)
В заключение отметим, что при увеличении коэффициента затухания d период затухающих колебании растет и при d=w 0 обращается в бесконечность, т. е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t ®¥. Процесс не будет колебательным. Он называется апериодическим.
Огромный интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы так называемые автоколебания — незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.
Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний (см. § 147), происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).
|
|
Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй.
Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т. д.
Вопрос 11 Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение
Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X (t), изменяющего по гармоническому закону:  Если рассматривать механические колебания, то роль X (t) играет внешняя вынуждающая сила
Если рассматривать механические колебания, то роль X (t) играет внешняя вынуждающая сила  (147.1)С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде
(147.1)С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде  используя (142.2) и (146.10), придем к уравнению
используя (142.2) и (146.10), придем к уравнению  (147.2)Если рассматривать электрический колебательный контур, то роль X (t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение
(147.2)Если рассматривать электрический колебательный контур, то роль X (t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение  (147.3)Тогда уравнение (143.2) с учетом (147.3) можно записать в виде
(147.3)Тогда уравнение (143.2) с учетом (147.3) можно записать в виде  Используя (143.4) и (146.11), придем к уравнению
Используя (143.4) и (146.11), придем к уравнению  (147.4)Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.
(147.4)Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.
Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференциальному уравнению  147.5)применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x 0 в случае механических колебаний равно F 0 /m, в случае электромагнитных — U m/ L).
147.5)применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x 0 в случае механических колебаний равно F 0 /m, в случае электромагнитных — U m/ L).
|
|
Решение уравнения (147.5) равно сумме общего решения (146.5) однородного уравнения (146.1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме (см. § 140). Заменим правую часть уравнения (147.5) на комплексную величину х 0  :
:  147.6)Частное решение этого уравнения будем искать в виде
147.6)Частное решение этого уравнения будем искать в виде  Подставляя выражение для s и его производных
Подставляя выражение для s и его производных  в уравнение (147.6), получаем
в уравнение (147.6), получаем  (147.7)
(147.7)
Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h=w. Учитывая это, из уравнения (147.7) найдем величину s 0 и умножим ее числитель и знаменатель на 
 Это комплексное число удобно представить в экспоненциальной форме:
Это комплексное число удобно представить в экспоненциальной форме:  где
где  (147.8)
(147.8)  (147.9)
(147.9)
Следовательно, решение уравнения (147.6) в комплексной форме примет вид  Его вещественная часть, являющаяся решением уравнения (147.5), равна
Его вещественная часть, являющаяся решением уравнения (147.5), равна  (147.10) где А и j задаются соответственно формулами (147.8) и (147.9).Таким образом, частное решение неоднородного уравнения (147.5) имеет вид
(147.10) где А и j задаются соответственно формулами (147.8) и (147.9).Таким образом, частное решение неоднородного уравнения (147.5) имеет вид  (147.11)Решение уравнения (147.5) равно сумме общего решения однородного уравнения
(147.11)Решение уравнения (147.5) равно сумме общего решения однородного уравнения  (147.12)(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.
(147.12)(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.  Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что
Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что  (см. (143.4)) и
(см. (143.4)) и  (см. (146.11)):
(см. (146.11)):  (147.13)
(147.13)
Продифференцировав Q=Q mcos(wt–a) по t, найдем силу тока в контуре при установившихся колебаниях:  (147.14)где
(147.14)где  (147.15)
(147.15)
Выражение (147.14) может быть записано в ввде  где j = a – p /2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)
где j = a – p /2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)  (147.16)Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (j> 0), если wL> 1/(w С), и опережает напряжение (j< 0), если wL< 1/(w С).
(147.16)Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (j> 0), если wL> 1/(w С), и опережает напряжение (j< 0), если wL< 1/(w С).
Формулы (147.15) и (147.16) можно также получить с помощью векторной диаграммы. Это сделано в §149 для переменных токов.
|
|
Вопрос 12 Амплитуда и фаза вынужденных колебаний (механических и электромагнитных). Резонанс
Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты w. Механические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.
Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту w рез, — частоту, при которой амплитуда А смещения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по w и приравняв его нулю, получим условие, определяющее w рез:
 Это равенство выполняется при w =0, ±
Это равенство выполняется при w =0, ± 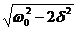 , у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота
, у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота  (148.1) Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При
(148.1) Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При  значение w рез практически совпадает с собственной частотой w 0 колебательной системы. Подставляя (148.1) в формулу (147.8), получим
значение w рез практически совпадает с собственной частотой w 0 колебательной системы. Подставляя (148.1) в формулу (147.8), получим 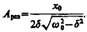 (148.2) На рис. 210 приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях d. Из (148.1) и (148.2) вытекает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w ® 0, то все кривые (см. также (147.8)) достигают одного в того же, отличного от нуля, предельного значения
(148.2) На рис. 210 приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях d. Из (148.1) и (148.2) вытекает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w ® 0, то все кривые (см. также (147.8)) достигают одного в того же, отличного от нуля, предельного значения  , которое называют статическим отклонением. В случае механических колебаний
, которое называют статическим отклонением. В случае механических колебаний 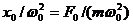 , в случае электромагнитных – U m / (L
, в случае электромагнитных – U m / (L  ). Если w ®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.
). Если w ®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Из формулы (148.2) вытекает, что при малом затухании ( ) резонансная амплитуда смещения (заряда)
) резонансная амплитуда смещения (заряда)  где Q — добротность колебательной системы (см. (146.8)),
где Q — добротность колебательной системы (см. (146.8)),  — рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А рез.
— рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А рез.
|
|
На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока)  максимальна при w рез =w 0 и равна
максимальна при w рез =w 0 и равна  , т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна
, т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна  а амплитуда тока при электрическом резонансе
а амплитуда тока при электрическом резонансе  Из выражения tg j =
Из выражения tg j =  (см. (147.9)) следует, что если затухание в системе отсутствует (d= 0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹0.
(см. (147.9)) следует, что если затухание в системе отсутствует (d= 0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹0.
Зависимость j от w при разных коэффициентах d графически представлена на рис. 212, из которого следует, что при изменении w изменяется и сдвиг фаз j. Из формулы (147.9) вытекает, что при w =0 j =0, а при w = w 0 независимо от значения коэффициента затухания j = p /2, т. е. сила (напряжение) опережает по фазе колебания на p /2. При дальнейшем увеличении w сдвиг фаз возрастает и при w >> w 0 j ® p, т. е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.
Вопрос 13 Волновые процессы. Продольные и поперечные волны
Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерывно распределенная в пространстве и обладающая упругими свойствами.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
|
|
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением x частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Приведенный график функции x (x, t)похож на график гармонического колебания, однако они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний — зависимость смещения данной частицы от времени.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.

или, учитывая, что T = 1/ n, где n — частота колебаний,


Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени — один. Волновой фронт также является волновой поверхностью. Волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.
Вопрос 14 Уравнение бегущей волны. Фазовая скорость. Волновое уравнение
Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846—1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.
Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис. 220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от x и t, т. е. x = x (x, t).
На рис. 220 рассмотрим некоторую частицу В среды, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х= 0,описываются функцией x (0, t) = A cos wt, то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на t, так как для прохождения волной расстояния х требуется время t = x / v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид  (154.1) откуда следует, что x (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то
(154.1) откуда следует, что x (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то  В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид  (154.2)где А = const — амплитуда волны, w — циклическая частота, j 0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, [ w (t—x/v)+ j 0] — фаза плоской волны.Для характеристики волн используется волновое число
(154.2)где А = const — амплитуда волны, w — циклическая частота, j 0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, [ w (t—x/v)+ j 0] — фаза плоской волны.Для характеристики волн используется волновое число 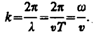 (154.3)Учитывая (154.3), уравнению (154.2) можно придать вид
(154.3)Учитывая (154.3), уравнению (154.2) можно придать вид  (154.4)Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде
(154.4)Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде 
где физический смысл имеет лишь действительная часть (см. § 140). Предположим, что при волновом процессе фаза постоянна, т. е.  (154.5)Продифференцировав выражение (154.5) и сократив на w, получим
(154.5)Продифференцировав выражение (154.5) и сократив на w, получим  откуда
откуда  (154.6)Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.
(154.6)Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.
Вопрос 17 Принцип суперпозиции. Групповая скорость
Если среда, в которой распространяется одновременно несколько волн, линейна, т. е. ее свойства не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения) волн: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Исходя из принципа суперпозиции и разложения Фурье (см. (144.5)) любая волна может быть представлена в виде суммы гармонических волн, т. е. в виде волнового пакета, или группы волн. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.
«Сконструируем» простейший волновой пакет из двух распространяющихся вдоль положительного направления оси х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем d w << w и d k<<k. Тогда  Эта волна отличается от гармонической тем, что ее амплитуда
Эта волна отличается от гармонической тем, что ее амплитуда  есть медленно изменяющаяся функция координаты х и времени t. За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что t d w —x d k = const, получим
есть медленно изменяющаяся функция координаты х и времени t. За скорость распространения этой негармонической волны (волнового пакета) принимают скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета. При условии, что t d w —x d k = const, получим  (155.1)
(155.1)
Скорость и есть групповая скорость. Ее можно определить как скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет. Выражение (155.1) получено для волнового пакета из двух составляющих, однако можно доказать, что оно справедливо в самом общем случае.Рассмотрим связь между групповой  (см. (155.1)) и фазовой v=w /k (см. (154.8)) скоростями. Учитывая, что k= 2 p/l (см. (154.3)), получим
(см. (155.1)) и фазовой v=w /k (см. (154.8)) скоростями. Учитывая, что k= 2 p/l (см. (154.3)), получим  или
или  (155.2)
(155.2)
Из формулы (155.2) вытекает, что u может быть как меньше, так и больше v в зависимости от знака d v/ d l. В недиспергирующей среде d v/ d l= 0 и групповая скорость совпадает с фазовой. Понятие групповой скорости очень важно, так как именно она фигурирует при измерении дальности в радиолокации, в системах управления космическими объектами и т. д. В теории относительности доказывается, что групповая скорость u << с, в то время как для фазовой скорости ограничений не существует.
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!