Движение тел с переменной массой. Уравнение Мещерского. Фолмула Циолковского.

Получим уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).

Пусть в момент времени t масса ракеты m, а ее скорость v; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины v+dv. Изменение импульса системы за время dt будет равно:

где u - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:

Если на систему действуют внешние силы, то или dp = Fdt. Тогда Fdt = mdv + udm, или (2.12) где член называют реактивной силой Fp. Если вектор u противоположен v, то ракета ускоряется, а если совпадает с v, то тормозится.

Таким образом, уравнение движения тела переменной массы имеет следующий вид: (2.13)

Уравнение (2.13) называется уравнением И.В. Мещерского.

Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая F = 0 и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим: откуда или где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени v=0, а стартовая масса ракеты составляет m0, то C = u*ln m0. Следовательно, (2.14)

Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:

а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m0;

б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.

Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости v и u намного меньше скорости света c.

28. Дифференциальное уравнение гаронических колебаний и его решение. Определение амплитуды и начальной фазы по начальным условиям. Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса: или гдеA - амплитуда; ω - круговая частота; α - начальная фаза; (ωt + α) - фаза.

Фаза колебания - это аргумент гармонической функции: (ωt + α). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0.

Амплитуда колебанияA - это наибольшее значение колеблющейся величины.

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π.

ω(t + T) +α = ωt + α + 2π, или ωT = 2π.

Время T одного полного колебания называется периодом колебания. Частотойν называют величину, обратную периоду

Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1. Так как то

Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем. Действительно:

График гармонического колебания:

Дифференциальное уравнение гармонических колебаний:

колебания грузика, прикрепленного к пружине

x - координата грузика

колебание физического маятника - любого тела, совершающего колебания вокруг горизонтальной оси, не проходящей через его центр тяжести

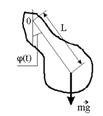
φ - угол отклонения

 

Мы получили дифференциальные уравнения, описывающие движения наших систем. В первых двух случаях уравнения одинаковы по форме, в третьем случае второй член уравнения содержит не φ, а Sin φ. Если рассматривать только малые отклонения маятника от положения равновесия, то тогда, при φ<< 1, Sin φ ≈ φи мы имеем:

Введем обозначения: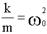

Решение дифференциального уравнения:

Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество. Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид: т.е. является гармонической функцией. Значит уравнение это дифференциальное уравнение гармонических колебаний.

Гармонический осциллятор. Примеры: Пружинный, математический, физический маятники.

Гармоническим осциллятором называется система, которая совершает колебания, описываемые выражением вида d2s/dt2 + ω02s = 0 или (1)

где две точки сверху означают двукратное дифференцирование по времени. Колебания гармонического осциллятора есть важный пример периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. В качестве примеров гармонического осциллятора могут быть пружинный, физический и математический маятники, колебательный контур (для токов и напряжений настолько малых, что можно было бы элементы контура считать линейными).

Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид или

Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой (2) и периодом (3)

Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна

Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела

физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом где введена величина L=J/(ml) — приведенная длина физического маятника.

Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника где l — длина маятника.

Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то

Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.