Ранее отмечалось, что теория вероятностей изучает закономерности массовых случайных явлений. Эти закономерности отражают устойчивость массовых случайных явлений. В широком смысле под устойчивостью понимается то, что при очень большом числе случайных явлений средний результат перестаёт быть случайным. В узком смысле под устойчивостью понимается ряд, в каждом из которых устанавливается факт приближения степени результатов опыта к некоторым определённым постоянным.
Другая группа теорем устанавливает условия, при которых наступает определённый закон распределения случайной величины.
Неравенство Чебышева
Неравенство Чебышева утверждает: каково бы ни было положительное число a, вероятность того, что случайная величина Х отклонится от математического ожидания на величину, большую или равную этому числу (числу a), ограничена сверху величиной  , т.е. справедливо неравенство:
, т.е. справедливо неравенство:  (1)
(1)
где  - математическое ожидание случайной величины;
- математическое ожидание случайной величины;  - дисперсия.
- дисперсия.
Доказательство: Приведём доказательство этого неравенства для дискретной случайной величины (оно здесь более наглядно). Представим дискретную случайную величину в виде точек на числовой оси:

На этой оси отложим точку, соответствующую математическому ожиданию, относительно которой отложим отрезки -a и a. Известно, что дисперсия дискретной случайной величины:
 (2)
(2)
Наряду с выражением (2) рассмотрим две суммы:
 (3)
(3)
 (4)
(4)
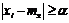 - это точки лежащие правее/левее отрезков -a и a.
- это точки лежащие правее/левее отрезков -a и a.
Из выражений (2), (3) и (4) можно записать систему неравенств:  (5)
(5)
Выражение (4) можно представить в виде:  (6)
(6)
Тогда можно записать неравенство в виде: 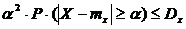 (7)
(7)
Отсюда следует: 
Аналогичным образом это неравенство можно доказать и для непрерывной случайной величины.
Частная теорема Чебышева
Эта теорема устанавливает связь между среднеарифметическим результатом наблюдений за случайной величиной и её математическим ожиданием. Пусть имеется некоторая случайная величина Х, над которой проводятся результаты наблюдений (опыт):  . При этом каждый из n опытов независим, а результат опыта рассматривается как случайная величина с характеристиками, соответствующими характеристикам исследуемой случайной величины, т.е. можно записать:
. При этом каждый из n опытов независим, а результат опыта рассматривается как случайная величина с характеристиками, соответствующими характеристикам исследуемой случайной величины, т.е. можно записать:
 (1)
(1)  (2)
(2)
Где  и
и  - соответственно математическое ожидание и дисперсия случайной величины Х.
- соответственно математическое ожидание и дисперсия случайной величины Х.
Известно, что среднеарифметическое результатов наблюдения определяется по формуле:  (3)
(3)
Т.е. среднеарифметическое результатов наблюдений представляет собой произведение неслучайной величины на сумму случайных величин с одинаковыми характеристиками.
Определим характеристики среднеарифметического результатов наблюдений.
Математическое ожидание будет равно:
 (4)
(4)
На основании теоремы о математическом ожидании произведения случайной величины на случайную и теоремы о математическом ожидании суммы случайных величин выражение (4) можно записать в виде:
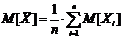 (5)
(5)
С учётом равенства (1) данное выражение также можно представить:  (6)
(6)
Таким образом, математическое ожидание среднеарифметического результатов наблюдений равняется математическому ожиданию случайной величины.
С учётом того, что случайные величины  независимы, и дисперсии этих случайных величин равны между собой, то на основании теоремы о дисперсии произведения неслучайной величины на случайную и теоремы о дисперсии суммы независимых случайных величин дисперсию среднеарифметического значения можно записать в виде:
независимы, и дисперсии этих случайных величин равны между собой, то на основании теоремы о дисперсии произведения неслучайной величины на случайную и теоремы о дисперсии суммы независимых случайных величин дисперсию среднеарифметического значения можно записать в виде:
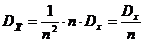 (7)
(7)
Таким образом, дисперсия среднеарифметического значения в n раз меньше дисперсии исследуемой случайной величины.
На основании выражений (6) и (7) Чебышевым была сформулирована теорема.
"Т" При достаточно большом числе независимых испытаний над случайной величиной Х среднеарифметическое результатов наблюдений сходится по вероятности к математическому ожиданию случайной величины Х.
Эта теорема в аналитическом виде задаётся выражением:  (8)
(8)
где  и
и  (дэльта) – сколь угодно малые, но конечные величины.
(дэльта) – сколь угодно малые, но конечные величины.
Доказательство: На основании неравенства Чебышева с учётом выражения (6) и (7) можно записать:
 (9)
(9)
Если от неравенства (9) на основании понятия о противоположном событии перейти к неравенству вида:
 (10)
(10)
то можно заметить, что для любого числа  (дэльта) можно подобрать такой объём выборки n, что будет выполняться условие:
(дэльта) можно подобрать такой объём выборки n, что будет выполняться условие:
 (11)
(11)
С учётом неравенства (11) неравенство (10) можно записать в виде:
 (12), что и требовалось доказать.
(12), что и требовалось доказать.
Общая теорема Чебышева
Данная теорема формулируется следующим образом:
"Т" Если случайные величины  независимы с математическими ожиданиями
независимы с математическими ожиданиями 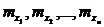 , в общем случае неравными друг другу, и дисперсиями
, в общем случае неравными друг другу, и дисперсиями  , также неравными друг другу, то максимальное значение дисперсии ограничено сверху некоторой величиной
, также неравными друг другу, то максимальное значение дисперсии ограничено сверху некоторой величиной  , тогда справедлива теорема:
, тогда справедлива теорема:
Среднеарифметическое результатов наблюдений над данной системой случайных величин сходится по вероятности к среднеарифметическому их математических ожиданий при неограниченном увеличении числа опытов над данной системой.
Данная теорема записывается в виде:
 (13) где
(13) где  и
и  (дэльта) – сколь угодно малые величины.
(дэльта) – сколь угодно малые величины.
Теорема Бернулли и Пуассона
Частным случаем теоремы Чебышева являются теоремы Бернулли и Пуассона.
Известно, что если проводится серия опытов, в каждом из которых событие может появиться с вероятностью Р, то статистической вероятностью данного события будет являться выражение:
 (1),
(1),
где n – число опытов,
m – число опытов, в которых появилось событие.
Теорема Бернулли утверждает:
"Т" При неограниченном увеличении числа опытов, в каждом из которых событие может появиться с вероятностью Р, статистическая частота этого события сходится по вероятности к вероятности появления события в отдельном испытании.
Данную теорему можно записать в виде:
 (2)где
(2)где  и
и  (дэльта) – сколь угодно малые, но конечные величины.
(дэльта) – сколь угодно малые, но конечные величины.
Доказательство: статистическую вероятность события можно представить в виде суммы случайных величин, делённой на число испытаний:
 (3)
(3)
При этом каждая из случайных величин независима от других (так как опыты независимы). Эти случайные величины имеют одно и то же распределение вида:
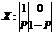 (
( )
)
Соответственно, характеристики каждой из случайных величин таковы:


На основании теорем о числовых характеристиках можем записать, что математическое ожидание статистической вероятности равняется:
 (4)
(4)
То есть математическое ожидание статистической вероятности равняется вероятности появления события в отдельном испытании.
На основании теоремы о дисперсии функции от случайных величин дисперсия статистической вероятности будет определяться выражением:
 (5)
(5)
С учётом характеристик статистической вероятности неравенство Чебышева можно записать в виде:
 (6)
(6)
Данное неравенство, выраженное через противоположное событие, будет иметь вид:
 (7)
(7)
Для любого  можно подобрать такое число наблюдений
можно подобрать такое число наблюдений 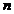 , что будет выполнено условие:
, что будет выполнено условие:
 , какое бы
, какое бы  ни было; (8)
ни было; (8)
тогда можно перейти к неравенству вида:
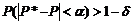 (9)
(9)
Если проводится 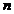 испытаний и в каждом испытании вероятности появления события различны, то в этом случае справедлива теорема Пуассона, утверждающая:
испытаний и в каждом испытании вероятности появления события различны, то в этом случае справедлива теорема Пуассона, утверждающая:
"Т" Если проводится 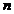 испытаний и в i -том испытании вероятность появления события равна
испытаний и в i -том испытании вероятность появления события равна  , то при неограниченном увеличении числа опытов
, то при неограниченном увеличении числа опытов 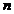 статистическая вероятность сходится по вероятности к среднеарифметическому вероятностей появления событий.
статистическая вероятность сходится по вероятности к среднеарифметическому вероятностей появления событий.
(Это вообщем-то частный случай общей теоремы Бернулли). Записывается эта теорема в виде:
 (10)
(10)



 , т.е. справедливо неравенство:
, т.е. справедливо неравенство:  (1)
(1) - математическое ожидание случайной величины;
- математическое ожидание случайной величины;  - дисперсия.
- дисперсия.
 (2)
(2) (3)
(3) (4)
(4)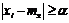 - это точки лежащие правее/левее отрезков -a и a.
- это точки лежащие правее/левее отрезков -a и a. (5)
(5) (6)
(6)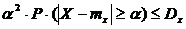 (7)
(7)
 . При этом каждый из n опытов независим, а результат опыта рассматривается как случайная величина с характеристиками, соответствующими характеристикам исследуемой случайной величины, т.е. можно записать:
. При этом каждый из n опытов независим, а результат опыта рассматривается как случайная величина с характеристиками, соответствующими характеристикам исследуемой случайной величины, т.е. можно записать: (1)
(1)  (2)
(2) (3)
(3) (4)
(4)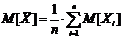 (5)
(5) (6)
(6)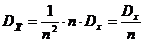 (7)
(7) (8)
(8) и
и  (дэльта) – сколь угодно малые, но конечные величины.
(дэльта) – сколь угодно малые, но конечные величины. (9)
(9) (10)
(10) (11)
(11) (12), что и требовалось доказать.
(12), что и требовалось доказать. независимы с математическими ожиданиями
независимы с математическими ожиданиями 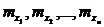 , в общем случае неравными друг другу, и дисперсиями
, в общем случае неравными друг другу, и дисперсиями  , также неравными друг другу, то максимальное значение дисперсии ограничено сверху некоторой величиной
, также неравными друг другу, то максимальное значение дисперсии ограничено сверху некоторой величиной  , тогда справедлива теорема:
, тогда справедлива теорема: (13) где
(13) где  (1),
(1), (2)где
(2)где  (3)
(3)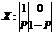 (
( )
)

 (4)
(4) (5)
(5) (6)
(6) (7)
(7)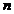 , что будет выполнено условие:
, что будет выполнено условие: , какое бы
, какое бы 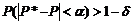 (9)
(9) , то при неограниченном увеличении числа опытов
, то при неограниченном увеличении числа опытов  (10)
(10)


