Свойства и отношения. Классификация отношений.
Как показывают исследования ряда естественных языков и различных предметных областей, существует конечное множество базовых отношений между информационными единицами и объектами реального мира, используя комбинации которых можно выразить необходимые отношения. Отношением называется взаимозависимость или взаимодействие двух или более объектов либо явлений абстрактного или конкретного типа.
Теоретико-множественные отношения позволяют сформировать классы понятий, а также упорядочить понятия в рамках этих классов. Этот вид взаимосвязей представляется отношениями «род-вид» и «часть-целое», которые используются для построения рабочей модели организации знаний, выражая свойство вложенности (наследственности) понятий.
Характеристические отношения «иметь свойство» и «иметь состояние» дают возможность описать объекты предметной области и процессы путем выделения наиболее существенных их характеристик и установить таким образом зависимости между объектами и свойствами, процессами и состояниями.
Каузальные отношения лежат в основе построения формальных логических рассуждений, которые могут использоваться для формирования маршрута проектирования, прогнозирования, анализа проектных ситуаций и т. д. Отношения «причина-следствие» связывают факты, между которыми существует причинно-следственная зависимость, например результат оценки свойства и последующий процесс. Отношения «влиять на» не отражают существование причинно-следственных зависимостей и определяют вероятность следствия при наличии причины. Этот вид каузальных отношений носит нечеткий характер и отражает неполноту знаний проектировщика.
Инструментальные отношения «выполняться посредством» связывают процессы и реализующие их процедуры. Необходимость разграничения понятий «процесс» и «процедура» обусловлена тем, что процесс может быть реализован посредством набора альтернативных процедур, различающихся временем выполнения, качеством получаемых результатов и т. д.
Квантифицирующие отношения позволяют установить соответствие между свойствами и их значениями. Поскольку значения могут быть как чи еловыми, так и лингвистическими, отношения этого вида представляются как «иметь числовое значение» и «иметь лингвистическое значение».
Временные отношения отражают относительное протекание процессов во времени. Они имеют вид «быть раньше», «быть позже», «быть одновременно» и дают возможность построения рабочих моделей, определяющих последовательности процессов в ходе проектирования.
Пространственные отношения характеризуют пространственное расположение объектов и определяют абсолютное расстояние между ними (отношение «расстояние между») или их взаиморасположение (отношение «быть расположенным»).
Арифметические отношения используются для построения вычислительных моделей для определения значений свойств и характеристик объектов и процессов.
Логические отношения служат связками при описании всех указанных функций и в этом смысле являются универсальными.
Логическая модель представления знаний. Декларативное и процедурное представление знаний. Система логического вывода (СЛВ).
Логические методы представления знаний базируются на использовании понятия формальной системы, задаваемой множеством базовых элементов, множеством синтаксических правил, позволяющих строить из базовых элементов синтаксически правильные выражения, множеством аксиом, множеством семантических правил вывода, позволяющих расширять множество аксиом за счет других выражений. Логические методы представления знаний обеспечивают единственность теоретического обоснования системы формально точных определений и выводов, простоту и ясность нотации для записи фактов, которая обладает четко определенной семантикой и простотой для понимания. В то же время основным недостатком логических методов является отсутствие четких принципов организации фактов в базе знаний, что затрудняет ее анализ и обработку. Это приводит к тому, что логические методы используются в основном в тех предметных областях, где система знаний невелика по объему и имеет однородную структуру.
При процедурном способе знания в основном представляются в форме процедур их использования. Преимущества процедурного представления сказываются в тех случаях, когда знания относятся в основном к операциям над объектами. Кроме того, процедурное представление обычно употребляется в системах вероятностного вывода и применительно к знаниям эвристического характера. При декларативном способе большинство знаний представляется как статический набор фактов в сочетании с небольшим количеством обобщенных процедур манипулирования ими. Преимущество декларативной схемы заключается в том, что каждый факт нужно хранить в единственном экземпляре, независимо от числа способов его использования. Кроме того, в этом случае проще добавлять новые факты, поскольку при этом не нужно менять все связанные с ними процедуры и подпрограммы.
Система логического вывода (СЛВ) - это средство управления рассуждениями. Логический вывод (ЛВ) сводится к упорядоченному раскфпию правил, которые определяются стратегией. Использование разных стратегий на данной модели дает разные результаты. На языке экспертных систем термин правило имеет более узкое значение, чем обычно. Это наиболее популярный способ представления знаний.
Правила обеспечивают формальный способ представления рекомендаций, указаний, стратегий. Правила часто возникают из эмпирических ассоциаций.
Знания в базе знаний представляются набором правил. Правила проверяются на группе фактов или знаний о текущей ситуации. Интерпретатор правил сопоставляет левые части правил (за словом «если») - посылки, с фактами правой части правил и выполняет то правило, посылка которого согласуется с фактами. Правила выражаются в виде утверждений «Если..., то...» или в виде импликаций. Действие правила может состоять в модификации набора фактов в базе знаний, например добавление нового факта. Новые факты, добавленные в базу знаний, могут сами быть использованы для сопоставления с левыми частями правил. Процесс сопоставления посылок правил с фактами может порождать цепочки выводов.
Существует два основных способа вывода: прямой и обратный. Цель прямого вывода - порождение данных на основе исходных данных и логических рассуждений. Цель обратного вывода - определение причин, т. е. фактов, которые привели к определенному результату (значению целевой функции).
Байесовские сети доверия.
Байесовская теория вероятностей обеспечивает математическую основу для рассуждения в условиях неопределенности. Однако сложность, возникающая при ее применении к реальным предметным областям, может оказаться недопустимой. Подход, называемый байесовскими сетями доверия (Bayesian Belief Network, БСД), предлагает вычислительную модель рассуждения с наилучшим объяснением множества данных в контексте ожидаемых причинных связей в предметной области.
Байесовские сети доверия - это направленный ациклический граф, обладающий следующими свойствами:
- каждая вершина представляет собой событие, описываемое случайной величиной, которая может иметь несколько состояний;
- все вершины, связанные с родителъскими, определяются таблицей условных вероятностей (ТУВ) или функцией условных вероятностей (ФУВ);
- для вершины без «родителей» вероятности состояний являются безусловными (маргинальными).
Другими словами, в байесовских сетях доверия вершины представляют собой случайные переменные, а дуга — вероятностные зависимости, которые определяются через таблицы условных вероятностей. Таблица условных вероятностей каждой вершины содержит вероятности состояний этой вершины при условии состояний её «родителей».
Слои Кохоненна
В своей простейшей форме слой Кохонена функционирует в духе «победитель забирает все», т. е. для данного входного вектора один и только один нейрон Кохонена выдает на выходе логическую единицу, все остальные выдают ноль. Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них.
Ассоциированное с каждым нейроном Кохонена множество весов соединяет его с каждым входом. Например, на рис. 4.1 нейрон Кохонена К 1 имеет веса w 11, w 21, …, w m1, составляющие весовой вектор W 1. Они соединяются-через входной слой с входными сигналами х 1, x 2, …, x m, составляющими входной вектор X. Подобно нейронам большинства сетей выход NET каждого нейрона Кохонена является просто суммой взвешенных входов. Это может быть выражено следующим образом:
NETj = w 1j x 1 + w 2j x 2 + … + w mj x m (4.1)
где NETj – это выход NET нейрона Кохонена j,
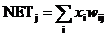 (4.2)
(4.2)
или в векторной записи
N = XW, (4.3)
где N – вектор выходов NET слоя Кохонена.
Нейрон Кохонена с максимальным значением NET является «победителем». Его выход равен единице, у остальных он равен нулю.
Слой Гроссберга
Слой Гроссберга функционирует в сходной манере. Его выход NET является взвешенной суммой выходов k 1, k 2,..., k n слоя Кохонена, образующих вектор К. Вектор соединяющих весов, обозначенный через V, состоит из весов v 11, v 21,..., v np. Тогда выход NET каждого нейрона Гроссберга есть
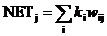 , (4.4)
, (4.4)
где NETj – выход j -го нейрона Гроссберга, или в векторной форме
Y = KV, (4.5)
где Y – выходной вектор слоя Гроссберга, К – выходной вектор слоя Кохонена, V – матрица весов слоя Гроссберга.
Если слой Кохонена функционирует таким образом, что лишь у одного нейрона величина NET равна единице, а у остальных равна нулю, то лишь один элемент вектора К отличен от нуля, и вычисления очень просты. Фактически каждый нейрон слоя Гроссберга лишь выдает величину веса, который связывает этот нейрон с единственным ненулевым нейроном Кохонена.
Сети Хопфилда.
На рис. 6.1 показана сеть с обратными связями, состоящая из двух слоев. Способ представления несколько отличается от использованного в работе Хопфилда и других, но эквивалентен им с функциональной точки зрения, а также хорошо связан с сетями, рассмотренными в предыдущих главах. Нулевой слой, как и на предыдущих рисунках, не выполняет вычислительной функции, а лишь распределяет выходы сети обратно на входы. Каждый нейрон первого слоя вычисляет взвешенную сумму своих входов, давая сигнал NET, который затем с помощью нелинейной функции F преобразуется в сигнал OUT. Эти операции сходны с нейронами других сетей (см. гл. 2).
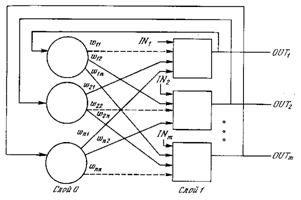
Однослойная сеть с обратными связями. Пунктирные линии обозначают нулевые веса
Состояние сети – это просто множество текущих значений сигналов OUT от всех нейронов. В первоначальной сети Хопфилда состояние каждого нейрона менялось в дискретные случайные моменты времени, в последующей работе состояния нейронов могли меняться одновременно. Так как выходом бинарного нейрона может быть только ноль или единица (промежуточных уровней нет), то текущее состояние сети является двоичным числом, каждый бит которого является сигналом OUT некоторого нейрона.
Когда подается новый входной вектор, сеть переходит из вершины в вершину, пока не стабилизируется. Устойчивая вершина определяется сетевыми весами, текущими входами и величиной порога. Если входной вектор частично неправилен или неполон, то сеть стабилизируется в вершине, ближайшей к желаемой.
Устойчивость. Как и в других сетях, веса между слоями в этой сети могут рассматриваться в виде матрицы W. В работе [2] показано, что сеть с обратными связями является устойчивой, если ее матрица симметрична и имеет нули на главной диагонали, т. е. если wij = wji и wii = 0 для всех i.
Любое изменение состояния нейрона либо уменьшит энергию, либо оставит ее без изменения. Благодаря такому непрерывному стремлению к уменьшению энергия в конце концов должна достигнуть минимума и прекратить изменение. По определению такая сеть является устойчивой.
Симметрия сети является достаточным, но не необходимым условием для устойчивости системы. Имеется много устойчивых систем (например, все сети прямого действия!), которые ему не удовлетворяют. Можно продемонстрировать примеры, в которых незначительное отклонение от симметрии может приводить к непрерывным осцилляциям. Однако приближенной симметрии обычно достаточно для устойчивости систем.
Описание APT
Сеть APT представляет собой векторный классификатор. Входной вектор классифицируется в зависимости от того, на какой из множества ранее запомненных образов он похож. Свое классификационное решение сеть APT выражает в форме возбуждения одного из нейронов распознающего слоя. Если входной вектор не соответствует ни одному из запомненных образов, создается новая категория посредством запоминания образа, идентичного новому входному вектору. Если определено, что входной вектор похож на один из ранее запомненных векторов с точки зрения определенного критерия сходства, запомненный вектор будет изменяться (обучаться) под воздействием нового входного вектора таким образом, чтобы стать более похожим на этот входной вектор.
Запомненный образ не будет изменяться, если текущий входной вектор не окажется достаточно похожим на него. Таким образом решается дилемма стабильности-пластичности. Новый образ может создавать дополнительные классификационные категории, однако новый входной образ не может заставить измениться существующую память.
Реализация нейронных сетей в виде оптических систем позволяет решить эту проблему. Взаимное соединение нейронов с помощью световых лучей не требует изоляции между сигнальными путями, световые потоки могут проходить один через другой без взаимного влияния. Более того, сигнальные пути могут быть расположены в трех измерениях. (Интегральные цепи являются существенно планарными с некоторой рельефностью, обусловленной множеством слоев.) Плотность путей передачи ограничена только размерами источников света, их дивергенцией и размерами детектора. Потенциально эти размеры могут иметь величину в несколько микрон. Наконец, все сигнальные пути могут работать одновременно, тем самым обеспечивая огромный темп передачи данных. В результате система способна обеспечить полный набор связей, работающих со скоростью света.
Оптические нейронные сети могут также обеспечить важные преимущества при проведении вычислений. Величина синаптических связей может запоминаться в голограммах с высокой степенью плотности; некоторые оценки дают теоретический предел в 1012 бит на кубический сантиметр. Хотя такие значения на практике не достигнуты, существующий уровень плотности памяти очень высок. Кроме того, веса могут модифицироваться в процессе работы сети, образуя полностью адаптивную систему.
Структура
Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, соответствующие последующим слоям, до тех пор, пока не достигнет выходного слоя, в котором идентифицируется распознаваемый образ.
Структура неокогнитрона трудна для представления в виде диаграммы, но концептуально проста. Чтобы подчеркнуть его многоуровневость (с целью упрощения графического представления), используется анализ верхнего уровня. Неокогнитрон показан состоящим из слоев, слои состоят из набора плоскостей и плоскости состоят из узлов.
Алгоритмы обучения
Большинство современных алгоритмов обучения выросло из концепций Хэбба [2]. Им предложена модель обучения без учителя, в которой синаптическая сила (вес) возрастает, если активированы оба нейрона, источник и приемник. Таким образом, часто используемые пути в сети усиливаются, и феномен привычки и обучения через повторение получает объяснение.
В искусственной нейронной сети, использующей обучение по Хэббу, наращивание весов определяется произведением уровней возбуждения передающего и принимающего нейронов. Это можно записать как
w ij(n +1) = w (n) + αOUTi OUTj,
где w ij(n) – значение веса от нейрона i к нейрону j до подстройки, w ij(n +1) – значение веса от нейрона i к нейрону j после подстройки, α – коэффициент скорости обучения, OUTi – выход нейрона i и вход нейрона j, OUTj – выход нейрона j.
Сети, использующие обучение по Хэббу, конструктивно развивались, однако за последние 20 лет были развиты более эффективные алгоритмы обучения. В частности, в работах [4 – 6] и многих других были развиты алгоритмы обучения с учителем, приводящие к сетям с более широким диапазоном характеристик обучающих входных образов и большими скоростями обучения, чем использующие простое обучение по Хэббу.
В настоящее время используется огромное разнообразие обучающих алгоритмов. Потребовалась бы значительно большая по объему книга, чем эта, для рассмотрения этого предмета полностью. Чтобы рассмотреть этот предмет систематически, если и не исчерпывающе, в каждой из последующих глав подробно описаны алгоритмы обучения для рассматриваемой в главе парадигмы. В дополнение в приложении Б представлен общий обзор, в определенной мере более обширный, хотя и не очень глубокий. В нем дан исторический контекст алгоритмов обучения, их общая таксономия, ряд преимуществ и ограничений. В силу необходимости это приведет к повторению части материала, оправданием ему служит расширение взгляда на предмет.
Цель обучения
Сеть обучается, чтобы для некоторого множества входов давать желаемое (или, по крайней мере, сообразное с ним) множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.
Обучение с учителем
Различают алгоритмы обучения с учителем и без учителя. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.
Обучение без учителя
Несмотря на многочисленные прикладные достижения, обучение с учителем критиковалось за свою биологическую неправдоподобность. Трудно вообразить обучающий механизм в мозге, который бы сравнивал желаемые и действительные значения выходов, выполняя коррекцию с помощью обратной связи. Если допустить подобный механизм в мозге, то откуда тогда возникают желаемые выходы? Обучение без учителя является намного более правдоподобной моделью обучения в биологической системе. Развитая Кохоненом [3] и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.
Метод пчелиной колонии
Для описания поведения пчёл в природе используются три основных понятия: источник нектара (цветок), занятые фуражиры, незанятые фуражиры.
Источник нектара характеризуется значимостью, определяемой различными факторами, такими как: удалённость от улья, концентрация нектара, удобство добычи нектара.
Занятые фуражиры закреплены за отдельным источником, на котором они добывают нектар, то есть они “заняты” им. Занятые фуражиры владеют такой информацией о данном источнике нектара, как: расстояние и направление от улья, полезность источника.
Незанятые фуражиры продолжают искать источники нектара для их использования. Существует два типа незанятых фуражиров: разведчики, которые ищут новые источники нектара, и наблюдатели, которые ждут в улье и могут выполнять другие действия в улье.
Среднее количество разведчиков в рое составляет 5-10%.
Несмотря на коллективный характер поведения общественных насекомых и на разные схемы этого поведения, отдельное насекомое также способно выполнять различные сложные действия, примером чего могут служить сбор и обработка нектара пчёлами, выполнение которых хорошо организовано.
Одной из часто возникающих задач в процессе моделирования сложных объектов и систем является нахождение глобального оптимума многомерной функции. Для решения это задачи применяется ряд методов (например, метод Коши, Ньютона, Левенберга-Марквардта и т.п.), которые, однако, требуют непрерывности, дифференцируемости и унимодаль ности целевых функций. Поэтому предлагается применять метод пчелиной колонии для решения задачи оптимизации многомерной функции.
Работу алгоритма можно представить в виде следующих шагов:
1. Задаются начальные параметры работы метода. В случае использования локальной оптимизации задаётся один из традиционных методов локальной оптимизации, который будет использоваться, и задаётся класс агентов, для решения которых будет применяться локальная оптимизация - агент с лучшим решением или агенты, выполнившие моделирование виляющего танца.
2. Создаются начальные агенты-разведчики.
a) Для каждого начального агента-разведчика создаётся случайное решение:
b) Для полученных случайных решений рассчитывается полезность данного источника нектара как значение оптимизируемой функции.
3. Выбираются рабочие агенты, т.е. такие агенты, на базе которых будут создаваться новые агенты с помощью процедуры скрещивания.
a) Определяется агент c наибольшей полезностью.
b) Процедура имитации отжига. 
4. Скрещивание. Поскольку реальные пчёлы-разведчики при выборе источника нектара пользуются также генетическим материалом (в биологии ещё не изучено, каким именно образом разведчики выбирают одни цветки и пропускают другие, то есть предполагается, что разведчики основываются на генетическом опыте), то с помощью процедуры скрещивания моделируется именно этот момент поведения пчёл. Для скрещивания используются ранее отобранные с помощью процедуры имитации отжига рабочие агенты workBee и лучший агент за все итерации best. Новые агенты создаются в два этапа. на базе решений рабочих агентов и на базе решения лучшего агента.
a) Создание новых агентов на базе рабочих агентов
b) Создание новых агентов на базе лучшего агента
c) Для всех новых агентов производится корректировка полученных решений.
d) Рассчитывается полезность полученных решений:
e) Выбирается новый лучший агент.
5. Моделирование выполнения виляющего танца. К возможному выполнению танца допускаются рабочие агенты workBee, агенты, созданные путём скрещивания, newWorkBee, лучший агент за все итерации best. Моделирование выполнения виляющего танца происходит в несколько этапов. В результате данного моделирования выбираются те агенты, которые за счёт выполнения танца выполнят вербовку других агентов для исследования найденного ими решения.
a) Выполняется нормирование полезностей агентов, допущенных к возможности выполнения танца. При этом нормирование учитывает направление оптимизации optOrient.
b) Добавление шумов к полученным нормированным полезностям и их корректировка.
c) Определение преимущества танца каждого агента.
d) Выбор тех агентов, которые за счёт выполнения танца выполняют вербовку других агентов для исследования найденного ими решения.
6. Если требуется проводить локальную оптимизацию для найденных лучших решений, тогда выполняется локальная оптимизация с помощью указанного метода локальной оптимизации (например, метод Нелдера-Мида, Хука-Дживса, Пауэлла и т.п.). В зависимости от установленных параметров локальная оптимизация выполняется либо для решений тех агентов, которые произвели вербовку, либо только для решения лучшего агента.
7. Выбирается агент с лучшим решением best.
8. Перезапуск агентов. Создаются агенты, которые будут рассматриваться как агенты-разведчики для следующей итерации.
К новым агентам-разведчикам будут относиться.
· агенты, выполнившие посредством танца вербовку, лучший агент;
· агенты, которые стали занятыми фуражирами вследствие вербовки. Поскольку такие агенты должны выполнять улучшенное изучение уже существующего источника с нектаром, то при создании решений для данных агентов должны учитываться решения завербовавших агентов. В связи с этим для завербованных агентов решение создаётся следующим образом:
· агенты, решение которых создаётся случайным образом:
Также для всех созданных агентов рассчитывается полезность выбранного решения.
9. Обновление динамических параметров метода:
10. Проверка на останов.
11. Если проверка на останов дала успешный результат, то выполняется переход к шагу 11, в противном случае - к шагу 3.
12. Конец.
Муравьиный алгоритм
Муравья нельзя назвать сообразительным. Отдельный муравей не в состоянии принять даже простейшего решения. Дело в том, что он устроен крайне примитивно: все его действия сводятся к элементарным реакциям на окружающую обстановку и своих собратьев. Муравей не способен анализировать, делать выводы и искать решения. Эти факты, однако, никак не согласуются с успешностью муравьев как вида. Они существуют на планете более 100 млн лет, строят огромные жилища, обеспечивают их всем необходимым и даже ведут настоящие войны.
Добиться таких успехов муравьи способны благодаря своей социальности. Они живут только в коллективах — колониях. Все муравьи колонии формируют так называемый роевой интеллект. Особи, составляющие колонию, не должны быть умными: они должны лишь взаимодействовать по определенным - крайне простым — правилам, и тогда колония целиком будет эффективна.
В колонии нет доминирующих особей, нет начальников и подчиненных, нет лидеров, которые раздают указания и координируют действия. Колония является полностью самоорганизующейся. Каждый из муравьев обладает информацией только о локальной обстановке, ни один из них не имеет представления обо всей ситуации в целом - только о том, что узнал сам или от своих сородичей, явно или неявно. На неявных взаимодействиях Муравьёв, называемых стигмергией, основаны механизмы поиска кратчайшего пути от муравейника до источника пищи.
Каждый раз, проходя от муравейника до источника пищи и обратно, муравьи оставляют за собой дорожку феромонов. Другие муравьи, почувствовав такие следы на земле, будут инстинктивно устремляться к источнику пищи. Поскольку эти муравьи тоже оставляют за собой дорожки феромонов, то чем больше муравьев проходит по определённому пути, тем более привлекательным он становится для их сородичей. При этом, чем короче путь до источника пищи, тем меньше времени требуется муравьям на него, а следовательно, тем быстрее оставленные на нем следы становятся заметными.
Имитируя поведение колонии Муравьёв в природе, муравьиные алгоритмы используют многоагентные системы, агенты которых функционируют по крайне простым правилам.
Классический муравьиный алгоритм. Как уже отмечалось, муравьиный алгоритм моделирует многоагентную систему. Её агентов в дальнейшем будем называть муравьями. Как и настоящие муравьи, они устроены довольно просто: для выполнения своих обязанностей они требуют небольшое количество памяти, а на каждом шаге работы выполняют несложные вычисления. Каждый муравей хранит в памяти список пройденных им узлов. Этот список называют списком запретов, или просто памятью муравья. Выбирая узел для следующего шага, муравей «помнит» об уже пройденных узлах и не рассматривает их в качест- ве возможных для перехода. На каждом шаге список запретов пополняется новым узлом, а перед новой итерацией алгоритма - т. е. перед тем, как мура. вей вновь проходит путь - он опустошается.
Кроме списка запретов при выборе узла для перехода муравей руководствуется «привлекательностью» рёбер, которые он может пройти. Она зависит, во-первых, от расстояния между узлами (т. е. от веса ребра), а во-вторых, от следов феромонов, оставленных на ребре прошедшими по нему ранее муравьями. Естественно, что в отличие от весов рёбер, которые являются константными, следы феромонов обновляются на каждой итерации алгоритма: как и в природе, со временем следы испаряются, а проходящие муравьи, напротив, усиливают их.
Жадные алгоритмы
Жадный алгоритм на каждом шаге делает локально оптимальный выбор в расчете на то, что итоговое решение также будет оптимальным. Это не всегда оправдано, но для многих задач жадные алгоритмы действительно дают оптимум.
Принцип жадного выбора
Говорят, что к оптимизационной задаче применим принцип жадного выбора (greedy choice property), если последовательность локально оптимальных (жадных) выборов дает глобально оптимальное решение. Различие между жадными алгоритмами и динамическим программированием можно пояснить так: на каждом шаге жадный алгоритм берет “самый жирный кусок”, а потом уже пытается сделать наилучший выбор среди оставшихся вариантов, каковы бы они ни были. Алгоритм динамического программирования принимает решение, просчитав заранее последствие всех вариантов.
Оптимальность для подзадач
Решаемые с помощью жадных алгоритмов задачи обладают свойством оптимальности для подзадач: оптимальное решение всей задачи содержит оптимальное решение подзадач.
И жадные алгоритмы, и динамическое программирование основываются на свойстве оптимальности для подзадач, поэтому может возникнуть желание применить жадный алгоритм вместо динамического, и наоборот. В одном случае это может не дать оптимального решения, во втором может привести к менее эффективному решению.
Алгоритм имитации отжига
В металлургии отжигом называется термическая обработка металла, заключающаяся в его нагреве до определенной температуры, выдержке и последующем - обычно медленном - охлаждении. Нагрев металла приводит к увеличению энергии его ионов и, соответственно, скорости диффузии. При этом ионы, не занимающие правильное место в кристаллической решетке, стремятся занять его. Естественно, что это ведет к уменьшению внутренних напряжений в металле - а значит, к повышению прочности, улучшению структуры и повышению однородности металла.
Алгоритм имитации отжига требует для работы единственного начального решения. На каждом шаге к текущему решению применяется оператор мутации и оно модифицируется случайным образом. Вычисляется энергия полученного состояния, и, если она окажется меньше энергии предыдущего, происходит безусловный переход к новому состоянию. Если энергия нового решения больше, чем энергия предыдущего, переход осуществляется с вероятностью, определяемой коэффициентом Больцмана.
Кроме того, в процессе работы алгоритма снижается значение температуры, что имитирует процесс медленного остывания металла при отжиге. При этом, поскольку температура определяет коэффициент Больцмана, постепенно снижается вероятность перехода системы к новому состоянию. Критерием останова алгоритма является достижение температурой минимального значения - нуля градусов.
Характер изменения температуры оказывает огромное влияние на тщательность исследования пространства поиска и скорость сходимости алгоритма. Наиболее очевидным вариантом является её линейное уменьшение, когда на каждом шаге алгоритма значение температуры уменьшается на некоторую константу, пока не достигнет нуля. Возможны, однако, и более сложные (и, вместе с тем, более эффективные) способы управления температурой. Можно снижать температуру от значения  до
до  каждые несколько итераций. Значение
каждые несколько итераций. Значение  , очевидно, должно лежать в пределах (0; 1). Также можно заранее выбрать число итераций
, очевидно, должно лежать в пределах (0; 1). Также можно заранее выбрать число итераций  и уменьшать значение температуры через каждые несколько итераций до значения
и уменьшать значение температуры через каждые несколько итераций до значения  , где константу
, где константу  обычно выбирают равной 1, 2 или 4. Чем больше ее значение, тем медленнее будет снижаться температура.
обычно выбирают равной 1, 2 или 4. Чем больше ее значение, тем медленнее будет снижаться температура.
Меметический алгоритм
Мем - единица культурного обмена, т. е. аналог гена в культуре. Мемом можно назвать жест, слово или идею; любая единица культурной информации, которая может быть передана от человека к человеку путём имитации или обучения — это мем.
Мемы ведут себя так же, как и гены. Мемы передаются между поколениями, мутируют и проходят отбор. Как и гены, мемы стремятся к саморепликации. Неудачные мемы постепенно исчезают, удачные надолго закрепляются в хозяевах, разносторонне влияя на их поведение.
В общих чертах меметический алгоритм состоит из следующих этапов:
Шаг 1. Создание начальной популяции. Особи в популяции могут быть сгенерированы случайным образом либо при помощи специальной процедуры инициализации.
Шаг 2. Локальный поиск. Каждая из особей в популяции осуществляв поиск локального оптимума в своей окрестности. Для осуществления локального поиска Москато использовал алгоритм имитации отжига. В более поздних работах предлагались менее сложные в вычислительном отношении алгоритмы, такие, как алгоритм подъёма. Оптимальным же является применение детерминированных алгоритмов, использующих информацию о структуре области поиска.
Шаг 3. Взаимодействие особей. Особи могут взаимодействовать двуМя способами: путём кооперации или соревнования. Кооперация. Для обмена информацией между особями может служить процедура, аналогичная применению оператора двухточечного скрещивания в генетических алгоритмах. Технически, при этом выбирается некоторый диапазон в пределах длины решения, и





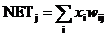 (4.2)
(4.2)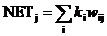 , (4.4)
, (4.4)

 до
до  каждые несколько итераций. Значение
каждые несколько итераций. Значение  , очевидно, должно лежать в пределах (0; 1). Также можно заранее выбрать число итераций
, очевидно, должно лежать в пределах (0; 1). Также можно заранее выбрать число итераций  и уменьшать значение температуры через каждые несколько итераций до значения
и уменьшать значение температуры через каждые несколько итераций до значения  , где константу
, где константу  обычно выбирают равной 1, 2 или 4. Чем больше ее значение, тем медленнее будет снижаться температура.
обычно выбирают равной 1, 2 или 4. Чем больше ее значение, тем медленнее будет снижаться температура.


