

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Точки локального экстремума. Пусть c - точка из области определения функции.
Точку x0 называют точкой локального максимума функции f(x), если существует такая окрестность 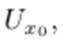 что
что 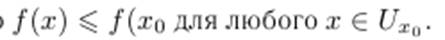 .
.
Точку x0 называют точкой локального минимума функции f(x), если существует такая окрестность, что
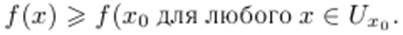
Точки локального максимума и локального минимума функции называют точками локального экстремума.
Стационарные точки функции. Пусть функция дифференцируема в точке c. Точка c называется стационарной точкой функции f(x), если 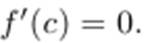 .
.
Теорема Ферма. Пусть функция f(x) определена на (a,b) и x0 ∈ (a,b) - точка локального экстремума. Если функция дифференцируема в точке x0, то x0 является стационарной точкой функции.
Теорема Ролля. Пусть функция f(x) непрерывна на [a,b] и дифференцируема на (a,b). Если f(a) = f(b), то на интервале (a,b) существует по крайней мере одна стационарная точка.
Конечные приращения. Пусть функция определена по меньшей мере на отрезке [a,b].
Теорема Лагранжа. Если функция f(x) непрерывна на [a,b] и дифференцируема на (a,b), то на (a,b), существует такая точка c, что 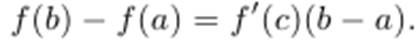
Если функция f(x) непрерывна на отрезке с концами a и b и дифференцируема внутри его, то существует такое число θ ∈ (0, 1), что 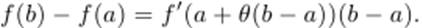 Эту формулу называют формулой конечных приращений. Ее записывают также в виде
Эту формулу называют формулой конечных приращений. Ее записывают также в виде 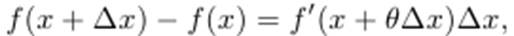
Теорема Коши. Если функции f(x) и g(x) непрерывны на [a,b], дифференцируемы на (a,b) и 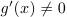 на (a,b), то на (a,b), существует такая точка c, что
на (a,b), то на (a,b), существует такая точка c, что 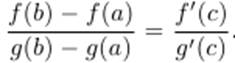
Правила Лопиталя
Пусть X - некоторый промежуток и a предельная точка множества X. Допускаем, что a может быть и +∞ или −∞. Рассмотрим функцию f(x), определенную на множестве 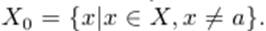 Если a - граничная точка промежутка X, то при рассмотрении
Если a - граничная точка промежутка X, то при рассмотрении 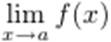 рассматриваем соответствующий односторонний предел.
рассматриваем соответствующий односторонний предел.
|
|
Первое правило Лопиталя. Пусть
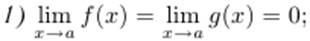
2) функции f(x) и g(x) дифференцируемы на X0;
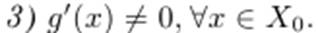
Если существует предел (конечный или бесконечный) 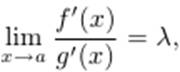 то и
то и 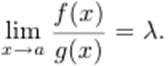
Второе правило Лопиталя. Пусть
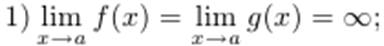
2) функции f(x) и g(x) дифференцируемы на X0;
3) 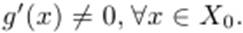
Если существует предел (конечный или бесконечный) 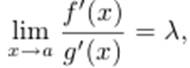 то и
то и 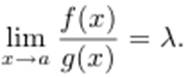
Производные высших порядков. Дифференциал. Дифференциалы высших порядков.
Последовательное дифференцирование
Для функции y = f(x) производной второго порядка называют производную функции 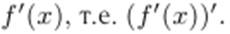 Обозначают
Обозначают 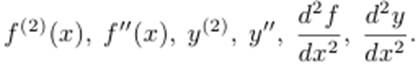 Таким образом,
Таким образом, 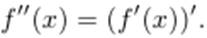
Для функции y = f(x) производной порядка n называют производную производной порядка n−1. Таким образом 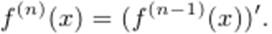
Теорема 2.36 (Формула Лейбница). Если функции u = u(x), v = v(x) имеют производные порядка n, то
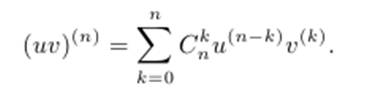
Дифференцирование функций, задаваемых параметрически
Теорема 2.37. Пусть формулы x = ϕ(t), y = ψ(t), t ∈ T задают параметрически функцию y = y(x). Если
функции ϕ(t) и ψ(t) дифференцируемы и ϕ’(t) =/ 0, то функция y = y(x) дифференцируема и ее производная y’(x) задается параметрически формулами

Дифференциалы
Дифференцируемость функции означает, что ее приращение представимо в виде ∆y = A · ∆x + o(∆x).
Главную часть приращения функции 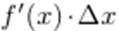 называют дифференциалом и обозначают
называют дифференциалом и обозначают 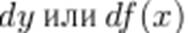 Таким образом,
Таким образом, 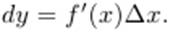
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!