Тема 8. Предел и непрерывность функций

 

Не повторяя данных в учебнике определений и доказательств, рассмотрим ряд конкретных примеров, в которых отражена сущность теории пределов.

 

Пример 1.

 

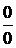
Подстановка на место x его предельного значения, т.е. числа 2, приводит к неопределенности вида 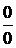. Преобразуем дробь до перехода к пределу, разложив числитель и знаменатель на множители

 

теперь имеем _.

 

Пример 2.

 

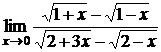
Подстановка предельного значения x (т.е. числа 0) приводит к неопределенности вида 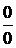_. Преобразуем дробь под знаком предела до того как .

_{= .}

 

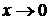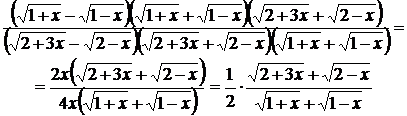
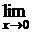
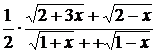Пример 3.

Найти .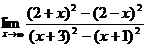

Здесь выражение под знаком пределов представляет собой отношение двух многочленов аргумента n. И числитель и знаменатель дроби стремятся к бесконечности. В этом случае говорят, что имеется «неопределенность типа ».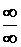

Для отыскания предела следует раскрыть скобки и разделить числитель и знаменатель на высшую степень.

Получаем

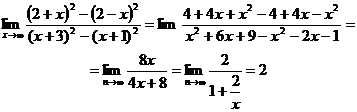
Так как 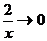при .

Пример 4.

Найти _.

 

Как и в примере 3 целесообразно числитель и знаменатель дроби разделить на старшую степень, которую легко увидеть, если под каждым корнем оставить лишь старшую степень n (остальные слагаемые играют малую роль при ).

В данном примере получаем .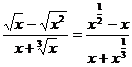

Значит старшая степень -x. Разделив числитель и знаменатель на x, будем иметь 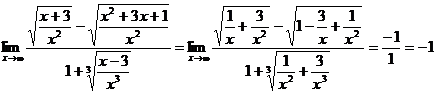, так как 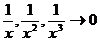при x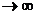

 

Пример 5.

Найти .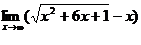

Здесь мы имеем «неопределенность типа ()».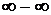

Умножив и разделив эту разность на сопряженное выражение 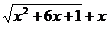, получим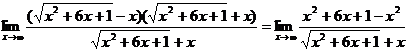

.

Такой предел рассматривался в предыдущем примере. Разделив числитель и знаменатель на x, будем иметь .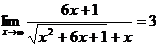

Пример 6.

Вычислить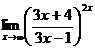

Здесь основание степени 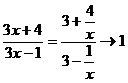при x 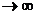,а показатель 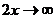; таким образом имеем «неопределенность типа 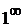». В этом случае следует воспользоваться вторым замечательным пределом:

.

 

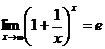Преобразовав выражение, получаем

,

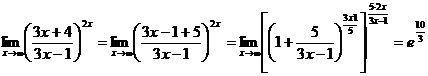так как выражение в квадратных скобках стремится к е, а 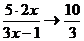при .

Пусть, например, требуется вычислить .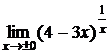

Рассмотрим случай 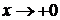, тогда показатель стремится к , основание к 4, значит искомый предел равен . Если 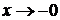, то показатель 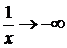,основание стремится к 4 и искомый предел равен 0. Итак

.

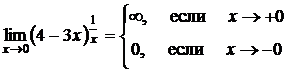Пример 7.

Найти .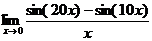

Для решения применим предел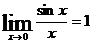

Здесь при 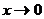и числитель и знаменатель стремятся к нулю, получаем «неопределенность типа 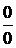». Используя формулу тригонометрии

имеем

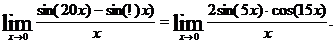
Заметим, что cos(15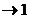x) при x , поэтому

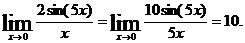
Пример 8.

Найти _.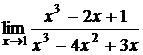

 

Известно (следствие теоремы Безу), что если многочлен обращается в нуль при _, то он делится без остатка на 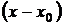, поскольку и числитель и знаменатель рассматриваемой дроби обращается в нуль при х=1 «неопределенность типа 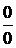», то как и в предыдущей задаче, можно сократить дробь на х-1. Разделив числитель и знаменатель на x-1

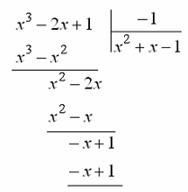
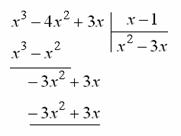
получаем

.

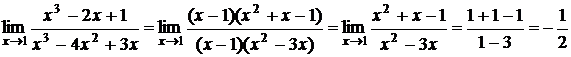Пример 9.

Найти точки разрыва функции 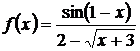. Изобразить график в окрестности точки разрыва.

Знаменатель 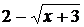, при х=1 обращается в нуль и значит f(x) при x=1 не существует, следовательно, x=1 - точка разрыва функции. Для определения типа разрыва надо найти пределы функции слева и справа при х=1.

При тех же рассуждениях получим .

 

Итак, пределы функции слева и справа при равны, но в точке x=1 функция не определена, значит, точка устранимого разрыва. График функции в окрестности точки разрыва выглядит следующим образом:

 

Такой разрыв называют устранимым разрывом, так как доопределив функцию f(x) надлежащим образом (положив при x=1 f(x) =4) получим непрерывную функцию:

.

 

 

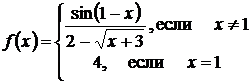ТЕМА 9. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ

При освоении техники дифференцирования необходимо заучить таблицу производных основных элементарных функций и научиться пользоваться основными правилами дифференцирования. При этом особое внимание следует уделить дифференцированию сложных функций.

Пример.1

.

Данную функцию можно представить в виде цепочки двух простых функций: ; .Согласно правилу дифференцирования сложной функции имеем: .

Но , а потому .

 

Пример 2.

.

Очевидно, что и тогда ,так как , то .

В двух рассмотренных примерах каждая из сложных функций содержала лишь один промежуточный аргумент u и поэтому разлагалась на цепочку из двух простых функций. В более сложных случаях промежуточных аргументов может оказаться больше одного.

 

ИССЛЕДОВАНИЕ ФУНКЦИЙ

 

В дополнение к примерам, разобранным в тексте учебника, рассмотрим еще следующий пример.

Пример. Исследовать функцию и построить ее график.

1. Область определения данной функции - вся числовая ось, кроме точки

2. Функция не является ни четной, ни нечетной. Действительно, f(-x)= и -f(x).

 

3. Прямая есть вертикальная асимптота, так как точка есть точка разрыва второго рода.

4.Найдем угловой коэффициент наклонной асимптоты, предполагая, что такая существует: ; .

Находим свободный член b для уравнения асимптоты:

.

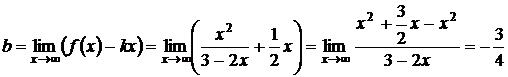Итак, уравнение асимптоты: .

 

5. Находим критические точки, т.е. точки, в которых первая производная обращается в нуль: .

Производная обращается в нуль, если , и .

Подвергая испытанию каждую из этих двух точек, можно узнать, меняется ли знак производной при прохождении аргумента через точки 0 и 3:

а) y¢<0 при x<0 (функция убывает), y¢>0 при x>0 ¢ (функция y возрастает), следовательно, в точке x=0 функция y достигает минимума, причем ;

б) при x<3 y¢>0 (возрастает); x>3 y¢<0 (убывает).

Таким образом, в точке x=3 функция достигает максимума, равного .

6. Для уточнения графика функции найдем точки перегиба и установим направление вогнутости (выпуклости) кривой в различных интервалах, для чего обращаемся ко второй производной). Положительный множитель 2, входящий в первую производную, может быть отброшен, поскольку он не влияет на знак второй производной. Имеем

Если , то y²>0 и кривая обращена вогнутостью вверх.

При знаменатель (3- 2х)³ <0 и .

 

Следовательно, справа от точки разрыва кривая обращена вогнутостью вниз. Точек перегиба нет, y² ни при каком значении из области определения не обращается в нуль. Принимая во внимание выводы всех предыдущих пунктов, строим график функции