

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Векторы  называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация  при не равных нулю одновременно
при не равных нулю одновременно  . Если же только при ai = 0 выполняется
. Если же только при ai = 0 выполняется  , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.
2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
6. Любые 4 вектора линейно зависимы.
13. Скалярное произведение векторов, его cв=ва. евклидово пространство.
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними. 


скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства:
1.  причем
причем 
2. 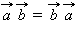 переместительный закон
переместительный закон
3.  распределительный закон
распределительный закон
4. 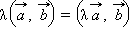 сочетательный закон
сочетательный закон
Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.
Прямая на плоскости. Ур-е прямой с угловым коэффициентом. Ур-е прямой, проход через данную точку, в заданном направлении. Ур-е прямой, проход через 2 данные точки.
0 ≤α≤π  -ур-ие прямой с угловым коэффиц. Подставим
-ур-ие прямой с угловым коэффиц. Подставим 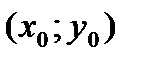 в (1);
в (1);  (3)-ур-ие пр., проход. ч/з задан(.) с зад. угловым коэффициентом
(3)-ур-ие пр., проход. ч/з задан(.) с зад. угловым коэффициентом
 ;
;
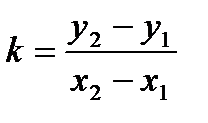 , подст. в ур (3):
, подст. в ур (3):  - ур-ие прямой ч/з 2 данные точки.
- ур-ие прямой ч/з 2 данные точки.
Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.
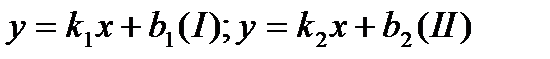


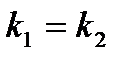 -условие паралл-ти прямых;
-условие паралл-ти прямых;

 -усл. перпендик-ти прямых
-усл. перпендик-ти прямых
Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как 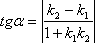 .
.
Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как 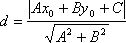
Уравнение прямой в отрезках. Общее уравнение прямой на плоскости.
Вектор n = (А; В) - нормальный вектор прямой.
В векторном виде: n*r + С = 0, где - радиус-вектор произвольной точки на прямой.
Частные случаи:
1) By + C = 0 - прямая параллельна оси Ox;
2) Ax + C = 0 - прямая параллельна оси Oy;
3) Ax + By = 0 - прямая проходит через начало координат;
4) y = 0 - ось Ox;
5) x = 0 - ось Oy.
 Уравнение прямой в отрезках
Уравнение прямой в отрезках 
где a, b - величины отрезков, отсекаемых прямой на осях координат.
общее уравнение прямой на плоскости Ах+Ву+С=0:
Ву=-Ах-С (А,В,С не равно 0)
У=(-А/В)*х-С/В
k= -А/В=tgα
Общее уравнение плоскости.
Ax+By+Сz-Ax0-By0-Сz0=0
-Ax0-By0-Сz0=D, где D=Ax+By+Сz
Ax+By+Сz+D=0
Частный случай:
Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)
Если A=0, то By+Сz+D=0
Если B=0, то Ax +Сz+D=0
Если C=0, то Ax+By+D=0
Если A=B=0, то Сz+D=0
Если A=C=0, то By+D=0
Если A=D=0, то By+Сz=0
Если B=D=0, то Ay+Сz=0
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!