

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Задача 18. Сколькими способами могут восемь человек стать в очередь к театральной кассе?
Решение задачи: Существует 8 мест, которые должны занять 8 человек. На первое место может стать любой из 8 человек, т.е. способов занять первое место – 8. После того, как один человек стал на первое место, осталось 7 мест и 7 человек, которые могут быть на них размещены, т.е. способов занять второе место – семь. Аналогично для третьего, четвертого и т.д. места. Используя принцип умножения, получаем произведение –  . Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8. Ответ: P8 = 8!
. Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8. Ответ: P8 = 8!
Задача 19. Позывные радиостанции должны начинаться с буквы W. 1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из трех букв, причем эти буквы могут повторяться? 2) Если позывные состоят из четырех букв, которые не повторяются?
Решение задачи:
В современном латинском алфавите 26 букв. На первом месте всегда должна стоять одна буква, следовательно, существует только один способ занять первое место.
1) На оставшиеся два места может претендовать любая из 26-ти букв, т.к. буквы в позывных могут повторяться. Используя принцип умножения, получаем произведение: 1  = 262.
= 262.
2) На второе место можно поставить любую из 25 букв, т.к. в позывных буквы не должны повторяться. На третье место – 24 буквы, на четвертое место – 23 буквы. Используя принцип умножения, получаем произведение: 1 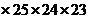 . Ответ: 1) 262; 2)
. Ответ: 1) 262; 2) 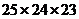 .
.
Задача 20. В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?
Решение задачи:
Действие, которое должно быть выполнено особым способом, необходимо выполнять первым. Итак, на место водителя можно посадить только одного из трех человек (умеющего водить машину), т.е. существуют 3 способа занять первое место. Второе место может занять любой из 6 человек, оставшихся после того, как место водителя будет занято. И т.д. Используя принцип умножения, получаем произведение: 3  = 3
= 3  6! = 3
6! = 3  P6. Ответ: 3
P6. Ответ: 3  P6 = 3
P6 = 3  6!.
6!.
|
|
Задача 21. Алфавит некоторого языка содержит 30 букв. Сколько существует шестибуквенных слов (цепочка букв от пробела до пробела), составленных из букв этого алфавита, если:
1) буквы в словах не повторяются?
2) буквы в словах могут повторяться?
Решение задачи:
Существует шесть мест, на которые нужно разместить 30 букв.
1. Буквы не должны повторяться. Используя принцип умножения, получаем произведение: 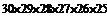 . Такое произведение достаточно сложно использовать в дальнейшем, и информация задачи представлена в ней в скрытой форме. В комбинаторике используют для таких произведений формулу размещений. Чтобы получить формулу размещений, умножим это произведение на единицу, которую представим следующим образом:
. Такое произведение достаточно сложно использовать в дальнейшем, и информация задачи представлена в ней в скрытой форме. В комбинаторике используют для таких произведений формулу размещений. Чтобы получить формулу размещений, умножим это произведение на единицу, которую представим следующим образом: 
 1 =
1 = 
 =
= 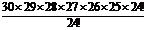 =
= 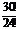 =
= 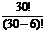 = А
= А 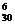 ‑ формула для размещений.
‑ формула для размещений.
2. Буквы повторяются. Используя принцип умножения, получаем: 30  30
30  30
30  30
30  30
30  30 = 306 = Ã
30 = 306 = Ã 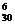 – формула для размещений с повторениями.
– формула для размещений с повторениями.
Ответ: 1) А 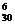 ; 2) Ã
; 2) Ã 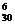 .
.
Задача 22. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?
Решение задачи:
Необходимо посчитать, сколько существует трехзначных, четырехзначных и пятизначных чисел, составленных из этих пяти цифр. Трехзначных чисел - 5  4
4  3 = А
3 = А 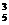 , четырехзначных – 5
, четырехзначных – 5  4
4  3
3  2 = А
2 = А  , пятизначных – 5
, пятизначных – 5  4
4  3
3  2
2  1 = А
1 = А  . Используем принцип сложения: А
. Используем принцип сложения: А 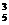 + А
+ А  + А
+ А  = 60 + 120 + 120 = 300. Ответ: 300.
= 60 + 120 + 120 = 300. Ответ: 300.
|
|
|

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!