Свойство 3 является следствием формулы бинома Ньютона:
 . (9.1)
. (9.1)
Поэтому сочетания еще иногда называют биномиальными коэффициентами.
Сумма биномиальных коэффициентов всех членов разложения равна 2 n. Сумма биномиальных коэффициентов членов разложения, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах, и равно 2 n– 1.
Пример 9.1. Найти разложение степени бинома (2 x –3)5.
Решение. Полагая a =2 x, b =–3, получим
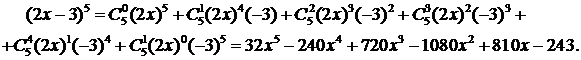
Пример 9.2. Пятый член разложения  не зависит от x. Найти n.
не зависит от x. Найти n.
Решение. Пятый член разложения T 5 имеет следующий вид:
 .
.
По условию T 5 не зависит от x; это означает, что показатель степени при x равен нулю, т.е. (n –4)/3–4=0. Из последнего уравнения находим n =16.
Пример 9.3. Вычислить сумму
 .
.
Решение. Согласно формуле бинома Ньютона, при любом x имеем равенство:
 .
.
Полагая здесь x =1, получим
 .
.
Итак, искомая сумма равна 35, т.е. 243.
Упражнения
9.1. Напишите разложение степени бинома
а)  ; б)
; б)  ; в)
; в)  .
.
Ответ: а)  ,
,
б)  ,
,
в) 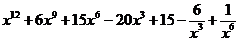 .
.
9.2. Найдите пятый член разложения 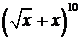 .
.
Ответ:  .
.
9.3. Найдите два средних члена разложения  .
.
Ответ:  и
и 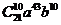 .
.
9.4. Найдите в биномиальном разложении  член, не содержащий x.
член, не содержащий x.
Ответ:  .
.
9.5. Найдите сумму  .
.
Ответ:  .
.
9.6. Сумма биномиальных коэффициентов разложения 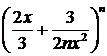 равна 64. Напишите член, не содержащий переменную x.
равна 64. Напишите член, не содержащий переменную x.
Ответ: n =6, 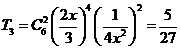 .
.
РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ
Пусть выбор k элементов из некоторого множества, состоящего из n элементов, производится с возвращением и с упорядочением их в последовательную цепочку. Различными исходами такого выбора будут всевозможные наборы (вообще говоря, с повторениями) отличающиеся либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями из n элементов по k элементов.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента: ab, ac, ba, bc, ca, cb, aa, bb, cc.
Таким образом, размещение с повторениями из n элементов по k элементов (при этом допускается, что m > n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т.е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Число размещений с повторениями  можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т.д. По принципу умножения находим
можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т.д. По принципу умножения находим
 . (10.1)
. (10.1)
Пример 10.1. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т.е. набор упорядоченный), причем возможны повторения (т.е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Пример 10.2. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?
Решение. Данная задача есть задача на отыскание числа размещений с повторениями
 .
.
Пример 10.3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно  .
.
Число всех букв, каждая из которых записывается двумя символами, равно  .
.
Число всех букв, каждая из которых записывается тремя символами, равно 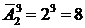 .
.
Число всех букв, каждая из которых записывается четырьмя символами, равно 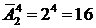 .
.
Число всех букв, каждая из которых записывается пятью символами, равно  .
.
Число всех указанных букв будет равно 62.
Упражнения
10.1. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?
Ответ:  .
.
10.2. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?
Ответ:  .
.
10.3. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
Ответ:  .
.
10.4. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?
Ответ:  .
.
10.5. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа  (повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a =1; 2) a¹2; 3) a =3, b =2; 4) a =3, b =4, c =5?
(повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a =1; 2) a¹2; 3) a =3, b =2; 4) a =3, b =4, c =5?
Ответ: 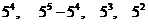 .
.
10.6. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2 k k -значных числа, то общее количество искомых чисел равно  . б) Для трёх цифр аналогично получаем
. б) Для трёх цифр аналогично получаем 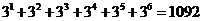 . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим
. в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим  чисел.
чисел.
10.7. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т.е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше:  способов выбора кур. Точно так же есть
способов выбора кур. Точно так же есть  способов выбора уток и
способов выбора уток и 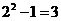 способов выбора гусей. Всего
способов выбора гусей. Всего  способов.
способов.
ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИ
При перестановке букв в слове «толпа» получается P 5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет  . Мы имеем здесь дело с перестановками с повторениями.
. Мы имеем здесь дело с перестановками с повторениями.
Общую задачу сформулируем следующим образом.
Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа,  . Сколько можно составить различных перестановок из этих элементов?
. Сколько можно составить различных перестановок из этих элементов?
Число перестановок c повторениями обозначают  . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n 1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n 2! перестановок элементов во второй группе и т.д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом
. Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n 1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n 2! перестановок элементов во второй группе и т.д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом 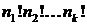 способами так, что она остаётся неизменной.
способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно
 , (11.1)
, (11.1)
где  .
.
Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:
 .
.
Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k 1=4 элементов первого типа (зеленых бус), k 2=5 элементов второго типа (синих бус) и k 3=6 элементов третьего типа (красных бус). По формуле (6) получаем
 .
.
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?
Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:
 .
.
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Камни можно переставлять P (5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем
 .
.
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?
Решение. а) Буквы данного слова можно переставлять P (3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим
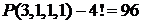 .
.
б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить  способами. Всего получаем
способами. Всего получаем  способа.
способа.
Упражнения
11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?
Ответ: 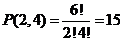 .
.
11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?
Ответ:  .
.
11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?
Ответ:  .
.
11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?
Ответ:  .
.
11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?
Ответ:  .
.
11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?
Ответ: 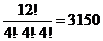 .
.
11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Ответ:  .
.
11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?
Ответ:  .
.
11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Ответ: Гласные можно переставлять P (2,1,1)=12 способами, Аналогично, P (2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать  способами. Всего
способами. Всего  способов.
способов.
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
Пусть имеются предметы n различных типов. Сколькими способами можно составить из них комбинацию из k элементов, если не принимать во внимание порядок элементов в комбинации, но при этом предметы одного и того же типа могут повторяться? Иными словами, различные комбинации должны отличаться количеством предметов хотя бы одного типа. Такие комбинации называются сочетаниями с повторениями, а их общее число будем обозначать  .
.
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть сочетаний с повторениями по два элемента: ab, ac, bc, aa, bb, cc.
Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что m > n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т.е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Следует отметить, что если, например, две комбинации по k элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.
Существует специальная формула для вычисления числа сочетаний с повторениями:
 (12.1)
(12.1)
Выведем эту формулу. Прежде всего надо занумеровать возможные типы элементов числами от 1 до n (иначе можно оказаться в положении мужа, который никак не мог вспомнить, что ему поручила купить жена: 5 пакетов молока и 2 банки пива или наоборот 2 пакета молока и 5 банок пива). Теперь можно каждую комбинацию зашифровать с помощью последовательности единиц и палочек: для каждого типа с 1-го до n -го по порядку написать столько единиц, сколько предметов этого типа входит в комбинацию, а различные типы отделять друг от друга палочками.
Например, в кондитерском магазине продаются пирожные 4 видов: корзиночки, наполеоны, песочные и эклеры. Если куплено 3 корзиночки (к), 1 наполеон (н), 2 песочных (п) и 1 эклер (э), то получим такую запись:

В этой записи палочки отделяют одну группу пирожных от другой. Если же куплено 2 корзиночки и 5 песочных, то получим запись  . Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации
. Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации  соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
В результате мы получим столько единиц, сколько предметов входит в комбинацию, т.е. k, а число палочек будет на 1 меньше, чем число типов предметов, т.е. n –1. Таким образом, мы получим перестановки с повторениями из k единиц и n –1 палочек. Различным комбинациям при этом соответствуют различные перестановки с повторениями, а каждой перестановке с повторениями соответствует своя комбинация.
Итак, число  сочетаний с повторениями из элементов n типов по k равно числу P (k, n –1) перестановок с повторениями из n –1 палочек и k единиц. А
сочетаний с повторениями из элементов n типов по k равно числу P (k, n –1) перестановок с повторениями из n –1 палочек и k единиц. А  . Поэтому
. Поэтому  .
.
Пример 12.1. В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?
Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,

Пример 12.2. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний с повторениями из 10 элементов по 10. Следовательно,
 ,
, 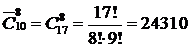 .
.
В случае, когда требуется купить 8 различных открыток, получим сочетания без повторений:
 .
.
Пример 12.3. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку  ,
,  ,
,  ,
,  ,
,  , то существует
, то существует  чисел, удовлетворяющих условию задачи.
чисел, удовлетворяющих условию задачи.
Упражнения
12.1. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?
Ответ:  .
.
12.2. В кондитерской имеется пять разных сортов пирожных. Сколькими способами можно выбрать набор из четырёх пирожных?
Ответ: 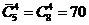 .
.
12.3. Сколько существует треугольников, длины сторон которых принимают одно из значений 4, 5, 6, 7?
Ответ:  .
.
12.4. Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10?
Ответ:  .
.



 . (9.1)
. (9.1)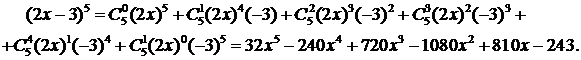
 не зависит от x. Найти n.
не зависит от x. Найти n. .
. .
. .
. .
. ; б)
; б)  ; в)
; в)  .
. ,
, ,
,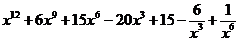 .
.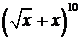 .
. .
. .
. и
и 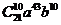 .
. член, не содержащий x.
член, не содержащий x. .
. .
. .
.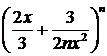 равна 64. Напишите член, не содержащий переменную x.
равна 64. Напишите член, не содержащий переменную x.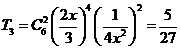 .
. можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т.д. По принципу умножения находим
можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т.д. По принципу умножения находим . (10.1)
. (10.1)
 .
. .
. .
.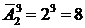 .
.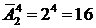 .
. .
. .
. .
. .
. .
. (повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a =1; 2) a¹2; 3) a =3, b =2; 4) a =3, b =4, c =5?
(повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a =1; 2) a¹2; 3) a =3, b =2; 4) a =3, b =4, c =5?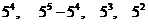 .
. . б) Для трёх цифр аналогично получаем
. б) Для трёх цифр аналогично получаем 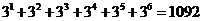 . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим
. в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим  чисел.
чисел. способов выбора кур. Точно так же есть
способов выбора кур. Точно так же есть  способов выбора уток и
способов выбора уток и 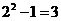 способов выбора гусей. Всего
способов выбора гусей. Всего  способов.
способов. . Мы имеем здесь дело с перестановками с повторениями.
. Мы имеем здесь дело с перестановками с повторениями. . Сколько можно составить различных перестановок из этих элементов?
. Сколько можно составить различных перестановок из этих элементов? . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n 1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n 2! перестановок элементов во второй группе и т.д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом
. Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n 1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n 2! перестановок элементов во второй группе и т.д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом 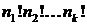 способами так, что она остаётся неизменной.
способами так, что она остаётся неизменной. , (11.1)
, (11.1) .
. .
. .
. .
. .
.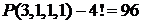 .
. способами. Всего получаем
способами. Всего получаем  способа.
способа.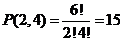 .
. .
. .
. .
. .
.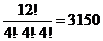 .
. .
. .
. способами. Всего
способами. Всего  способов.
способов. .
. (12.1)
(12.1)
 . Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации
. Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации  соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют). . Поэтому
. Поэтому  .
.
 ,
, 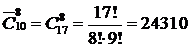 .
. .
. ,
,  ,
,  ,
,  ,
,  , то существует
, то существует  чисел, удовлетворяющих условию задачи.
чисел, удовлетворяющих условию задачи. .
.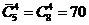 .
. .
. .
.


