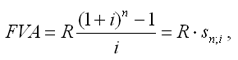Расчет процентов с использование процентных чисел

В банковской практике размещенный на длительное время капитал может в течение этого периода времени изменяться, т.е. увеличиваться или уменьшаться путем дополнительных взносов или отчислений. Таким образом, при обслуживании счетов банки сталкиваются с непрерывной сетью поступлений и расходованием средств и начислением процентов на постоянно меняющуюся сумму. В этой ситуации в банковской практике используется правило: общая начисленная за весь срок сумма процентов равна сумме процентов, начисленных на каждую из постоянных на некотором отрезке времени сумм.

Это касается и дебетовой, и кредитовой части счета. Разница лишь в том, что кредитовые проценты вычитаются.

В таких случаях для расчета процентов используется методика расчета с вычислением процентных чисел: каждый раз, когда сумма на счете изменяется, производится расчет " процентного числа " за период, в течение которого сумма на счете была неизменной. Процентное число вычисляется по формуле:

Процентное число =

(Сумма на счете • Длительность периода в днях)/100

= (PV • t) / 100

Для определения суммы процентов за весь срок их начисления все "процентные числа" складываются, и их сумма делится на постоянный делитель, который носит название " процентный ключ " или дивизор, определяемый отношением количества дней в году к годовой процентной ставке:

I = Σ Процентных чисел: Постоянный делитель,

где

Постоянный делитель = Продолжительность года в днях / Годовая ставка процентов = T / i

Проценты, вычисляемые с использованием дивизора, рассчитанного исходя из 365 дней в году, будут меньше, чем проценты по дивизору, где количество дней в году принято за 360, поэтому при обслуживании конкретного клиента всегда используется один из дивизоров.

Методика с использованием процентных чисел по своей сути является последовательным применением формулы простых процентов для каждого интервала постоянства суммы на счете:

I = I₁ + I₂ + I₃ = P₁ • t₁/T • i + P₂ • t₂/T • i + P₃ • t₃/T • i

Пример. При открытии сберегательного счета по ставке 28% годовых, 20 мая 1999 года была положена сумма в размере 1'000 рублей, а 5 июля на счет добавлена сумма в 500 руб., 10 сентября снята со счета сумма в 750 руб., а 20 ноября счет был закрыт. Используя процентные числа определить сумму начисленных процентов при ус-ловии, что банк использует "германскую практику".

Решение:

Срок хранения суммы в 1000 руб. составил 46 дней, тогда

Процентное число ₁ = (1000 • 46)/100 = 460;

срок хранения суммы в размере 1500 руб. составил 66 дней, откуда

Процентное число ₂ = (1500 • 66)/ 100 = 990;

срок хранения уменьшенной до 750 руб. суммы составил 70 дней:

Процентное число ₃ = (750 • 70)/100 = 525

Дивизор = 360/28 = 12,857

Следовательно, сумма начисленных процентов за период действия сберегательного счета составит:

I = (460 + 990 + 525)/12,857 = 153,61 руб.

Можно проверить правильность произведенных нами расчетов, исходя из сути процентов:

I = 1000 • 46/360 • 0,28 + 1500 • 66/360 • 0,28 + 750 • 70/360 • 0,28 = 153,61 руб.

Как видим, результат вычислений тот же самый.

 

Здесь годовая процентная ставка берется в виде процента, а не коэффициента.

 

В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов.

Применение схемы сложных процентов целесообразно в тех случаях, когда:

ü проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;

ü срок ссуды более года.

FV = PV • (1 + i) ⁿ = PV • k_н,

где FV – наращенная сумма долга;

PV – первоначальная сумма долга;

i – ставка процентов в периоде начисления;

n – количество периодов начисления;

k_н – коэффициент (множитель) наращения сложных процентов.

Эта формула называется формулой сложных процентов.

Период начисления по сложным процентам не всегда равен году, однако в условиях финансовой операции указывается не ставка за период, а годовая ставка с указанием периода начисления – номинальная ставка (j).

Номинальная ставка (nominal rate) – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год.

Эта ставка

ü во-первых, не отражает реальной эффективности сделки;

ü во-вторых, не может быть использована для сопоставлений.

Если начисление процентов будет производиться m раз в год, а срок долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит

N = n • m

 

Отсюда формулу сложных процентов можно записать в следующем виде:

 

FV = PV • (1 + j/m)^N = P • (1 + j/m)^mn

где j – номинальная годовая ставка процентов.

 

До сих пор мы рассматривали случаи финансовых операций, состоящих из отдельного разового платежа, например, получение и погашение долгосрочной ссуды. Вместе с тем, погашение такой ссуды возможно не только единовременным платежом, но множеством распределенных во времени выплат. В финансовой литературе ряд распределенных во времени выплат и поступлений называется потоком платежей.

Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т. п.

Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а временные интервалы между членами такого потока могут быть равными и неравными.

Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.

При рассмотрении финансовой ренты используются основные категории:

ü член ренты (R) – величина каждого отдельного платежа;

ü период ренты (t) – временной интервал между членами ренты;

ü срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода;

ü процентная ставка (i) – ставка, используемая при наращении платежей, из которых состоит рента.

Поскольку условия финансовых сделок весьма разнообразны, постольку разнообразны и виды потоков платежей. В основе классификации финансовых рент положены различные качественные признаки:

· В зависимости от периода продолжительности ренты выделяют

ü годовую ренту, которые представляют собой ежегодные платежи, т.е. период ренты равен 1 году;

ü срочную ренту, при которой период ренты может быть как более, так и менее года.

· По числу начислений процентов различают

ü ренты с начислением 1 раз в год;

ü ренты с начислением m раз в год;

o непрерывное начисление.

· По величине членов ренты могут быть

o постоянные ренты, где величина каждого отдельного платежа постоянна, т.е. рента с равными членами;

o переменные ренты, где величина платежа варьирует, т.е. рента с неравными членами.

· По числу членов ренты они бывают

o с конечным числом членов (ограниченные ренты), когда число членов ренты конечно и заранее известно;

o с бесконечным числом (вечные ренты), когда число ее членов заранее не известно.

· По вероятности выплаты ренты делятся на

o верные ренты, которые подлежат безусловной выплате, т.е. не зависят не от каких условий, например, погашение кредита;

o условные ренты, которые зависят от наступления некоторого случайного события.

· По методу выплаты платежей выделяют

o обычные ренты, которые на практике встречаются чаще всего,– с выплатой платежа в конце периода ренты (постнумерандо);

o ренты, с выплатой в начале периода ренты (пренумерандо).

Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т.п.

Рис. 7. Логика финансовой операции наращения финансовой ренты.

Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом равным R и множителем равным (1 + i).

Рассмотрим определение наращенной суммы на примере наиболее простого случая, – годовой постоянной обычной ренты:

где FVA – наращенная сумма ренты;

R – размер члена ренты, т.е. размер очередного платежа;

i – годовая процентная ставка, по которой на платежи начисляются сложные проценты;

n – срок ренты в годах,

s _n; i – коэффициент наращения ренты.