Пример Найдите ранг матрицы 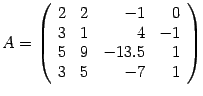 .
.
Решение. Первую строку оставляем без изменений. Чтобы избежать появления дробей, умножим вторую, третью и четвертую строки на 2:
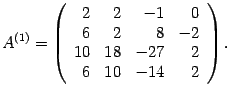
Первую строку умножим на 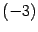 и прибавим ко второй. Получим строку
и прибавим ко второй. Получим строку  . Первую строку умножим на
. Первую строку умножим на 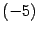 и прибавим к третьей. Получим строку
и прибавим к третьей. Получим строку 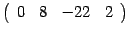 . Первую строку умножим на
. Первую строку умножим на 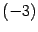 и прибавим к четвертой. Получим строку
и прибавим к четвертой. Получим строку 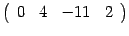 . В итоге имеем матрицу
. В итоге имеем матрицу
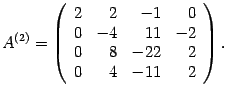
Вторую строку оставляем без изменений. К третьей строке прибавляем вторую, умноженную на 2. Получим строку 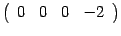 . К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид
. К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид
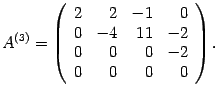
Поменяем местами третий и четвертый столбцы:
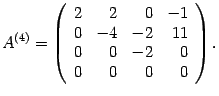
Базисный минор матрицы 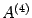 стоит в первых трех столбцах и первых трех строках,
стоит в первых трех столбцах и первых трех строках,  . Следовательно,
. Следовательно,  .
.
Пример Пусть

Найдём частные производные второго порядка. Для этого сначала найдём производные первого порядка:
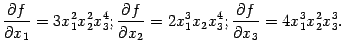
Затем находим производные от 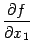 :
:
производные от 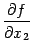 :
:
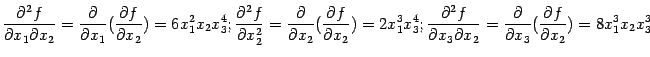
и производные от 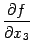 :
:
От любой из частных производных второго порядка можно рассматривать, в свою очередь, частные производные:
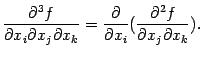
Эти производные (их 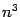 штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка
штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка
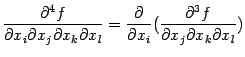
и т. д.
Если при вычислении частной производной высокого порядка некоторые дифференцирования проводятся по одной и той же переменной несколько раз подряд, то это отражается в обозначениях очевидным образом, например, 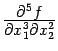 означает то же самое, что
означает то же самое, что  Дифференциальное и интегральное исчисление
Дифференциальное и интегральное исчисление
Многочисленные лотереи и страховые компании, которые организовались в течение этого периода, вызвали у многих математиков, включая Эйлера, интерес к теории вероятностей. Это повело к попыткам применить учение о вероятностях в новых областях.
5)Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
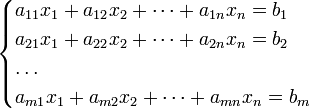
| (1)
|
Здесь x 1, x 2, …, xn — неизвестные, которые надо определить. a 11, a 12, …, amn — коэффициенты системы — и b 1, b 2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].
Система (1) называется однородной, если все её свободные члены равны нулю (b 1 = b 2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c 1, c 2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c 1(1), c 2(1), …, cn (1) и c 1(2), c 2(2), …, cn (2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
| c 1(1) = c 1(2), c 2(1) = c 2(2), …, cn (1) = cn (2).
|
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Содержание
[убрать]
- 1 Матричная форма
- 2 Методы решения
- 2.1 Прямые методы
- 2.2 Итерационные методы
- 3 См. также
- 4 Ссылки
- 5 Примечания
|
Матричная форма
Система линейных уравнений может быть представлена в матричной форме как:

или:
A x = B.
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Методы решения
Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
6)Основные понятия систем линейных уравнений
Системы линейных уравнений: основные понятия
24 июня 2011
Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
Определение. Решение системы уравнений — это последовательность чисел (k1, k2,..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2,..., xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Определение. Переменная xi называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x1, x3 и x4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x1, x3 и x5. Достаточно переписать самое последнее уравнение в виде x5 = x4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x1 = b1, x2 = b2,..., xk = bk;
- Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x2, x5, x6 (для первой системы) и x2, x5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Теорема. Если в системе из n уравнений переменные x1, x2,..., xr — разрешенные, а xr + 1, xr + 2,..., xk — свободные, то:
- Если задать значения свободным переменным (xr + 1 = tr + 1, xr + 2 = tr + 2,..., xk = tk), а затем найти значения x1, x2,..., xr, получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
7)Метод Крамера. Решение систем линейных уравнений
Метод Крамера
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Содержание
[убрать]
- 1 Описание метода
- 2 Пример
- 3 Вычислительная сложность
- 4 Примечания
|
[править] Описание метода
Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b 1, b 2,..., bn и x 1, x 2,..., xn, либо набор c 1, c 2,..., cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Пример
Система линейных уравнений:

Определители:
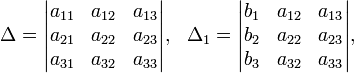

Решение:

Пример:

Определители:



8)Метод Гауса. Решение систем линейных уравнений
Ме́тод Га́усса [1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Описание метода
Пусть исходная система выглядит следующим образом
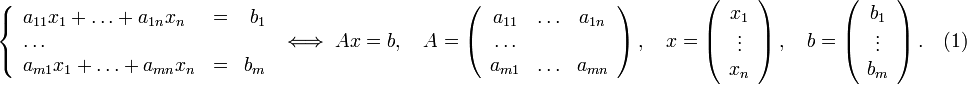
Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  [3].
[3].
Тогда переменные  называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число 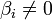 , где i > r, то рассматриваемая система несовместна.
, где i > r, то рассматриваемая система несовместна.
Пусть  для любых i > r.
для любых i > r.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом  (
( , где
, где  — номер строки):
— номер строки):
 ,
,
где 
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
9)Понятие вектора. Операции над векторами
Определение: Направленный отрезок (или упорядоченная пара точек) называется вектором.

Вектор обычно обозначается символом  , где А – начало, а В – конец направленного отрезка, либо одной буквой
, где А – начало, а В – конец направленного отрезка, либо одной буквой  (в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения.
(в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения.
Расстояние между началом и концом вектора называется его длиной. Для обозначения длины вектора (его абсолютной величины) пользуются символом модуля. Так  и
и  обозначают длины соответствующих векторов.
обозначают длины соответствующих векторов.
Вектор единичной длины называют ортом.
К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Считается, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет обозначать нулевой вектор вещественным числом 0 (нуль).
Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. Среди коллениарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы.
Векторы называются компланарными, если они лежат либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости.

Определение: Два вектора называются равными, если они: 1) коллинеарны; 2) равны по длине; 3) одинаково направлены.
Следствие: Для любого вектора  и для любой точки А, существует, и притом единственная, точка B такая, что
и для любой точки А, существует, и притом единственная, точка B такая, что  .
.
Мы не будем различать двух равных векторов, имеющих разные точки приложения. Такие векторы называются свободными (в отличие от скользящих и связанных векторов, встречающихся в других науках).
Понятие равенства векторов обладает следующими свойствами:
1.  (рефлексивность).
(рефлексивность).
2. Из того, что  , следует
, следует  (симметричность).
(симметричность).
3. Из того, что  и
и  , следует
, следует  (транзитивность).
(транзитивность).
Глава 2. Операции над векторами

Определение: Суммой  двух векторов и называется вектор, имеющий начало в начале вектора
двух векторов и называется вектор, имеющий начало в начале вектора  , а конец – в конце вектора
, а конец – в конце вектора 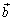 , при условии, что вектор
, при условии, что вектор 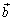 приложен к концу вектора
приложен к концу вектора  .
.
В соответствии с определением слагаемые  и
и 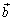 и их сумма
и их сумма  образуют треугольник (рис.2). Поэтому данное правило сложения двух векторов называют «правилом треугольника».
образуют треугольник (рис.2). Поэтому данное правило сложения двух векторов называют «правилом треугольника».
Операция сложения векторов обладает свойствами:
1. 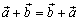 (коммутативность);
(коммутативность);
2.  , (ассоциативность);
, (ассоциативность);
3.  для любого вектора
для любого вектора  (особая роль нулевого вектора);
(особая роль нулевого вектора);
4. для каждого вектора  существует противоположный ему вектор
существует противоположный ему вектор  такой, что
такой, что  (для получения
(для получения  достаточно поменять местами начало и конец вектора
достаточно поменять местами начало и конец вектора  ).
).
Вектор противоположный вектору  обозначают
обозначают  .
.
Определение: Разностью  векторов
векторов  и
и 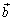 называется сумма вектора
называется сумма вектора  и вектора противоположного вектору
и вектора противоположного вектору 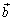 , т.е.
, т.е. 
 .
.
Разность  получается из вектора
получается из вектора  сдвигом его начала в конец вектора
сдвигом его начала в конец вектора 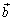 , при условии, что векторы
, при условии, что векторы  и
и 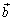 имеют общее начало (рис.3). Очевидно, что
имеют общее начало (рис.3). Очевидно, что  для любого вектора
для любого вектора  .
.
Замечание: Существует еще одно правило сложения векторов, называемое «правилом параллелограмма»: векторы  и
и 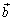 прикладываются к общему началу О, и на них строится параллелограмм (рис. 4). Суммой
прикладываются к общему началу О, и на них строится параллелограмм (рис. 4). Суммой  будет вектор
будет вектор  , расположенный на диагонали параллелограмма. Разностью
, расположенный на диагонали параллелограмма. Разностью  здесь будет вектор
здесь будет вектор  , расположенный на второй диагонали.
, расположенный на второй диагонали.
 Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами.
Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами.
Определение: Произведением  вектора
вектора  на вещественное число λ (скаляр) называется вектор
на вещественное число λ (скаляр) называется вектор 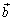 , такой, что 1)
, такой, что 1)  ; 2) вектор
; 2) вектор 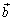 коллинеарен вектору
коллинеарен вектору  ; 3) векторы
; 3) векторы  и
и 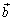 имеют одинаковое (противоположное) направление если λ > 0 (λ < 0).
имеют одинаковое (противоположное) направление если λ > 0 (λ < 0).
Замечание: В случае, когда λ = 0 или  произведение
произведение  является нулевым вектором.
является нулевым вектором.
Операция умножения вектора на число обладает следующими свойствами:
1.  (ассоциативное свойство сомножителей);
(ассоциативное свойство сомножителей);

Действительно, заметим, что векторы, стоящие обеих частях равенства, имеют одну и ту же длину  . Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением
. Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением  , если λ и μ одного знака, и противоположно направлению
, если λ и μ одного знака, и противоположно направлению  , если λ и μ имеют разные знаки. Если же λ или μ равны нулю, то обе части равенства равны нулю. Свойство доказано.
, если λ и μ имеют разные знаки. Если же λ или μ равны нулю, то обе части равенства равны нулю. Свойство доказано.

2. 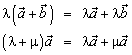 (свойства дистрибутивности).
(свойства дистрибутивности).


Построим треугольник OAB где  и
и  . Построим далее треугольник SPQ, где
. Построим далее треугольник SPQ, где  и
и  . Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что
. Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что  и
и  одинаково направлены, если λ > 0. Отсюда следует, что
одинаково направлены, если λ > 0. Отсюда следует, что  . Но
. Но  и
и  , а отсюда вытекает первое свойство дистрибутивности.
, а отсюда вытекает первое свойство дистрибутивности.
Очевидно, что векторы стоящие в обеих частях второго свойства дистрибутивности коллинеарны. Допустим сначала, что знаки λ и μ одинаковы. Тогда векторы  и
и  направлены одинаково и длина их суммы равна сумме их длин, т. е.
направлены одинаково и длина их суммы равна сумме их длин, т. е.  . Но
. Но  и следовательно, в этом случае векторы
и следовательно, в этом случае векторы  и
и  равны по длине. Направление их совпадает с направлением вектора
равны по длине. Направление их совпадает с направлением вектора  , если общий знак λ и μ положителен, и противоположно ему, если отрицателен. Допустим теперь, что знаки λ и μ различны, и для определенности будем считать |λ| > |μ|. В этом случае длина суммы равна разности длин, точнее
, если общий знак λ и μ положителен, и противоположно ему, если отрицателен. Допустим теперь, что знаки λ и μ различны, и для определенности будем считать |λ| > |μ|. В этом случае длина суммы равна разности длин, точнее  . Но
. Но  . Следовательно, и в этом случае длина вектора
. Следовательно, и в этом случае длина вектора  равна длине вектора
равна длине вектора  . Очевидно, что оба эти вектора направлены так же, как
. Очевидно, что оба эти вектора направлены так же, как  . Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор
. Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор  или оба скаляра одновременно.
или оба скаляра одновременно.
10)Вектора в прямоугольной декартовой системе координат
11)Уравнение прямой на плоскости



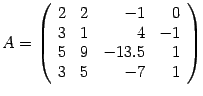 .
.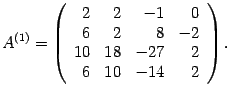
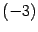 и прибавим ко второй. Получим строку
и прибавим ко второй. Получим строку  . Первую строку умножим на
. Первую строку умножим на 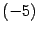 и прибавим к третьей. Получим строку
и прибавим к третьей. Получим строку 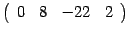 . Первую строку умножим на
. Первую строку умножим на 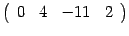 . В итоге имеем матрицу
. В итоге имеем матрицу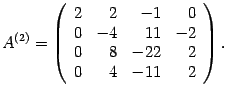
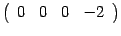 . К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид
. К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид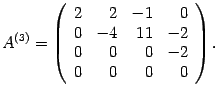
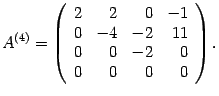
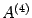 стоит в первых трех столбцах и первых трех строках,
стоит в первых трех столбцах и первых трех строках,  . Следовательно,
. Следовательно,  .
.
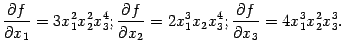
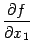 :
:

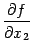 :
: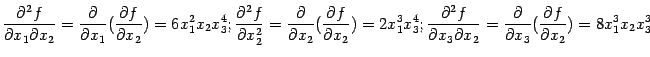
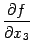 :
: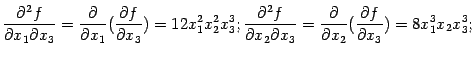
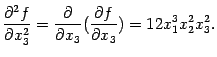
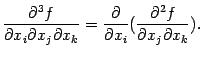
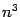 штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка
штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка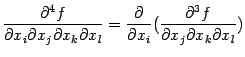
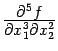 означает то же самое, что
означает то же самое, что  Дифференциальное и интегральное исчисление
Дифференциальное и интегральное исчисление 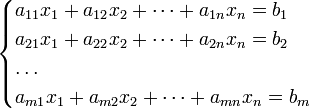







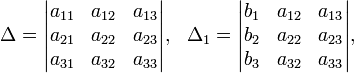






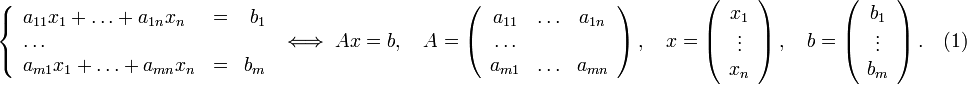

 [3].
[3].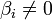 , где i > r, то рассматриваемая система несовместна.
, где i > r, то рассматриваемая система несовместна. для любых i > r.
для любых i > r. (
( , где
, где  — номер строки):
— номер строки): ,
,

 , где А – начало, а В – конец направленного отрезка, либо одной буквой
, где А – начало, а В – конец направленного отрезка, либо одной буквой  (в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения.
(в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения. и
и  обозначают длины соответствующих векторов.
обозначают длины соответствующих векторов.
 .
. (рефлексивность).
(рефлексивность). , следует
, следует  (симметричность).
(симметричность). , следует
, следует  (транзитивность).
(транзитивность).
 двух векторов и называется вектор, имеющий начало в начале вектора
двух векторов и называется вектор, имеющий начало в начале вектора  , а конец – в конце вектора
, а конец – в конце вектора 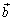 , при условии, что вектор
, при условии, что вектор 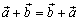 (коммутативность);
(коммутативность); , (ассоциативность);
, (ассоциативность); для любого вектора
для любого вектора  такой, что
такой, что  (для получения
(для получения  .
. векторов
векторов 
 .
. для любого вектора
для любого вектора  , расположенный на диагонали параллелограмма. Разностью
, расположенный на диагонали параллелограмма. Разностью  , расположенный на второй диагонали.
, расположенный на второй диагонали. Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами.
Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами. вектора
вектора  ; 2) вектор
; 2) вектор  произведение
произведение  (ассоциативное свойство сомножителей);
(ассоциативное свойство сомножителей);
 . Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением
. Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением 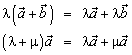 (свойства дистрибутивности).
(свойства дистрибутивности). 
 и
и  . Построим далее треугольник SPQ, где
. Построим далее треугольник SPQ, где  и
и  . Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что
. Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что  и
и  одинаково направлены, если λ > 0. Отсюда следует, что
одинаково направлены, если λ > 0. Отсюда следует, что  . Но
. Но  и
и  , а отсюда вытекает первое свойство дистрибутивности.
, а отсюда вытекает первое свойство дистрибутивности. направлены одинаково и длина их суммы равна сумме их длин, т. е.
направлены одинаково и длина их суммы равна сумме их длин, т. е.  . Но
. Но  и следовательно, в этом случае векторы
и следовательно, в этом случае векторы  и
и  равны по длине. Направление их совпадает с направлением вектора
равны по длине. Направление их совпадает с направлением вектора  . Но
. Но  . Следовательно, и в этом случае длина вектора
. Следовательно, и в этом случае длина вектора  . Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор
. Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор 


