Числовая последовательность { a n } называется ограниченной сверху, если все ее члены меньше некоторого числа А:
a n < А (п = 1, 2, 3,...).
Примером такой последовательности может служить последовательность
1/2, 2/3, 3/4,..., n / n +1,...,
все члены которой меньше 1:
a n < 1.
Здесь в роли А выступает число 1. Вместо него можно было бы выбрать 2, 3, 5/2 и т. д., поскольку любое число рассматриваемой последовательности меньше каждого из этих чисел. Важно не то, какое число выбрано в качестве А, а то, что хотя бы одно такое число существует.
Важным примером последовательности, ограниченной сверху, служит последовательность
p 4, p 8, p 16, p 32,... (1)
периметров правильных 4-, 8-, 16-угольников и т. д., вписанных в одну и ту же окружность. Для доказательства ограниченности этой последовательности мы поступим следующим образом. Наряду с данной последовательностью рассмотрим последовательность
Р4, Р8, Р16, Р32,... (2)
периметров правильных 4-, 8-, 16-угольников и т. д., описанных около той же самой окружности. Очевидно, что сторона АВ правильного 2 n -угольника, вписанного в окружность, меньше стороны А'В' правильного 2 n -угольника, описанного около этой окружности (рис. 200).

Поэтому
p 2 n < Р2 n (3)
Как было отмечено в предыдущем параграфе, последовательность (2) является монотонно убывающей. Поэтому каждый член этой последовательности, начиная со второго, меньше первого члена Р4. Следовательно, для любого п > 2
P2 n < Р4 (4)
Из (3) и (4) вытекает, что
p 2 n < Р4
Но Р4 = 8 r, где r — радиус окружности. Итак, для всех п >2
p 2 n < 8 r.
Это неравенство и говорит о том, что последовательность (1) ограничена сверху. Роль А в данном случае играет число 8 r.
Если члены ограниченной сверху числовой последовательности изобразить точками числовой прямой, эти все точки расположатся левее точки с абсциссой А (рис. 201).

Числовая последовательность { a n } называется ограниченной снизу, если все ее члены больше некоторого числа В:
a n > В (п = 1, 2, 3,...).
Примером такой последовательности может служить натуральный ряд чисел
1, 2, 3, 4, 5.....
Он ограничен снизу, так как все его члены больше нуля (В = 0). В качестве В можно было бы указать и любое отрицательное число или 1/2, 1/3 и т.д. Как и в случав последовательности, ограниченной сверху, здесь важно не то, какое число выбрать в качестве В, а то, что хотя бы одно такое число существует.
Важным примером последовательности, ограниченной снизу, является последовательность
Р4, Р8, Р16,...
периметров правильных 4-, 8-, 16-угольников и т. д., описанных около окружности. В этом легко убедиться с помощью рассуждений, аналогичных тем, которые мы проводили выше при исследовании последовательности
p 4, p 8, p 16,...
Если члены ограниченной снизу числовой последовательности изобразить точками числовой прямой, то все точки расположатся правее точки с абсциссой В (рис. 202).

Числовая последовательность, ограниченная одновременно и снизу и сверху, называется ограниченной.
Другими словами, числовая последовательность a 1, a 2,..., a n,... называется ограниченной, если существуют числа А и В такие, что при любом п
А < a n < В (п = 1, 2, 3,...).
Очевидно, что все точки числовой оси, соответствующие членам такой числовой последовательности, заключены в отрезке, концы которого имеют абсциссы А и В (рис. 203).

Примеры.
1) sin 1, sin 2, sin 3,..., sin n.....
Для этой последовательности a n = sin п. При любом п
—2 <sin n < 2.
Поэтому данная числовая последовательность ограничена.
2) 1,4; 1,41; 1,414; 1,4142;....
Члены этой последовательности представляют собой десятичные приближения числа √2. Очевидно, что 1 < a n < 2, так что эта последовательность также ограничена.
3) Ограниченными будут, очевидно, и рассмотренные выше последовательности:
p 4, p 8, p 16, p 32,...
Р4, Р8, Р16, Р32,...
составленные из периметров правильных 2 n -угольников, вписанных и описанных около некоторой окружности.
22 вопрос
Бесконечно малая величина
Последовательность  называется бесконечно малой, если
называется бесконечно малой, если  . Например, последовательность чисел
. Например, последовательность чисел 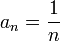 — бесконечно малая.
— бесконечно малая.
Функция называется бесконечно малой в окрестности точки  , если
, если 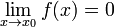 .
.
Функция называется бесконечно малой на бесконечности, если  либо
либо  .
.
Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то
, то  ,
,  .
.
Свойства бесконечно малых
- Сумма конечного числа бесконечно малых — бесконечно малая.
- Произведение бесконечно малых — бесконечно малая.
- Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
- Если
 — бесконечно малая последовательность, сохраняющая знак, то
— бесконечно малая последовательность, сохраняющая знак, то  — бесконечно большая последовательность.
— бесконечно большая последовательность.
23 вопрос
Определение
Число  называется пределом числовой последовательности
называется пределом числовой последовательности 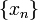 , если последовательность
, если последовательность  является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.
, её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

Частичный предел последовательности — это предел одной изеёподпоследовательностей.
Верхний предел последовательности — это наибольшая из её предельных точек.
Нижний предел последовательности — это наименьшая из её предельных точек.
Обозначения
Тот факт, что последовательность 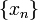 сходится к числу
сходится к числу  обозначается одним из следующих способов:
обозначается одним из следующих способов:
-
 ;
;
-
 .
.
Свойства
Существуют определённые особенности для предела последовательностей вещественных чисел.[2]
Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств.
Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела.
Свойства
Арифметические свойства
- Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
- Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.

- Однородность. Константу можно выносить из-под знака предела.

- Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

- Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.

Свойства сохранения порядка
- Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.

- Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.

- Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.
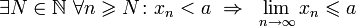
- Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.

- Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.

- Для числовых последовательностей справедлива теорема о двух милиционерах (принцип двустороннего ограничения).

Другие свойства
- Сходящаяся числовая последовательность имеет только один предел.

- Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.
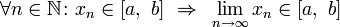
- Предел последовательности из одного и того же числа равен этому числу.
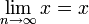
- Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел.
- У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.
- Имеет место теорема Штольца.
- Если у последовательности
 существует предел, то последовательность средних арифметических
существует предел, то последовательность средних арифметических  имеет тот же предел (следствие из теоремы Штольца).
имеет тот же предел (следствие из теоремы Штольца).
- Если у последовательности чисел
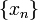 существует предел
существует предел  , и если задана функция
, и если задана функция  , определенная для каждого
, определенная для каждого  и непрерывная в точке
и непрерывная в точке  , то
, то

24 вопрос







 называется бесконечно малой, если
называется бесконечно малой, если  . Например, последовательность чисел
. Например, последовательность чисел 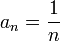 — бесконечно малая.
— бесконечно малая. , если
, если 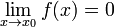 .
. либо
либо  .
. , то
, то  ,
,  .
. — бесконечно большая последовательность.
— бесконечно большая последовательность. называется пределом числовой последовательности
называется пределом числовой последовательности 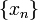 , если последовательность
, если последовательность  является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
 , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.
, её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.


 ;
; .
.





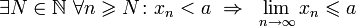




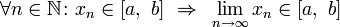
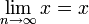
 существует предел, то последовательность средних арифметических
существует предел, то последовательность средних арифметических  имеет тот же предел (следствие из теоремы Штольца).
имеет тот же предел (следствие из теоремы Штольца). , и если задана функция
, и если задана функция  , определенная для каждого
, определенная для каждого 



