1. Математическое ожидание неслучайного процесса j(t) равно самому неслучайному процессу:
 . (1.9)
. (1.9)
Из выражения (1.9) следует, что любая центрированная неслучайная функция равна нулю, поскольку
 . (1.10)
. (1.10)
2. Если случайная величина Y (t) представляет собой линейную комбинацию функций Xi (t):
 , (1.11)
, (1.11)
где  - неслучайные функции t, то
- неслучайные функции t, то
 . (1.12)
. (1.12)
Последнее соотношение следует из того, что операция определения математического ожидания линейна.
3. Корреляционная функция неслучайного процесса тождественно равна нулю. Это свойство следует непосредственно из (1.10).
4. Корреляционная функция не изменяется от прибавления к случайной функции любой неслучайной функции  . Действительно, если
. Действительно, если  , то
, то

и
 . (1.13)
. (1.13)
Отсюда следует, что корреляционные функции случайных процессов  и
и
 совпадают. Поэтому при определении корреляционных функций всегда можно считать, что рассматриваемый процесс является центрированным.
совпадают. Поэтому при определении корреляционных функций всегда можно считать, что рассматриваемый процесс является центрированным.
5. Если случайный процесс Y (t) представляет собой линейную комбинацию случайных процессов Xi (t):
 ,
,
где  - неслучайные функции, то
- неслучайные функции, то
 , (1.14)
, (1.14)
где 
 - собственная корреляционная функция процесса Xi (t),
- собственная корреляционная функция процесса Xi (t),  - взаимная корреляционная функция процессов
- взаимная корреляционная функция процессов  и
и  .
.
Действительно:
 ,
,  =
=
= 
 .
.
 Если случайные процессы
Если случайные процессы  попарно некоррелированы, то
попарно некоррелированы, то
 . (1.15)
. (1.15)
Полагая в (1.14)  , получим выражение для дисперсии линейной комбинации случайных процессов:
, получим выражение для дисперсии линейной комбинации случайных процессов:
 . (1.16)
. (1.16)
В частном случае некоррелированных случайных процессов 
 . (1.17)
. (1.17)
6. Корреляционная функция является неотрицательно определенной функцией:
 . (1.18)
. (1.18)
Действительно, представим (1.18) в виде:
 .
.
Так как интеграл есть предел интегральной суммы, то последнее выражение можно представить в виде предела суммы математических ожиданий, которая, в свою очередь, равна математическому ожиданию суммы. Поэтому операции интегрирования и математического ожидания можно менять местами. В результате получим:

7. Корреляционная функция симметрична относительно своих аргументов. Взаимная корреляционная функция этим свойством не обладает.
Симметричность корреляционной функции вытекает непосредственно из её определения:
 . (1.19)
. (1.19)
В то же время для взаимной корреляционной функции имеем:
 .
.
Взаимная корреляционная функция удовлетворяет следующему соотношению:
 . (1.20)
. (1.20)
8. Корреляционная функция и взаимная корреляционная функция удовлетворяют следующим неравенствам:
 , (1.21)
, (1.21)
 . (1.22)
. (1.22)
Часто вместо собственной и взаимной корреляционных функций рассматривают нормированные корреляционные функции:
 , (1.23)
, (1.23)
 . (1.24)
. (1.24)
Нас основании (1.21) и (1.22) для нормированных корреляционных функций справедливы неравенства:

 . (1.25)
. (1.25)
Пример Заданный случайных процесс представляет собой сумму случайного и неслучайного процессов:  . Заданы
. Заданы  , определить
, определить 
Используя (1.9) и (1.12), будем иметь:
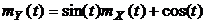 .
.
Согласно (1.15)

и, наконец, в соответствии с (1.17)  .
.
КЛАССИФИКАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Стационарные процессы
Случайный процесс называется стационарным, если его многомерный закон распределения зависит лишь от взаимного расположения моментов времени t 1, t 2,... tn, т.е. не меняется при одновременном сдвиге этих моментов времени на одинаковые величины:
 . (2.1)
. (2.1)
Если выражение (2.1) удовлетворяется при любом n, то такой процесс называется стационарным в узком смысле.
При n =1 выражение (2.1) приобретает вид:
 и при
и при 
 , 2.2)
, 2.2)
т.е. одномерный закон распределения стационарного процесса не зависит от времени. Следовательно, от времени не будут зависеть и характеристики случайного процесса, зависящие от одномерного закона распределения: математическое ожидание и дисперсия случайного процесса:
 ,
,  . (2.3)
. (2.3)
При n =2 выражение (2.1) переписывается следующим образом:
 и при
и при 

 , (2.4)
, (2.4)
где  .
.
Следовательно корреляционная функция стационарного процесса, определяемая двумерным законом распределения, будет зависеть лишь от интервала времени t
 . (2.5)
. (2.5)
По определению А.Я.Хинчина процесс является стационарным в широком смысле, если условие стационарности (2.1) удовлетворяется лишь при n= 1 и 2.
Следовательно, условия стационарности процесса в широком смысле можно сформулировать в виде:
· математическое ожидание и дисперсия такого процесса не зависят от времени -  и DX;
и DX;
· корреляционная функция процесса зависит лишь от интервала между сечениями по времени -  .
.
KXX (t) является четной функцией своего аргумента:
 . (2.6)
. (2.6)
При решении практических задач часто применяются следующие аппроксимации
KXX (t):
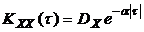



Следует помнить, что взаимная корреляционная функция представляет собой нечетную функцию:
 , (
, ( ). (2.7)
). (2.7)
Нормальные процессы
Случайный процесс является нормальным, если нормальным является любой многомерный закон:

×  ), (2.8)
), (2.8)
где  (2.9)
(2.9)
 - относительные собственные и взаимные корреляционные функции,
- относительные собственные и взаимные корреляционные функции,
 - алгебраическое дополнение определителя (2.9), отвечающее элементу
- алгебраическое дополнение определителя (2.9), отвечающее элементу
матрицы  .
.
Если  и
и  отвечают свойствам стационарности и процесс нормален, то и
отвечают свойствам стационарности и процесс нормален, то и  также отвечают свойствам стационарности. Следовательно, для нормального процесса понятия стационарности в узком и широком смыслах совпадают.
также отвечают свойствам стационарности. Следовательно, для нормального процесса понятия стационарности в узком и широком смыслах совпадают.
Эргодические процессы
Стационарный процесс является эргодическим, если любая его характеристика, полученная усреднением множества реализаций, совпадает с результатами усреднения за достаточно большой интервал одной реализации, т.е.
 ,
,  , (2.10)
, (2.10)
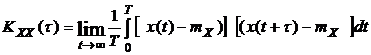 . (2.11)
. (2.11)
В случае эргодического процесса справедливо следующее соотношение:
 (
( ). (2.12)
). (2.12)
Приведем пример стационарного, но не эргодического процесса. Пусть
 , (2.13)
, (2.13)
где X (t) – эргодический процесс, Y – случайная величина. Определим  .
.

 +
+  . (2.14)
. (2.14)
Поскольку  , то случайный процесс
, то случайный процесс  не является эргодическим, хотя и сохраняет стационарность.
не является эргодическим, хотя и сохраняет стационарность.
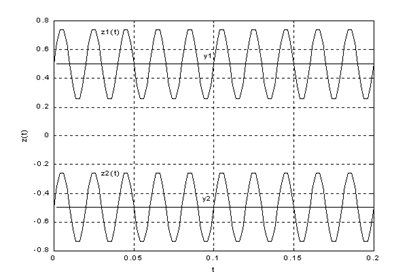
Действительно, различные реализации этого процесса имеют разные характеристики. На рис.2.1 приведены две реализации случайного процесса при  и двух значениях случайной величины Y – y 1 и y 2. Из рисунка видно, что математическое ожидание реализации при Y = y 1 равно y 1, а при Y = y 2 – y 2.
и двух значениях случайной величины Y – y 1 и y 2. Из рисунка видно, что математическое ожидание реализации при Y = y 1 равно y 1, а при Y = y 2 – y 2.
Рис.2.1. Пример стационарного неэргодического процесса
Таким образом, по единственной реализации стационарного, но неэргодического процесса нельзя судить о характеристиках процесса в целом.
Марковские процессы
Если вероятностные свойства случайного процесса полностью определяются значением его ординаты в заданный момент времени и не зависят от значений ординат процесса в предыдущие моменты времени, то такой случайный процесс называется Марковским. Иногда такие процессы называют процессами без последействия.



 . (1.9)
. (1.9) . (1.10)
. (1.10) , (1.11)
, (1.11) - неслучайные функции t, то
- неслучайные функции t, то . (1.12)
. (1.12) . Действительно, если
. Действительно, если  , то
, то
 . (1.13)
. (1.13) и
и совпадают. Поэтому при определении корреляционных функций всегда можно считать, что рассматриваемый процесс является центрированным.
совпадают. Поэтому при определении корреляционных функций всегда можно считать, что рассматриваемый процесс является центрированным. , (1.14)
, (1.14)
 - собственная корреляционная функция процесса Xi (t),
- собственная корреляционная функция процесса Xi (t),  - взаимная корреляционная функция процессов
- взаимная корреляционная функция процессов  и
и  .
. ,
,  =
=
 .
. Если случайные процессы
Если случайные процессы  попарно некоррелированы, то
попарно некоррелированы, то . (1.15)
. (1.15) , получим выражение для дисперсии линейной комбинации случайных процессов:
, получим выражение для дисперсии линейной комбинации случайных процессов: . (1.16)
. (1.16) . (1.17)
. (1.17) . (1.18)
. (1.18) .
.
 . (1.19)
. (1.19) .
. . (1.20)
. (1.20) , (1.21)
, (1.21) . (1.22)
. (1.22) , (1.23)
, (1.23) . (1.24)
. (1.24)
 . (1.25)
. (1.25) . Заданы
. Заданы  , определить
, определить 
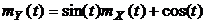 .
.
 .
. . (2.1)
. (2.1) и при
и при 
 , 2.2)
, 2.2) ,
,  . (2.3)
. (2.3) и при
и при 

 , (2.4)
, (2.4) .
. . (2.5)
. (2.5) и DX;
и DX; .
. . (2.6)
. (2.6)

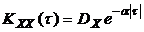





 , (
, ( ). (2.7)
). (2.7)
 ), (2.8)
), (2.8) (2.9)
(2.9) - относительные собственные и взаимные корреляционные функции,
- относительные собственные и взаимные корреляционные функции, - алгебраическое дополнение определителя (2.9), отвечающее элементу
- алгебраическое дополнение определителя (2.9), отвечающее элементу .
. и
и  отвечают свойствам стационарности и процесс нормален, то и
отвечают свойствам стационарности и процесс нормален, то и  также отвечают свойствам стационарности. Следовательно, для нормального процесса понятия стационарности в узком и широком смыслах совпадают.
также отвечают свойствам стационарности. Следовательно, для нормального процесса понятия стационарности в узком и широком смыслах совпадают. ,
,  , (2.10)
, (2.10)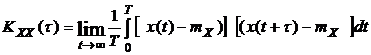 . (2.11)
. (2.11) (
( ). (2.12)
). (2.12) , (2.13)
, (2.13) .
.
 +
+  . (2.14)
. (2.14) , то случайный процесс
, то случайный процесс  и двух значениях случайной величины Y – y 1 и y 2. Из рисунка видно, что математическое ожидание реализации при Y = y 1 равно y 1, а при Y = y 2 – y 2.
и двух значениях случайной величины Y – y 1 и y 2. Из рисунка видно, что математическое ожидание реализации при Y = y 1 равно y 1, а при Y = y 2 – y 2.