Д.У. в моделировании процессов. Примеры.
При решении различных задач в математике, физике и т.д мы можем пользоваться матем моделями в виде спец ДУ. В таких задачах требуется найти зависимость между переменными величинами
Нахождение общего решения Д.У. с помощью рядов.
Решения многих дифференциальных уравнений не выражаются в элементарных функциях. В этих случаях пользуются приближенными методами интегрирования дифференциальных уравнений. Одним из таких методов является представление решения уравнения в виде степенного ряда; сумма конечного числа членов этого ряда будет приближенно равна искомому решению. Указанный степенной ряд находят способом неопределенных коэффициентов или способом, основанным на применении ряда Тейлора (Маклорена).
Способ неопределенных коэффициентов особенно удобен в применении к линейным уравнениям, т. е. уравнениям вида
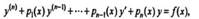
И состоит в следующем. Если все коэффициенты этого равнения и свободный член разлагаются в ряды по степеням, сходящиеся в интервале, то искомое решениеТакже представляется степенным рядом
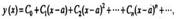
Сходящимся в этом же интервале. Подставляя в уравнение функцию и ее производные, приравнивают коэффициенты при одинаковых степенях. Из полученных при этом уравнений и заданных начальных условий находят коэффициенты
Способ основанный на применение ряда Тейлора (Маклорена), заключается в последовательном дифференцировании данного уравнения. Это дает возможность найти значения производных, входящих в выражения для коэффициентов ряда
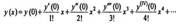
Являющегося решением уравнения.
Д.У. естественного роста
Дифференциальное уравнение вида (6.1)при x(t) > 0 и постоянном (отрицательном или положительном) k легко решается путем разделения переменных и последующим интегрированием: ∫1/xdx=∫kdx⇒ ln x = kt + C.
Затем мы решаем его относительно х: e^ ln x=e^ (kt + C); ⇒ x = x(t) = e^C*e^kt= Ae^kt, где А = е^C – константа.
А = х(0) = х0, так что частное решение уравнения (6.1) с начальным условием х(0)=х0 – это: x(t) = х0e^ kt
Решение уравнения содержит показательную функцию (с основанием, равным основанию натуральных логарифмов), а само дифференциальное уравнение: dx/dt = kх часто называют уравнением экспоненциального роста, или уравнением естественного роста. x(t) = х0e^ kt
Дифференциальное уравнение: dx/ dt= kx (k – константа) служит математической моделью для невероятно широкого диапазона естественных явлений – всех тех, в которых скорость изменения некоторой величины пропорциональна текущему значению. Рассмотрим некоторыепримеры. Прирост популяции.Предположим, что P(t) – численность популяции (людей, насекомых или бактерий), у которой постоянны показатели рождаемости и смертности β и δ (количество рождений и случаев смерти на определенное количество особей в единицу времени). Тогда в течение короткого временного интервала Δt происходит приблизительно βP(t)Δt рождений и δP(t)Δt случаев смерти, так что P(t) изменяется приблизительно на: ΔP(t) ≈ (β – δ)P(t)Δt и поэтому
dP/ dt= lim Δ P/ Δ t= kP
t Δ →0 где k = β – δ.
4.Д.У. 1ого порядка. Задача Коши. y’=f(x,y).(Теорема Каши).
Т: Если функция f(x,y) и 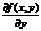 непрерывны в некоторой области D, содержащей точку Р0(х0,у0), то существует единственное решение уравнения y’=f(x,y) удовлетворяющее начальному условию
непрерывны в некоторой области D, содержащей точку Р0(х0,у0), то существует единственное решение уравнения y’=f(x,y) удовлетворяющее начальному условию 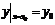 .
.
О: Дифференциальным уравнением I порядка называется уравнение, в которое входят независимая переменная х, неизвестная функция у, и её производная у’, т.е. это уравнение имеет вид F(x,y,y’)=0 (1)
Из уравнения (1) производную можно выразить через независимую переменную х и неизвестную функцию у, то дифференциал уравнения (1): y’=f(x,y)
Линейные неоднородные д.у.
Линейное неоднородное уравнение данного типа имеет вид:
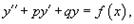
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
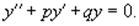
Теорема: Общее решение неоднородного уравнения является суммой общего решения y 0(x) соответствуюшего однородного уравнения и частного решения y 1(x) неоднородного уравнения:
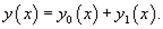
Д.У. консольной балки
Изгиб. Момнет М=М1+М2
М1-собст вес, М2-внешн. Силы,М-?
Для определения М надо вычислить элемент.∆М1
∆М1=∆tgt; М1≈∑∆М1
М1∫ qtdt=q*t*t/2=q/2(l-x*x)
∑M=EJ/R
E-модуль Юнга J-момент инерции попереч. сечения балки
R-радиус кривизны балки
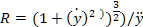
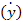 =tgα α=0
=tgα α=0 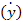 =0
=0
R=1/y^4 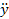 =1/ EJ-ДУ
=1/ EJ-ДУ
Д.У. в моделировании процессов. Примеры.
При решении различных задач в математике, физике и т.д мы можем пользоваться матем моделями в виде спец ДУ. В таких задачах требуется найти зависимость между переменными величинами
Нахождение общего решения Д.У. с помощью рядов.
Решения многих дифференциальных уравнений не выражаются в элементарных функциях. В этих случаях пользуются приближенными методами интегрирования дифференциальных уравнений. Одним из таких методов является представление решения уравнения в виде степенного ряда; сумма конечного числа членов этого ряда будет приближенно равна искомому решению. Указанный степенной ряд находят способом неопределенных коэффициентов или способом, основанным на применении ряда Тейлора (Маклорена).
Способ неопределенных коэффициентов особенно удобен в применении к линейным уравнениям, т. е. уравнениям вида
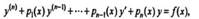
И состоит в следующем. Если все коэффициенты этого равнения и свободный член разлагаются в ряды по степеням, сходящиеся в интервале, то искомое решениеТакже представляется степенным рядом
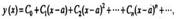
Сходящимся в этом же интервале. Подставляя в уравнение функцию и ее производные, приравнивают коэффициенты при одинаковых степенях. Из полученных при этом уравнений и заданных начальных условий находят коэффициенты
Способ основанный на применение ряда Тейлора (Маклорена), заключается в последовательном дифференцировании данного уравнения. Это дает возможность найти значения производных, входящих в выражения для коэффициентов ряда
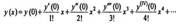
Являющегося решением уравнения.
Д.У. естественного роста
Дифференциальное уравнение вида (6.1)при x(t) > 0 и постоянном (отрицательном или положительном) k легко решается путем разделения переменных и последующим интегрированием: ∫1/xdx=∫kdx⇒ ln x = kt + C.
Затем мы решаем его относительно х: e^ ln x=e^ (kt + C); ⇒ x = x(t) = e^C*e^kt= Ae^kt, где А = е^C – константа.
А = х(0) = х0, так что частное решение уравнения (6.1) с начальным условием х(0)=х0 – это: x(t) = х0e^ kt
Решение уравнения содержит показательную функцию (с основанием, равным основанию натуральных логарифмов), а само дифференциальное уравнение: dx/dt = kх часто называют уравнением экспоненциального роста, или уравнением естественного роста. x(t) = х0e^ kt
Дифференциальное уравнение: dx/ dt= kx (k – константа) служит математической моделью для невероятно широкого диапазона естественных явлений – всех тех, в которых скорость изменения некоторой величины пропорциональна текущему значению. Рассмотрим некоторыепримеры. Прирост популяции.Предположим, что P(t) – численность популяции (людей, насекомых или бактерий), у которой постоянны показатели рождаемости и смертности β и δ (количество рождений и случаев смерти на определенное количество особей в единицу времени). Тогда в течение короткого временного интервала Δt происходит приблизительно βP(t)Δt рождений и δP(t)Δt случаев смерти, так что P(t) изменяется приблизительно на: ΔP(t) ≈ (β – δ)P(t)Δt и поэтому
dP/ dt= lim Δ P/ Δ t= kP
t Δ →0 где k = β – δ.
4.Д.У. 1ого порядка. Задача Коши. y’=f(x,y).(Теорема Каши).
Т: Если функция f(x,y) и 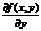 непрерывны в некоторой области D, содержащей точку Р0(х0,у0), то существует единственное решение уравнения y’=f(x,y) удовлетворяющее начальному условию
непрерывны в некоторой области D, содержащей точку Р0(х0,у0), то существует единственное решение уравнения y’=f(x,y) удовлетворяющее начальному условию 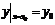 .
.
О: Дифференциальным уравнением I порядка называется уравнение, в которое входят независимая переменная х, неизвестная функция у, и её производная у’, т.е. это уравнение имеет вид F(x,y,y’)=0 (1)
Из уравнения (1) производную можно выразить через независимую переменную х и неизвестную функцию у, то дифференциал уравнения (1): y’=f(x,y)



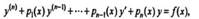
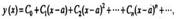
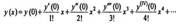
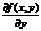 непрерывны в некоторой области D, содержащей точку Р0(х0,у0), то существует единственное решение уравнения y’=f(x,y) удовлетворяющее начальному условию
непрерывны в некоторой области D, содержащей точку Р0(х0,у0), то существует единственное решение уравнения y’=f(x,y) удовлетворяющее начальному условию 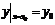 .
.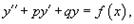
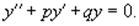
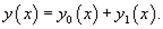
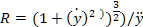
 =tgα α=0
=tgα α=0  =1/ EJ-ДУ
=1/ EJ-ДУ


