Постановка задачи. Вычислить объем тела, образованного вращением области, ограниченного графиками функций  и
и  и, возможно, прямыми
и, возможно, прямыми  и
и  , вокруг оси.
, вокруг оси.  План решения
План решения
Объем тела, образованного вращением области, ограниченной кривыми 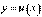 и
и  и прямыми
и прямыми  и
и 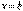 , где
, где  , т.е. области, определяемой системой неравенств
, т.е. области, определяемой системой неравенств  вычисляется по формуле
вычисляется по формуле  . (1)
. (1)
1. Определяем область D. Если неравенства, определяющие область D, неизвестны, т.е. неизвестны a и b и/или неизвестно, какая из функций  и
и  больше другой на отрезке
больше другой на отрезке  , то выполняем следующие операции:
, то выполняем следующие операции:
а) находим a и b как абсциссы точек пересечения графиков функций  и
и  , т.е. решаем уравнение
, т.е. решаем уравнение  ;
;
б) исследуем знак разности  на отрезке
на отрезке  . Для этого достаточно вычислить значение
. Для этого достаточно вычислить значение  в какой-нибудь точке из
в какой-нибудь точке из  . Если оно положительно, то
. Если оно положительно, то  и, следовательно,
и, следовательно,  и
и  . Если оно отрицательно, то
. Если оно отрицательно, то  и, следовательно
и, следовательно  и.
и. 
2. Вычисляем объем по формуле (1).
Замечание 1. Иногда бывает полезным построить график области D и фигуры вращения.
Замечание 2. Аналогично решается задача, если тело образовано вращением области вокруг оси Oy.
Длина дуги пространственной и плоской кривой, заданной параметрически
Если пространственная кривая задана параметрически
 , то длина дуги вычисляется по формуле:
, то длина дуги вычисляется по формуле:

Аналогично для плоской кривой:

Длина дуги плоской кривой, заданной явно
Если функция у = f(x) непрерывно дифференцируема на отрезке [а, b], тогда длина дуги соответствующей кривой имеет вид:

Длина дуги плоской кривой, заданной в полярных координатах
 - непрерывно дифференцируемая на отрезке [
- непрерывно дифференцируемая на отрезке [  ,
,  ] функция, определяющая плоскую кривую;
] функция, определяющая плоскую кривую; 



 . 40.Дифференциальные уравнения. Основные понятия.
. 40.Дифференциальные уравнения. Основные понятия.
Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например,  не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y '(x), y ''(x),..., yn (x) до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функциивремени.
обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
 или
или  ,
,
где 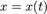 — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени
— неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени  , штрих означает дифференцирование по
, штрих означает дифференцирование по 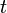 . Число
. Число  называется порядком дифференциального уравнения.
называется порядком дифференциального уравнения.
Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
 ,
,
где  — независимые переменные, а
— независимые переменные, а  — функция этих переменных.
— функция этих переменных.



 и
и  и, возможно, прямыми
и, возможно, прямыми  и
и  , вокруг оси.
, вокруг оси.  План решения
План решения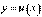 и
и  и прямыми
и прямыми  и
и 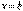 , где
, где  , т.е. области, определяемой системой неравенств
, т.е. области, определяемой системой неравенств  вычисляется по формуле
вычисляется по формуле  . (1)
. (1) и
и  больше другой на отрезке
больше другой на отрезке  , то выполняем следующие операции:
, то выполняем следующие операции: и
и  , т.е. решаем уравнение
, т.е. решаем уравнение  ;
; на отрезке
на отрезке  . Для этого достаточно вычислить значение
. Для этого достаточно вычислить значение  в какой-нибудь точке из
в какой-нибудь точке из  . Если оно положительно, то
. Если оно положительно, то  и, следовательно,
и, следовательно,  и
и  . Если оно отрицательно, то
. Если оно отрицательно, то  и, следовательно
и, следовательно  и.
и. 
 , то длина дуги вычисляется по формуле:
, то длина дуги вычисляется по формуле:


 - непрерывно дифференцируемая на отрезке [
- непрерывно дифференцируемая на отрезке [  ,
,  ] функция, определяющая плоскую кривую;
] функция, определяющая плоскую кривую; 

 не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных. или
или  ,
,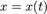 — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени
— неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени  , штрих означает дифференцирование по
, штрих означает дифференцирование по 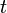 . Число
. Число  называется порядком дифференциального уравнения.
называется порядком дифференциального уравнения. ,
, — независимые переменные, а
— независимые переменные, а  — функция этих переменных.
— функция этих переменных.


