11. Задачи, приводящие к понятию производной (задача о касательной, задача о производительности труда).
Определение. Касательной к данной кривой в данной точке М называется предельное положение МТ секущей ММ1, проходящей через точку М, когда вторая точка пересечения М1 неограниченно приближается по кривой к точке М.
12. Определение производной (приращение функции и приращение аргумента, определение производной функции, геометрический смысл производной, связь между непрерывностью и дифференцируемостью, кусочно-гладкие функции).
13. Схема вычисления производной.
Производная функции у=f(х) может быть найдена по схеме:
1. Дадим аргументу х приращение Dх≠0 и найдем наращенное значение функции у+Dу=f(х+Dх).
2. Находим приращение функции Dу= f(х+Dх)-f(х).
3. Составляем отношение 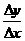 .
.
4. Находим предел этого отношения при 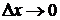 , т.е.
, т.е. 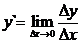 (если этот предел существует).
(если этот предел существует).
Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна
14. Правила дифференцирования. Производная сложной и обратной функций.
Теорема 1. Производная суммы (разности) двух функций:
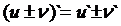 . (1)
. (1)
Теорема справедлива для любого конечного числа слагаемых.
Теорема 2. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
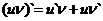
Теорема 3. Производная частного двух функций 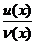 , если
, если 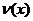 ≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
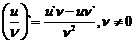 .
.
Теорема 4. Если y = f(u) и и = (ф(х)) — дифференцируемые функции своих аргументов, то производная сложной функции у = f (ф(х)) существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
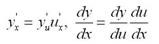
15. Таблица основных производных.
| № п/п
| Функция у
| Производная
| № п/п
| Функция 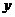
| Производная
|
|
| с
|
|
| 
| 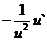
|
|
| х
|
|
| 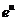
| 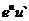
|
|
| 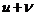
| 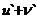
|
| 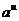
| 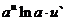
|
|
| 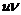
| 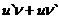
|
| 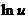
| 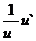
|
|
| 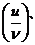
| 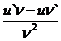
|
| 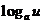
| 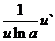
|
|
| 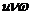
| 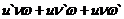
|
| 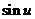
| 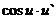
|
|
| 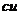
| 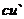
|
| 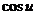
| 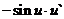
|
|
| 
| 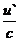
|
| 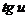
| 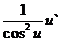 
|
|
| 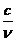
| 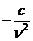
|
| 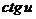
| 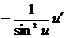
|
|
| 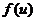 , , 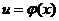
| 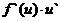
|
| 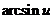
| 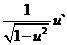
|
|
| 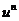
| 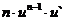
|
| 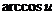
| 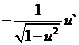
|
|
| 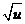
| 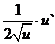
|
| 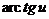
| 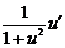
|
|
| 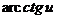
| 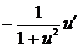
|
| | | | | | | |
16. Производные высших порядков. Дифференциал функции. Понятие дифференциала высшего порядка.
Если функция 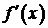 дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается 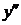 (или
(или 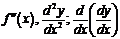 . Итак,
. Итак, 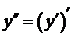 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается 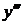 .
.
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
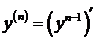 .
.
Дифференциалом функции y=f(x) в точке х называется главная линейная относительно ∆х часть приращения функции, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x)):
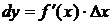 .
.
Дифференциал dy называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т.е. дифференциал функции у = х.
Так как у´=х´=1, то согласно формуле (1), имеем dy=dx=∆x, т.е. дифференциал независимой переменной равен приращению переменной: dx=∆x.
Поэтому формулу можно записать так:
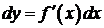 .
.
Иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
17. Применение дифференциала для приближенных вычислений.
18. Основные теоремы дифференциального исчисления (Ферма, Роля, Лагранжа, Коши). Правила Лопиталя.
Теорема Ферма. Если дифференцируемая на промежутке Х функция 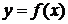 достигает наибольшего или наименьшего значения во внутренней точке
достигает наибольшего или наименьшего значения во внутренней точке 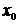 этого аргумента, то производная функции в этой точке равна нулю, т.е.
этого аргумента, то производная функции в этой точке равна нулю, т.е. 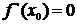 .
.
Геометрический смысл теоремы Ферма очевиден: в точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к графику функции параллельна оси абсцисс.
Теорема Роля. Пусть функция 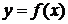 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке 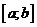 ;
;
2) дифференцируема на интервале 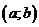 ;
;
3) на концах отрезка принимает равные значения, т.е. 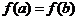 .
.
Теорема Лагранжа. Пусть функция 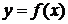 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке 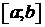 ,
,
2) дифференцируема на 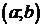 .
.
Теорема Коши. Если функции f(x) и g(x):
1) непрерывны на отрезке 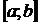 ;
;
2) дифференцируемы в интервале 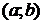 , g(a)≠g(b) и g´(x)≠0 для всех
, g(a)≠g(b) и g´(x)≠0 для всех 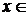
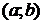
то существует точка с 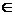
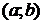 такая, что
такая, что
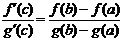 .
.
Теорема (правило Лопиталя раскрытия неопределенности 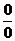 ).
).
Коротко полученную формулу читают так: предел отношения двух бесконечно малых функций равен пределу отношения их производных, если последний существует.
19. Интервалы выпуклости и точки перегиба (определение выпуклости вверх и выпуклости вниз, схема исследования функции на выпуклость).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции объединяются общим названием экстремума функции.
Теорема (необходимое условие экстремума). Если дифференцируемая функция 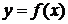 имеет экстремум в точке
имеет экстремум в точке 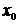 , то ее производная в этой точке равна нулю
, то ее производная в этой точке равна нулю 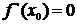 .
.
Непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими (или стационарными). Эти точки должны входить в область определения функции.
Теорема (первое достаточное условие экстремума). Если непрерывная функция 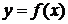 дифференцируема в некоторой окрестности критической точки
дифференцируема в некоторой окрестности критической точки 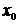 и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 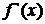 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то 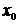 есть точка максимума; с минуса на плюс, то
есть точка максимума; с минуса на плюс, то 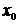 - точка минимума.
- точка минимума.
Схема исследования функции 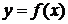 на экстремум.
на экстремум.
1. Найти производную 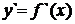 .
.
2. Найти критические точки 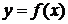 .
.
3. Выбрать из них лишь те, которые являются внутренними точками области определения функции.
4. Исследовать знак производной 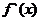 слева и справа от каждой из выбранных критических точек и сделать вывод о наличии экстремумов функции.
слева и справа от каждой из выбранных критических точек и сделать вывод о наличии экстремумов функции.
5. Найти экстремумы (экстремальные значения) функции.
Теорема (второе достаточное условие экстремума). Если в точке 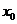 первая производная функции
первая производная функции 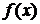 равна нулю (
равна нулю (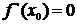 ), а вторая производная в точке
), а вторая производная в точке 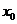 существует и отлична от нуля (
существует и отлична от нуля (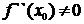 ), то при
), то при 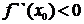 в точке
в точке 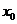 функция имеет максимум и минимум - при
функция имеет максимум и минимум - при 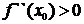 (без доказательства).
(без доказательства).
- 3 -
Определение. График дифференцируемой функции 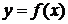 называется выпуклым вниз на интервале
называется выпуклым вниз на интервале 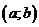 , если он расположен выше любой ее касательной на этом интервале. График функции
, если он расположен выше любой ее касательной на этом интервале. График функции 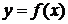 называется выпуклым вверх на интервале
называется выпуклым вверх на интервале 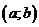 , если он расположен ниже любой ее касательной на этом интервале.
, если он расположен ниже любой ее касательной на этом интервале.
Определение. Точка графика непрерывной функции 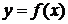 , отделяющая его части разной выпуклости, называется точкой перегиба.
, отделяющая его части разной выпуклости, называется точкой перегиба.
20. Асимптоты графика функции (определение, основные виды, способы нахождения).
Определение. Асимптотой графика функции 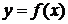 называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки 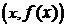 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Определение. Прямая 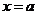 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 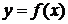 , если
, если 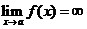 , или
, или 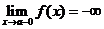 , или
, или 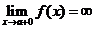 .
.
Определение. Прямая 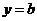 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 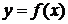 при
при 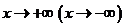 , если
, если  .
.
21. Интервалы монотонности и точки экстремума (основные определения, необходимые и достаточные условия существования экстремума).
22. Схема исследования графика функции.
При исследовании функций и построения их графиков рекомендуется использовать следующую схему.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3. Выяснить, является ли функция четной, нечетной или общего вида.
4. Найти асимптоты графика функции.
5. Найти интервалы монотонности функции.
6. Найти экстремумы функции.
7. Найти интервалы выпуклости и точки перегиба графика функции.
8. На основании проведенного исследования построить график функции.
Если всех пунктов не достаточно, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции.



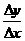 .
.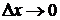 , т.е.
, т.е. 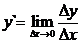 (если этот предел существует).
(если этот предел существует).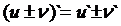 . (1)
. (1)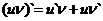
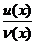 , если
, если 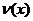 ≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.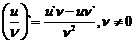 .
.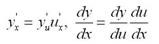
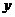

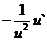
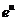
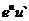
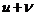
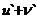
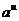
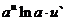
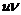
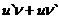
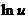
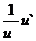
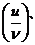
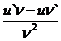
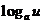
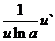
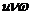
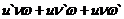
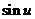
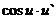
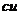
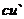
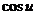
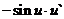

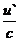
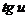
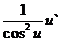

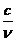
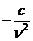
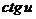
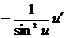
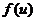 ,
, 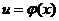
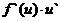
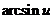
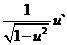
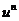
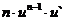
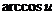
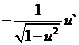
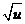
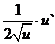
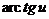
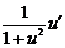
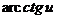
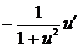
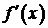 дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается 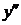 (или
(или 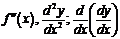 . Итак,
. Итак, 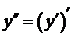 .
.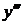 .
.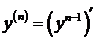 .
.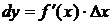 .
.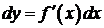 .
.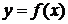 достигает наибольшего или наименьшего значения во внутренней точке
достигает наибольшего или наименьшего значения во внутренней точке 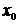 этого аргумента, то производная функции в этой точке равна нулю, т.е.
этого аргумента, то производная функции в этой точке равна нулю, т.е. 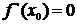 .
.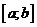 ;
;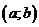 ;
;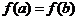 .
.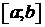 ,
,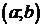 .
.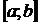 ;
;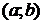 , g(a)≠g(b) и g´(x)≠0 для всех
, g(a)≠g(b) и g´(x)≠0 для всех 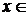
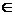
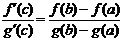 .
.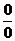 ).
).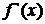 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то 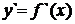 .
.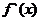 слева и справа от каждой из выбранных критических точек и сделать вывод о наличии экстремумов функции.
слева и справа от каждой из выбранных критических точек и сделать вывод о наличии экстремумов функции.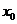 первая производная функции
первая производная функции 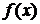 равна нулю (
равна нулю (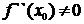 ), то при
), то при 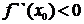 в точке
в точке 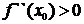 (без доказательства).
(без доказательства).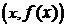 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.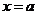 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 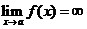 , или
, или 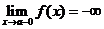 , или
, или 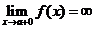 .
.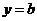 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 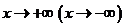 , если
, если  .
.


