Э.Н.Гордеев
ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
Учебное пособие
по дисциплине «Теория информации».
Москва
(С) 2016 МГТУ им. Н.Э. БАУМАНА
УДК 519.7
Гордеев Э.Н.
Основы теории информации. - М.: МГТУ имени Н.Э. Баумана, 2016. 123 с.
Издание содержит конспект лекций по курсу «Основы теории информации», предусмотренного учебным планом МГТУ им. Н.Э.Баумана для студентов инженерных специальностей. Представлены результаты классической теории информации, относящиеся к представлению информации, сжатию информации и защите информации от помех при ее передаче.
Для студентов инженерных специальностей факультета «Информатики и систем управления» МГТУ имени Н.Э. Баумана.
Рекомендовано учебно-методической комиссией НУК «Информатики и систем управления» МГТУ им. Н.Э. Баумана
© 2016 МГТУ имени Н.Э. Баумана
Оглавление
Введение. 7
Раздел 1. Информация и Алгоритм. Коды объектов. 10
1 Информация и алгоритм. 10
1.1 Задачи, алгоритмы.. 10
1.1.1 Задача. 10
1.1.2 Алгоритм. 13
2 Представление (кодирование) информации. 16
2.1.1 Примеры кодировок. 19
2.1.2 Свойства кодировок. 21
2.2 Способы представления (кодирования) информации. 23
2.2.1 Кодирование слов и поиск минимального кода. 23
2.2.2 Признаковое кодирование. 25
Раздел 2. Сжатие информации. 29
3 Кодирование информации. Количество информации. Сжатие информации. 29
3.1.1 Сериальное кодирование. 29
3.1.2 Алфавитное кодирование. 31
3.1.3 Кодирование натурального ряда. 36
4 Количество информации. Энтропия. 40
4.1.1 Энтропия по Хартли. 40
4.1.2 Энтропия по Шеннону. 40
5 Теорема Шеннона. 43
6 Алгоритмы кодирования. 45
6.1 Алгоритм Шеннона (Фано). 45
6.2 Алгоритм Хаффмана. 47
6.3 Блочное кодирование Хаффмена. 49
6.4 Алгоритм арифметического кодирования. 51
7 Блочное кодирование и теорема Шеннона. 53
Раздел 3. Передача информации. Защита от искажений. 55
8 Передача информации по каналу с шумом. 55
8.1 Модели каналов. 56
8.2 Необходимые определения. 59
8.2.1 Пример кода для канала с выпадением. 60
8.3 Передача информации по двоичному симметричному каналу с шумом 62
8.3.1 Схема и принципы кодирования. 62
8.3.2 Принципы построения кодов, исправляющих ошибки. 62
8.3.3 Декодирование на основе таблицы декодирования. 66
8.3.4 Схема кодирования по принципу наибольшего правдоподобия на основе принципа избыточности. 69
8.4 Корректирующие способности кодов. Границы мощности. 71
8.5 Теорема Шеннона для канала с шумом. 78
8.5.1 Факты из теории вероятности. 78
8.5.2 Схема кодирования и декодирования. Вспомогательные утверждения. 79
8.5.3 Вторая теорема Шеннона. 84
8.5.4 Комбинаторное доказательство теоремы. 86
9 Примеры кодов, исправляющих ошибки. Линейные коды. 92
9.1 Линейные коды. 92
9.1.1 Спектр кода. 97
9.2 Код Хэмминга. 99
9.3 БЧХ – коды.. 104
10 Вопросы для самопроверки. 111
11 Примеры билетов для контрольных работ. 113
11.1 КР №1. 113
11.2 КР №2. 115
11.3 КР №3. 116
Приложение. 118
12 Рекомендованная литература. 122
Предисловие.
Предмет курса
Данный текст представляет собой курс лекций, посвященный математическим моделям и методам, используемым при передаче, приеме и хранении информации. В нем отражены основные классические результаты Теории информации, а также некоторые результаты последних десятилетий, которые могут быть отнесены к теории информации.
Основная цель курса
Цель курса - научить студентов ориентироваться в классической теории информации, а также дать представление о тех разделах математики и информатики, которые используются для построения математических моделей задач теории информации.
Это даст возможность будущему специалисту понимать, для каких задач вообще нужна математика, а там, где она нужна, привлекать для работы необходимые определения, понятия и результаты.
Курс лекций предназначен для студентов 3-4 курса. Это именно лекции, а не систематизированный учебник. Автор пытался сохранить в тексте комментарии и пояснения, быть может, не свойственные строгому математическому пособию. Некоторые из них выглядят простыми и очевидными, однако преподавательский опыт показывает, что они полезны для лучшего усвоения материала.
Предполагается, что студент знаком с некоторым базовым набором математических объектов и результатов, что он прослушал хотя бы семестровые курсы по комбинаторике, дискретной математике, теории вероятностей, линейной алгебре, общей алгебре. Курс предшествует таким дисциплинам как: теория массового обслуживания, теория кодирования, теория сложности алгоритмов. Предполагается, что знакомство с данным курсом поможет студентам быстрее и легче освоить эти дисциплины.
Курс состоит из трех разделов. Так как уровень студентов со временем меняется и большинство из них ждет инженерное будущее, то это скорее курс именно для инженеров, а не для математиков, поэтому автор на практике сопровождает лекции большим количеством примеров. В текст включено, как правило, только по одному примеру каждого типа.
Введение.
Теория информации и смежные дисциплины.
Каково место теории информации среди других областей науки? Чтобы ответить на этот вопрос, заметим, что научная дисциплина, имеющая определенное название, определяется объектом и методологией исследования.
Объектом исследования теории информации является информация. Считается, что это «интуитивно очевидное» понятие. Однако в математической дисциплине оперировать интуитивно очевидными понятиями нельзя, хотя и приходится. К подобным понятиям относятся, например: единица, число, множество, алгоритм и т.п. Понятие информации из этого же разряда.
Насегодня неизвестно, что это такое. Фраза: «Информация – нематериальная сущность, не имеющая физических атрибутов» - ничего не определяет. Ниже мы попытаемся как-то прояснить это понятие, но до формального определения, конечно, не дойдем.
Информация, как объект исследования, фигурирует во многих дисциплинах: информатике, кибернетике, криптографии, теории связи и др. При описании взаимоотношения различных дисциплин надо делать скидку на условности и точку зрения описывающего, поэтому подобные описания варьируются в зависимости от автора.
В целом же, Информатика, Кибернетика и Теория информации – различные науки, а значит должны отличаться либо объектами, либо методологией.
Кибернетика – наука о:
1. Получении информации;
2. Хранении информации;
3. Передачи информации;
4. Преобразовании информации;
5. Использовании информации.
Такое же определение можно дать и двум другим упомянутым дисциплинам. Ключевым словом для кибернетики является «управление». Объектом исследования являются живые и неживые материальные системы. Кибернетика при этом определяется как наука о том, что и как позволяет управлять этими системами. При этом слово «управление», указывает на то, что появляется процесс, с помощью которого в управляемой системе происходит изменение и который передает некую информацию, на основе которой в системе и происходит изменение. Это изменение может, например, привести к существенным энергетическим обменам между системой и средой. В то же время процесс управления, как правило, требует сравнительно малой энергии и использует то, что называется информацией.
Некоторые авторы считают теорию информации разделом кибернетики. Другимиразделами кибернетики считаются: теория массового обслуживания, теория алгоритмов, теория автоматов, исследование операций, теория оптимального управления и теория распознавания образов.Мы же, в силу специфики курса, будем трактовать область исследования теории информации несколько шире, поэтому вторгнемся в пограничные области упомянутых дисциплин.
В конце 70-х начале 80-х годов в нашей стране появилось понятие «информатика» (англ. “ Computer Science ”). Это тоже наука о получении, хранении и использовании информации, но ее проблематика связана с появлением и развитием компьютеризации. По сути, и в кибернетике и в информатике ставятся одинаковые задачи, но в информатике доминируют постановки задач из области именно компьютерных технологий.
Связисты же считают, что Теория информации хотя сегодня и может рассматриваться частью и кибернетики и информатики, но намного старше их по возрасту. Однако ранее в термин Теория информации вкладывался несколько отличный от сегодняшнего смысл. Теория информации, по мнению связистов, выросла из инженерной дисциплины, разрабатывающей системы связи и сигнализации.
В информатике, кибернетике и теории информации используются многие методы классической математики, но наиболее важны здесь методы теории вероятностей, дискретной математики, алгебры и комбинаторики.
Поводя итог, можно сказать, что Теория информации представляет собой математическую теорию, посвященную исследованию понятия информации и математических методов представления информации, измерению информации, формализации каналов и протоколов передачи информации в различных условиях (с помехами и без них), построению методов защиты информации от помех при передаче, а также вопросам преобразования информации для ее эффективного хранения.
Первоначально теория примерялась к радио, телеграфии, телевидению и к другим средствам связи и была посвящена каналу связи, определяемому длиной волны и частотой, реализация которого была связана с колебаниями воздуха или электромагнитным излучением. Обычно соответствующий процесс был непрерывным, но мог быть и дискретным, когда информация кодировалась, а затем декодировалась.
Информация и алгоритм.
Два интуитивных понятия: информация и алгоритм взамообуславливают друг друга.
Задачи, алгоритмы
В этом Разделе мы будем иметь дело с несколькими лишь интуитивно определяемыми понятиями. Важнейшие из них - задача и алгоритм.
Задача
В общем случае, алгоритм для чего-то субъектам, его использующим, нужен. Он, например, что-то дает им дает или что-то им обеспечивает. То есть, у субъекта есть потребность к достижению (обладанию, пониманию и т.п.) чего-то. Достигается это путем порождения новой сущности или преобразования одной сущности в другую: алгоритм построения дома, поиск кратчайшего пути с работы домой, умножение чисел и т.п.
При этом под алгоритмом понимается не сам процесс, а инструкция по его осуществлению. Такая инструкция, нанесенная на материальный носитель, будет информационным объектом, но такими же информационными объектами будут исходные данные для осуществления алгоритма и результат его работы.Будем считать, что реализация этой потребности достигается решением задачи. У задачи есть исходные данные (условие) и результат. Алгоритм и дает инструкцию по преобразованию их одно в другое.
То же такое задача? При описании базовых понятий или аксиоматики используется три способа: аналогия, пример и расчленение «менее элементарных» сущностей на совокупность «более элементарных». Пойдем и мы по этим путям.
Самая простая идентификация понятия может быть дана по аналогии. Так как у нас математический курс, то проведем аналогию с двумя математическими дисциплинами: математической логикой и дискретной математикой, потому что именно эти дисциплины наибольшее внимание уделяют понятиям алгоритм и задача.
Вспомним то, что имелось в виду под задачей в этих дисциплинах. В нашем курсе мы будем иметь дело примерно с тем же самым.
Например, в [1] определение задачи вообще не дается, считается, что оно «интуитивно очевидно». В [2] под задачей понимается «некоторый общий вопрос, на который следует дать ответ». При этом «задача содержит несколько параметров или свободных переменных, конкретные значения которых не определены».
В [4] под задачей понимается «выбор наилучшей конфигурации или множества параметров для достижения некоторой цели». При этом задачи делятся на непрерывные и комбинаторные. «В непрерывных задачах обычно отыскивается множество действительных чисел или даже некоторая функция; в комбинаторных задачах – некоторый объект из конечного или возможно бесконечного счетного множества». Другими словами, задача оптимизации – это пара (F,c), где F – произвольное множество, область допустимых точек, а c - функция стоимости, отображающая элементы F на множество действительных чисел. Требуется найти такую x* точку из F, на которой значение функции c (x*) обладает определенным свойством, например, минимально, максимально и пр.
Теперь займемся «расчленением» сущностей, приведенных выше. Задачи, рассматриваемые в нашем курсе, это, в подавляющем большинстве, задачи комбинаторные или дискретные. Уже само слово комбинаторный относится к упомянутому выше множеству F. Вернее, к способу его задания. Мы видим, что при таком задании с задачей обычно связывается два объекта: множество параметров и структура связей между ними. Параметры – «язык» для описания условий задачи. Структура связей содержит нечто, позволяющее описать F, а также сформулировать вопрос (см. [2]) или требование к c (x*) трактуемое как вопрос, свойство функционала и пр. (См. [4]).
В теории сложности алгоритмов термин задача сразу же разбивается на два термина: индивидуальная задача и массовая задача. Это связаны со способом задания параметров. Массовая задача предполагает описание множества параметров, а индивидуальная задача возникает, при фиксации значений этих параметров.
Алгоритм
С понятием алгоритма дело обстоит сложнее. Работа в этом направлении породила не только теорию сложности алгоритмов или столь распространенные сейчас компьютеры, но и разделение математики, в которой на некоторое время остро стал вопрос о конструктивности.
Формализация понятия "алгоритм" необходима также из-за "несимметричности" ответа на вопрос, существует ли алгоритм для решения задачи Z?
Действительно, ответ "да" может быть получен путем построения некоторой процедуры решения, которая укладывается в "интуитивное" понятие алгоритма. Такие процедуры и строились в процессе всей истории математики, когда формальным построениям самого понятия алгоритм внимания не уделялось. Если для некоторой задачи не могли построить метода решения, то это списывалось на недостаток умения.
Имея лишь интуитивное представление об алгоритме, нельзя доказать, что этого самого алгоритма не существует.
В 30-е годы стали появляться первые формальные схемы алгоритма. Эти схемы были предназначены исключительно для теоретических исследований. В качестве примеров рассмотрим две из них. Речь пойдет, например, о машинах Тьюринга (МТ), нормальных алгорифмах Маркова (НАМ) и др.
Алгоритм производит некоторые "действия" с объектами и параметрами, начиная с исходных условий задачи (входные условия, вход). Во всех известных формальных схемах этот вход как-то задается. В самом общем случае можно считать, что это задание выглядит в виде слова в некотором алфавите.
Если множество символов одного алфавита является подмножеством символов другого, то первый называется подалфавитом второго. А второй - надалфавитом первого.
Пусть A - подалфавит некоторого алфавита B. Слово, состоящее из символов алфавита A, будем называть словом в алфавите A. Слово, состоящее из символов алфавита B, будем называть словом над алфавитом A.
Заметим, что достаточно ограничиться алфавитом из двух символов, например, 0 и 1. Любой символ ai алфавита A={a1,…,an,…} может быть закодирован следующим образом: ai =011...10, где 1 повторяется n раз.
В известных формальных схемах (формализмах) "алгоритм" можно представить как некоторое пошаговое преобразование одних слова в другие, начиная с входа x1,…,xn = X. В результате последнего шага таких преобразований получаем некоторое выходное слово Y. Его можно трактовать как результат работы алгоритма. Задавая буквы входного алфавита числовыми последовательностями, можно считать, что речь идет о вычислении функции f(x1,…,xn)=f(X)=Y.
Обратим внимание на употребление понятия эквивалентности в связи с наличием нескольких возможных представлений (кодировок, способов записи) входных объектов.
Два выражения (кодировки) B и C считаются эквивалентными B»C в двух случаях: либо оба выражения не определены (бессмысленны), либо определены и обозначают один и тот же объект.
Будем говорить, что алгоритм Á является алгоритмом в алфавите A, если он переводит слова x1,…,xn в алфавите A в слова f(x1,…,xn) в алфавите A.
Будем говорить, что алгоритм Á является алгоритмом над алфавитом A, если он переводит слова x1,…,xn над алфавитом A в слова f(x1,…,xn) над алфавитом A.
При этом алгоритмÁ может работать не с любыми словами алфавита. Множество тех слов, к которым он применим, назовем областью действия алгоритма Á, а результат применения алгоритма Á к слову P обозначим через Á (P). При этом сам алгоритм не обязан распознавать слова из своей области действия.
Рассмотрим два алгоритма Á и Â над алфавитом A.
Если Á(P)»Â(P) для любого слова P в алфавите A, то эти алгоритмы называются вполне эквивалентными относительно A.
Если Á(P)»Â(P) для любого слова P в алфавите A такого, что хотя бы одно из выражений Á(P) или Â(P) определено и является словом в алфавите A, то эти алгоритмы называются эквивалентными относительно A.
Рассматриваемые ниже формальные подходы к понятию алгоритма заслужили внимание благодаря гипотезам типа тезиса Черча.
Этот тезис говорит об эквивалентности широкого неформально и смутного понятия "интуитивный алгоритм" узкому и весьма замысловатому, на первый взгляд, формализму типа алгорифма Маркова (МТ) или машины Тьюринга. Утверждается, что для любой задачи, для которой существует «интуитивный» алгоритм решения, можно, например, построить МТ, которая будет решать эту задачу.
Сделаем одно замечание. Во всех перечисленных ниже формальных подходах алгоритм имеет дело с преобразованием одних слов в другие. То есть, условие задачи Z можно рассматривать как слово в некотором алфавите A.
Обозначим все множество слов этого алфавита через A*. Подмножество слов алфавита назовем языком. Обратим внимание, что в содержательном смысле не все слова алфавита являются условиями индивидуальных задач из Z.
После проведенного рассмотрения очевидно, что алгоритма без информации не существует. Если мы хотим дать определение алгоритма, нам нужно определение информации.
Во избежание выхода в область философии и ненужных споров ограничимся областью точных наук, а также инженерии и производства. Тогда мы утверждаем, что справедливо и обратное: информации без алгоритма не существует.
Исходные данные для задачи - это код (представление информации)некоторого объекта. Вид же кода и требования к нему зависят от задачи, в которой этот код будет использоваться. Этому мы и посвятим следующий раздел.
Примеры кодировок
Приведем простые примеры кодирования объектов.
Целые числа
Целое число n может быть представлено (закодировано), например, следующими тремя способами.
а) Словом α = 01…10 (n штук «1» и 0 по бокам) в алфавите А=(0,1). В этом случае длина кода l(α) (количество символов алфавита в слове) равна n+2;
б) Словом α = a 1 a 2 …ak в виде десятичной записи в алфавите А=(0,1,…,9). Длина кода равна[lg n ]+1.
в) В мультипликативной форме (произведение степеней простых множителей) в виде слова α = a 1 p 1 a 2 p 2 …akpk, (здесь a 1 … ak – простые числа).
Длина кода:  .
.
Вектора и матрицы
Вектор с компонентами a 1 … an, записанными в десятичной форме имеет, может быть представлен в виде слова длиныlg n +  .
.
Матрица Mс компонентами в десятичной форме, M= 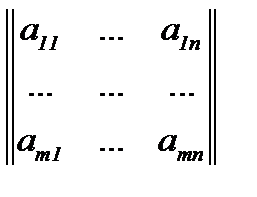 ,может быть представлена словом длиныlg n + lg m +
,может быть представлена словом длиныlg n + lg m +  .
.
G = ( V, E ) – неориентированный граф.
Здесь множество вершин обозначено черезV, а множество ребер черезE. Пусть |V| = n, |E| = m.
Граф можно представить, например, следующими тремя способами (все числа в десятичной форме)
а) Списком ребер {(i 1, j 1), (i 2, j 2), …, (im, jm)}.
б) Списком соседей (вершин), записанных последовательно для вершины 1, вершины 2,…, вершины n.

в) Матрицей смежности
A = | aij |n×n, 


 .
.
Алфавит А кроме арабских цифр будет включать вспомогательные разделители, например, «,» и «;».
Длина кодаl(α) без учета разделителей для каждого из трех случаев следующая:
а) 4n + 1 0m ≤ l(α) ≤4n + 1 0m + (n+ 2 n).
б) 2 n + 8m ≤ l(α) ≤ 2 n + 8m + 2log n.
в) l(α) = n 2 – n – 1.
Пример.
1. (1 2), (1 4), (1 5), (2 3), (3 4), (2 4), (5 3)
2. (2 4 5), (3 4), (4 5)
3. 
Свойства кодировок
К коду β объекта α обычно применяют следующие требования.
Декодируемость. В случае кодирования (как преобразования слов) это свойство не вызывает вопросов. Пусть есть объект α, код β= φ(α). Декодируемость означает умение восстанавливать α по коду β= φ(α). В случае же кодирования в широком аспекте словом является только β. Сам объект α словом не является. Поэтому в каждом конкретном случае нужно определять понятие восстановление. В качестве примера можно привести пример присвоения идентификатора (слово в алфавите) неформализованному объекту (изделие, книга, человек). Здесь под восстановлением понимается нахождение конкретного объекта по его идентификатору.
Неизбыточность. Это требование означает стремление уменьшить длину кода. Но пока речь не идет об оптимизации и минимизации. Неизбыточность в широком смысле означает не поиск минимально возможной (по длине кода) кодировки, а использование известной кодировки без искусственного увеличения ее длины.
Разумность. Это термин из теории сложности алгоритмов. Он означает, что способ кодировки должен соответствовать тем целям, для которых информация будет использоваться в дальнейшем. Например, если мы решаем задачу о простоте числа (по заданному натуральному числу N требуется ответить на вопрос, является ли это число простым), то кодировка в мультипликативной форме (см. пример выше) не является разумной. Для большинства практических задач кодировка а) числа nв Примере а)для кодирования целых чисел не является разумной.
Пусть мы теперь имеем "разумные" кодировки. На этом уровне принимается интуитивная гипотеза о некоторой эквивалентности всех возможных "разумных" кодировок входных данных одной и той же массовой задачи.
Второй пример показывает варианты длины кодировок в зависимости от способа задания чисел. Варианты длины кодировок в третьем примере зависят уже от структуры входных данных. Но в обоих случаях можно говорить о, так называемой, полиномиальной эквивалентности.
В дальнейшем нам полезно будет понятие полиномиальной эквивалентности двух функций. Две неотрицательные функции S(n) и R(n) полиномиально эквивалентны, если существуют два полинома Q(x) и P(x) такие, что для всех n справедливы неравенства S(n)£P(R(n)) и R(n)£Q(S(n)).
Пусть S и R две "разумные" схемы кодирования задачи массовой Z. Длины входа в этих схемах для задачи I обозначим через S(I) и R(I). К ним можно применить определение полиномиальной эквивалентности.
В примере кодирования графа все три схемы полиномиально эквивалентны.
Признаковое кодирование.
Этот метод можно использовать в разных ситуация, но типичное его применение – кодирование неформализованных объектов.
Признаки:
Рассматривается множество объектовs1,…,sm (люди, болезни, месторождения и т.п.), которое нужно кодировать, т.е. каждому объекту нужно сопоставить слово в алфавите. При этом есть другое множество объектов, называемых признаками, которые мы умеем кодировать. Тогда кодом объекта при признаковом кодировании является вектор, компонентами которого являются коды (значения) признаков, применительно к данному объекту.
При признаковом кодировании объекта  признаком называется отображение
признаком называется отображение  , где Df— множество допустимых значений признака. Если заданы признакиf1,…,fn, то вектор x=(f1(x),…,fn(x)) называется признаковым описанием объекта x. Если признаковые описания отождествляют с самими объектами, то множество
, где Df— множество допустимых значений признака. Если заданы признакиf1,…,fn, то вектор x=(f1(x),…,fn(x)) называется признаковым описанием объекта x. Если признаковые описания отождествляют с самими объектами, то множество  называют признаковым пространством.
называют признаковым пространством.
В зависимости от множества признаки делятся на следующие типы:
1. бинарный признак: Df=(0,1);
2. номинальный признак: Df- конечное множество;
3. порядковый признак: Df - конечное упорядоченное множество;
4. количественный признак: Df - множество действительных чисел.
Можно использовать характеристические вектора признаков, например,
α (si) = (α 1, …, αk)  .
.
Пример. s 1 … sn – люди.
Признаки:
1. Цвет волос
2. Рост
- Вес
- p 4 … pn – размеры частей тела человека.
В случае бинарных значений признаков или использовании характеристических векторов при признаковом кодировании объектом исследования является матрица векторов признаков.

Опр. Тест - это множество столбцов в T (A) такое, что все строки в подматрице, образованной этим множеством, попарно различны.
Выше мы уже говорили о стремлении строить неизбыточные коды. С этой задачей связана известная проблема дискретной математики – проблема поиска минимальных тестов таблицы.
Длина теста – количество столбцов в тесте.
Тест будет тупиковым, если никакое его подмножество уже не будет тестом.
Минимальный тест – тест с минимальным количеством столбцов. Длину минимального теста обозначим через t(A).
Когда таблица T (A) – это признаковая таблица множества объектов (строки таблицы – вектора признаков объектов), то длина теста указывает на количество признаков, которых достаточно для различения объектов. Эти признаки соответствуют стобцам теста. Но будет ли их достаточно, если количество объектов увеличиться? В связи с этим вопросом тестовая тематика возникает и при определении качества выбора множества признаков.
Конечно, как математический объект, тест – это скорее тема таких дисциплин как комбинаторика, дискретная математика, теория распознавания, но, так как он тесно связан с проблемой грамотного представления информации, то это объект и теории информации.
Для получения содержательных результатов в области построения минимальных тестов необходимо накладывать ограничение на вид и структуру векторов признаков. В качестве примеров приведем несколько утверждений, доказательство которых либо очевидно, либо является несложным упражнением.(Обозначение приведены выше. Если не оговорено обратное – основание логарифма равно двум).
Утв. Справедливо неравенство
t(A)≥logm.
Заметим, что данное утверждение тесно связано с приведенным ниже понятием энтропия по Хартли. Оно означает, что если объектам даются битовые идентификаторы, то число бит в таком идентификаторе для различения mобъектов не может быть меньше log m.
Утв. Пусть строки матрицы Т(А) устроены так, что вместе с любой парой строк в матрице есть и строка, равная сумме этой пары по модулю два, тогда в такой матрице любой тупиковый тест будет минимальным и
t(A)=logm.
Данное утверждение станет для вас совершенно очевидным, если заметить, что в данном случае множество строк матрицы – подпространство булева куба.
(Ниже мы вернемся к этому вопросу, когда будем рассматривать, так называемые, линейные коды.)
Утв. Число тупиковых тестов таблицы не превосходит  .
.
Утв. Если строками матрицы являются все наборы с четным числом единиц, то число тупиковых тестов такой таблицы равно числу ее столбцов.
Утв. Если строками матрицы являются все наборы с фиксированным числом единиц, то число тупиковых тестов такой таблицы равно числу ее столбцов.
Сериальное кодирование
Здесь А = (0,1) иB = (0,1,…,9,*). Символ * играет роль разделителя.
В данном примере битовые последовательности кодируются натуральными числами. Как это следует из свойств данного кодирование, оно дает эффект сжатия, когда битовые последовательности представляют собой чередование сравнительно больших блоков нулей и единиц.
Алгоритм кодирования. Пусть дана битовая последовательность α и а  (0,1) ее первый символ. Блоком назовем часть последовательности, состоящую из одинаковых символов. Тогда любую битовую последовательность можно представить как чередование блоков из нулей и единиц. Пусть в последовательности α всегоS блоков, длина первого x1, длина второго - x2,…, длинаS –го -xS.Тогда кодом α будет слово β=φ(α)=а*x1*x2*…*xS.
(0,1) ее первый символ. Блоком назовем часть последовательности, состоящую из одинаковых символов. Тогда любую битовую последовательность можно представить как чередование блоков из нулей и единиц. Пусть в последовательности α всегоS блоков, длина первого x1, длина второго - x2,…, длинаS –го -xS.Тогда кодом α будет слово β=φ(α)=а*x1*x2*…*xS.
Алгоритм декодирования очевиден.
Определение. Длиной сериального кода назовем число  где [ log x]*=1 при x=1 и [ log x] при x>1.
где [ log x]*=1 при x=1 и [ log x] при x>1.
Определение. Средней длиной кода для n-последовательностей назовем число
 ,
,
Где сумма берется по всем двоичным последовательностям длины n.
Свойства такого кодирования иллюстрируются следующими двумя утверждениями.
Утверждение. Если все xi=1, то l(α)=|α|.
Утверждение. Если все xi>1, то  .
.
Доказательство.
 .
.
Из этих утверждений следует.

Таким образом, сериальное кодирование при малых количествах серий и большой длине серий приводит к тому, что при таком кодировании возникает эффект сжатия.
Если серии короткие и их много, например:  и
и  , то эффекта сжатия не возникает.
, то эффекта сжатия не возникает.
Для полноты картины приведем два утверждения, доказанные в [7].
Утв. Средняя длина слова с S сериями в сериальном кодировании
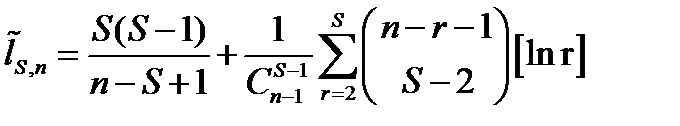 .
.
Утв. Справедлива асимптотическая оценка
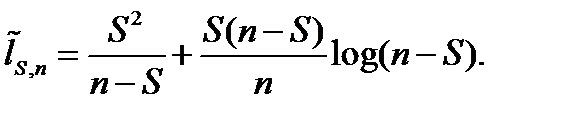
Алфавитное кодирование.
Если пренебречь разделителями, то в качестве двух алфавитов возьмем алфавиты
А = (а 1, …, аn) иB = (b 1, …, bq).
Алгоритм кодирования. Каждой букве ai алфавита A ставится в соответствие Bi=φ(ai) – словов алфавите Bдлины li.
Алфавитное кодирование будет дешифруемым, если отображение 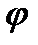 таково, что для
таково, что для  .
.
Заметим, что в приведенном определении термин дешифруемость используется в другом смысле, нежели выше при описании основных свойств кодирования (дешифруемость – неизбыточность-разумность). Поэтому в других учебниках по теории информации используются иные термины, например, разделимость.
Обратим внимание на следующий важнейший факт, который, по сути дела, и оправдывает интерес к такому виду кодирования. Очевидно, что ограничение на вид отображения φ сразу влечет дешифруемость однобуквенных (в алфавите А) слов. Но из дешифруемости однобуквенных слов сразу следует дешифруемость слов (в алфавитеA) любой длины.
Заметим также, что в случае дешифруемого кодирования все слова Bi=φ(ai) обязательно различны.
Оказывается, что дешифруемость накладывает ограничение на набор длин кодовых слов. Об этом говорит утверждение, известное как неравенство Крафта.
Неравенство Крафта.
Теорема. Если алфавитное кодирование с длиной кодов l 1, …, ln дешифруемо, то выполняется неравенство:

Доказательство. Пусть А = (а 1, …, аn) иB = (b 1, …, bq). Каждой букве ai алфавита A ставится в соответствие Bi=φ(ai) – словов алфавите Bдлины li. Положим

Пусть  . ВозведемZ в некоторую степень m, тогда
. ВозведемZ в некоторую степень m, тогда
 .
.
Здесь введено обозначение S (n, t) – числословдлиныtивида Bi 1 Bi 2 …Bin. Из дешифруемости следует, что все такие слова различны, но число различных слов длины tв алфавите из qбукв не превосходит qt, поэтому
S (n, t)  qt.
qt.
Тогда  , где m – натуральное, а l ≥ 0, целое. Это неравенство должно выполняться для любого m, но это возможно только тогда, когда Z не превосходит единицы, т.е.
, где m – натуральное, а l ≥ 0, целое. Это неравенство должно выполняться для любого m, но это возможно только тогда, когда Z не превосходит единицы, т.е.
 .
.
Утверждение доказано.
Префиксные коды.
Опр. Слово α является подсловом слова β, если существуют слова γ и δ (возможно пустые) такие, что β=γαδ.
В общем случае из неравенства Крафта не следует дешифруемость.
Опр. Кодирование называется префиксным, если ни одно из кодовых слов не является началом другого.
Теорема. Префиксный код дешифруем.
Доказательство: Пусть есть α и β – два слова: 
Покажем, что из равенст



 .
. .
. ,может быть представлена словом длиныlg n + lg m +
,может быть представлена словом длиныlg n + lg m +  .
.


 .
.
 признаком называется отображение
признаком называется отображение  , где Df— множество допустимых значений признака. Если заданы признакиf1,…,fn, то вектор x=(f1(x),…,fn(x)) называется признаковым описанием объекта x. Если признаковые описания отождествляют с самими объектами, то множество
, где Df— множество допустимых значений признака. Если заданы признакиf1,…,fn, то вектор x=(f1(x),…,fn(x)) называется признаковым описанием объекта x. Если признаковые описания отождествляют с самими объектами, то множество  называют признаковым пространством.
называют признаковым пространством. .
.
 .
. (0,1) ее первый символ. Блоком назовем часть последовательности, состоящую из одинаковых символов. Тогда любую битовую последовательность можно представить как чередование блоков из нулей и единиц. Пусть в последовательности α всегоS блоков, длина первого x1, длина второго - x2,…, длинаS –го -xS.Тогда кодом α будет слово β=φ(α)=а*x1*x2*…*xS.
(0,1) ее первый символ. Блоком назовем часть последовательности, состоящую из одинаковых символов. Тогда любую битовую последовательность можно представить как чередование блоков из нулей и единиц. Пусть в последовательности α всегоS блоков, длина первого x1, длина второго - x2,…, длинаS –го -xS.Тогда кодом α будет слово β=φ(α)=а*x1*x2*…*xS. где [ log x]*=1 при x=1 и [ log x] при x>1.
где [ log x]*=1 при x=1 и [ log x] при x>1. ,
, .
. .
.
 и
и  , то эффекта сжатия не возникает.
, то эффекта сжатия не возникает.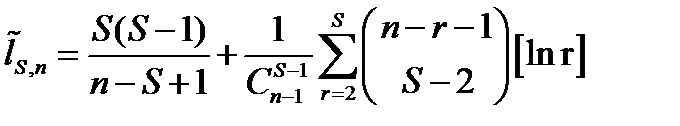 .
.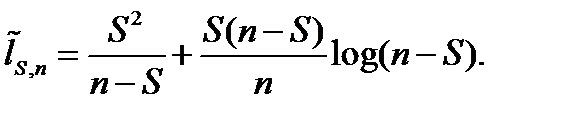
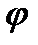 таково, что для
таково, что для  .
.





 . ВозведемZ в некоторую степень m, тогда
. ВозведемZ в некоторую степень m, тогда .
. qt.
qt. , где m – натуральное, а l ≥ 0, целое. Это неравенство должно выполняться для любого m, но это возможно только тогда, когда Z не превосходит единицы, т.е.
, где m – натуральное, а l ≥ 0, целое. Это неравенство должно выполняться для любого m, но это возможно только тогда, когда Z не превосходит единицы, т.е. .
.



