Длина кривой
Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором 
. Длина данной кривой выражается следующим криволинейным интегралом

где  − производная, а
− производная, а 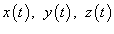 − компоненты векторной функции
− компоненты векторной функции 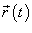 .
.
Наконец, если кривая C задана в полярных координатах уравнением 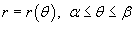 ,
,
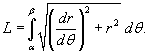
Площадь области, ограниченной замкнутой кривой
Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости O xy Тогда площадь области R, ограниченной данной кривой, определяется формулами
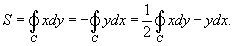
Если замкнутая кривая C задана в параметрическом виде  , то площадь соответствуюшей области равна
, то площадь соответствуюшей области равна
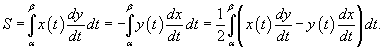
Объем тела, образованного вращением замкнутой кривой относительно оси Ox
Предположим, что область R расположена в верхней полуплоскости y ≥ 0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки. В результате вращения области R вокруг оси O x образуется тело Ω (рисунок 2). Объем данного тела определяется формулами
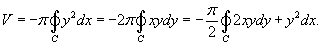
Криволинейные интегралы 2 рода
Предположим, что кривая C задана векторной функцией 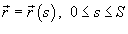 , где переменная s − длина дуги кривой. Тогда производная векторной функции
, где переменная s − длина дуги кривой. Тогда производная векторной функции
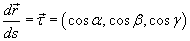
представляет собой единичный вектор, направленный вдоль касательной к данной кривой
Введем векторную функцию 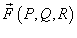 , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции
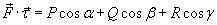
существовал криволинейный интеграл 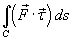 . Такой интеграл
. Такой интеграл 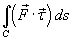 называется криволинейным интегралом второго рода от векторной функции
называется криволинейным интегралом второго рода от векторной функции 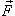 вдоль кривой C и обозначается как
вдоль кривой C и обозначается как
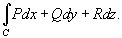
Таким образом, по определению,
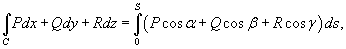
где 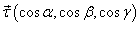 − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
Последнюю формулу можно переписать также в векторной форме:

где 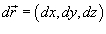 .
.
Если кривая C лежит в плоскости O xy, то полагая R = 0, получаем
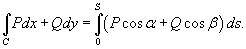
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
1.Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −Cкривую противоположного направления - от B к A. Тогда
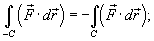
2.Если C − объединение кривых C 1 и C 2 то
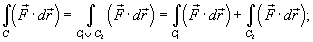
3.Если кривая C задана параметрически в виде 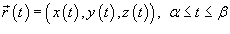 , то
, то
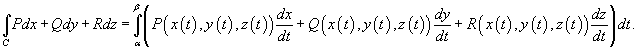
4.Если кривая C лежит в плоскости O xy и задана уравнением 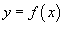 (предполагается, что R = 0и t = x), то последняя формула записывается в виде
(предполагается, что R = 0и t = x), то последняя формула записывается в виде
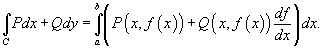
Приложение формулы Грина для выч криволин интегр и площади
Пусть в плоскости O xy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция
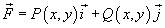
Тогда справедлива формула Грина
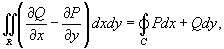
Если 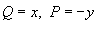 , то формула Грина принимает вид
, то формула Грина принимает вид
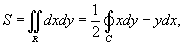
где S − это площадь области R, ограниченной контуром C.
24.Независимость пути интегрирования кринтегр 2 рода
Криволинейный интеграл второго рода от векторной функции  не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция
не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция 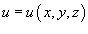 , такая, что
, такая, что
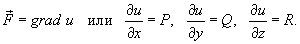
В этом случае криволинейный интеграл второго рода от функции 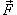 вдоль кривой C от точки A до точки B выражается формулой
вдоль кривой C от точки A до точки B выражается формулой
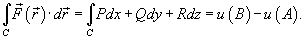
Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
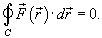
Площадь поверхности
Пусть S является гладкой, кусочно-непрерывной поверхностью. Площадь поверхности определяется интегралом
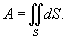
Если поверхность S задана параметрически с помощью вектора
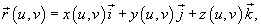
то площадь поверхности будет равна
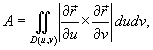
где D (u,v) − это область, в которой задана поверхность.
Если поверхность S задана в явном виде функцией z (x,y), то площадь поверхности выражается формулой
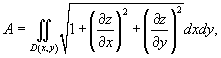
где D (x,y) − проекция поверхности S на плоскость xy.
Масса оболочки
функцией плотности 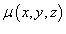 …
… 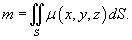
Сила притяжения поверхности
Пусть задана поверхность S, а в точке (x 0, y 0, z 0), не принадлежащей поверхности, находится тело массой m
Сила притяжения между поверхностью S и точечным телом m определяется выражением
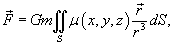
где 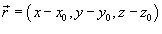 , G - гравитационная постоянная,.
, G - гравитационная постоянная,.
Сила давления
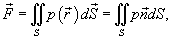
Заряд поверхности
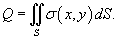
40. Формула Стокса и ее приложение
Пусть S является гладкой поверхностью, ограниченной гладкой кривой C. Тогда для любой непрерывно дифференцируемой векторной функции
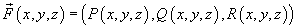
справедлива теорема Стокса:
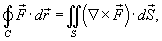
Где − ротор векторного поля 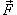 .
.
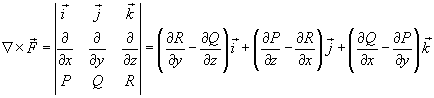
Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова направлена в ту же сторону, что и вектор нормали 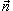 (рисунок 1).
(рисунок 1).
Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.
В координатной форме теорема Стокса может быть записана в следующем виде:

Длина кривой
Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором 
. Длина данной кривой выражается следующим криволинейным интегралом

где  − производная, а
− производная, а 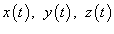 − компоненты векторной функции
− компоненты векторной функции 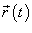 .
.
Наконец, если кривая C задана в полярных координатах уравнением 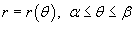 ,
,
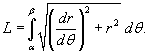
Площадь области, ограниченной замкнутой кривой
Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости O xy Тогда площадь области R, ограниченной данной кривой, определяется формулами
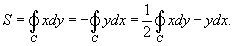
Если замкнутая кривая C задана в параметрическом виде  , то площадь соответствуюшей области равна
, то площадь соответствуюшей области равна
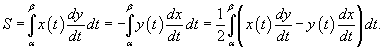





 − производная, а
− производная, а 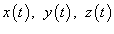 − компоненты векторной функции
− компоненты векторной функции 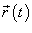 .
.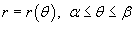 ,
,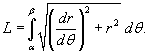
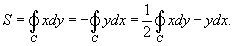
 , то площадь соответствуюшей области равна
, то площадь соответствуюшей области равна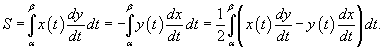
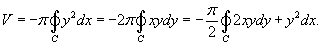
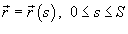 , где переменная s − длина дуги кривой. Тогда производная векторной функции
, где переменная s − длина дуги кривой. Тогда производная векторной функции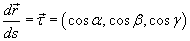
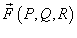 , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции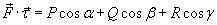
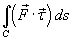 . Такой интеграл
. Такой интеграл 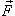 вдоль кривой C и обозначается как
вдоль кривой C и обозначается как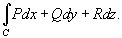
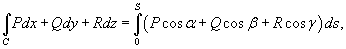
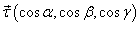 − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
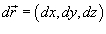 .
.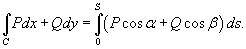
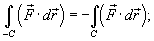
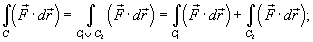
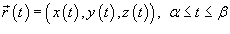 , то
, то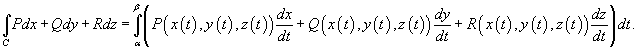
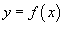 (предполагается, что R = 0и t = x), то последняя формула записывается в виде
(предполагается, что R = 0и t = x), то последняя формула записывается в виде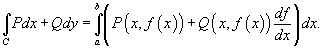
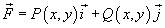
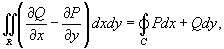
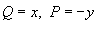 , то формула Грина принимает вид
, то формула Грина принимает вид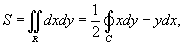
 не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция
не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция 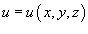 , такая, что
, такая, что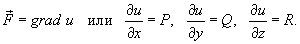
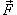 вдоль кривой C от точки A до точки B выражается формулой
вдоль кривой C от точки A до точки B выражается формулой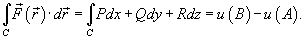
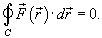
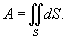
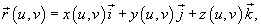
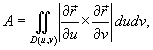
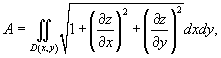
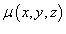 …
… 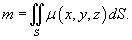
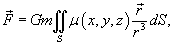
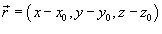 , G - гравитационная постоянная,.
, G - гравитационная постоянная,.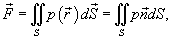
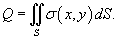
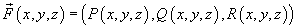
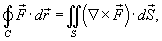
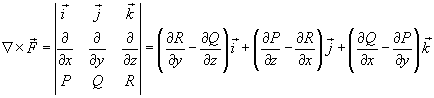
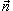 (рисунок 1).
(рисунок 1).


