По правилу суммы, мощность объединения двух не пересекающихся множеств равна сумме их мощностей. В общем же случае, когда множества A и B могут пересекаться, в сумме  некоторые элементы из множества
некоторые элементы из множества  сосчитаны дважды. Это те элементы, которые принадлежат пересечению
сосчитаны дважды. Это те элементы, которые принадлежат пересечению  . Следовательно, мощность объединения двух конечных множеств можно найти по формуле:
. Следовательно, мощность объединения двух конечных множеств можно найти по формуле:
 .
.
Использованный здесь прием подсчета можно применить и для определения количества элементов в объединении любого числа множеств. Его называют методом включений и исключений. Докажем формулу включений и исключений в общем случае.
Теорема 10. Для любых конечных множеств  имеет место равенство
имеет место равенство
 , (1)
, (1)
где 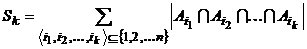 .
.
Д о к а з а т е л ь с т в о. Рассмотрим произвольный элемент  и определим вклад, который он вносит в правую часть формулы (1). Допустим, что x входит точно в m из множеств
и определим вклад, который он вносит в правую часть формулы (1). Допустим, что x входит точно в m из множеств  . Так как
. Так как 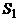 – это сумма мощностей этих множеств, то элемент x в
– это сумма мощностей этих множеств, то элемент x в 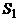 сосчитан m раз. Далее,
сосчитан m раз. Далее,  – сумма мощностей попарных пересечений множеств
– сумма мощностей попарных пересечений множеств  . Значит, x будет в этой сумме сосчитан столько раз, сколько существует пар множеств
. Значит, x будет в этой сумме сосчитан столько раз, сколько существует пар множеств  таких, что
таких, что  . Но x принадлежит точно m множествам, значит, таких пар будет
. Но x принадлежит точно m множествам, значит, таких пар будет  . Рассуждая и дальше в том же духе, приходим к выводу, что для любого
. Рассуждая и дальше в том же духе, приходим к выводу, что для любого  элемент x в сумме
элемент x в сумме  учтен
учтен 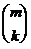 раз. Значит, общий вклад элемента x в правую часть формулы (1) равен
раз. Значит, общий вклад элемента x в правую часть формулы (1) равен  . Из свойства 6° биномиальных коэффициентов следует, что эта сумма равна
. Из свойства 6° биномиальных коэффициентов следует, что эта сумма равна  . Значит, каждый элемент сосчитан точно один раз и правая часть (1) равна числу элементов, т.е. мощности объединения множеств
. Значит, каждый элемент сосчитан точно один раз и правая часть (1) равна числу элементов, т.е. мощности объединения множеств  .
.
В качестве примера применения метода включения и исключения рассмотрим задачу о беспорядках: сколько существует перестановок 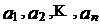 чисел
чисел  таких, что
таких, что 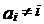 при любом
при любом 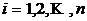 ?
?
Число искомых перестановок D является разностью между числом всех перестановок и числом перестановок, у которых хотя бы один символ стоит на своем месте. Обозначим множество перестановок, для которых  через
через 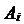 , тогда
, тогда  . Мощность объединения множеств находим по формуле включения и исключения. Пересечение любых k множеств
. Мощность объединения множеств находим по формуле включения и исключения. Пересечение любых k множеств 
 содержит все такие перестановки, у которых числа
содержит все такие перестановки, у которых числа 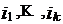 стоят на своих местах. Поскольку остальные n-k чисел располагаются на оставшихся местах произвольно, число таких перестановок равно (n-k)!. Поэтому каждое слагаемое в сумме
стоят на своих местах. Поскольку остальные n-k чисел располагаются на оставшихся местах произвольно, число таких перестановок равно (n-k)!. Поэтому каждое слагаемое в сумме 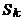 равно
равно  !. Число слагаемых равно числу способов выбрать k чисел из n, т.е.
!. Число слагаемых равно числу способов выбрать k чисел из n, т.е.  . Следовательно,
. Следовательно,  .
.
Задачи
1. На одной из кафедр университета работают тринадцать человек, причем каждый из них знает хотя бы один иностранный язык. Десять человек знают английский, семеро - немецкий, шестеро - французский. Пятеро знают английский и немецкий, четверо - английский и французский, трое - немецкий и французский.
Сколько человек знают все три языка?
Сколько человек знают ровно два языка?
Сколько человек знают только английский язык?
2. В музыкальном ансамбле используется четыре инструмента, Для каждого инструмента в ансамбле имеется четыре человека, владеющих данным инструментом, для любых двух инструментов - три человека, играющих на них, для любых трех - два человека. Один человек владеет всеми четырьмя инструментами. Сколько человек в ансамбле?
6. Задачи для самостоятельной работы
1. Имеется 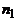 разных книг одного автора,
разных книг одного автора, 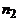 – второго и
– второго и  – третьего. Каким числом способов можно выбрать
– третьего. Каким числом способов можно выбрать
а) две книги одного автора?
б) три книги одного автора?
в) одну книгу первого автора, две – второго и три – третьего?
2. Каким числом способов можно на шахматной доске поместить черного и белого королей так, чтобы они не атаковали друг друга?
3. На одной из двух параллельных прямых зафиксировано n точек, а на другой - m точек. Сколько имеется
а) треугольников;
б) четырехугольников
с вершинами в данных точках?
4. Каким числом способов из 10 человек можно выбрать три комиссии, если в первой и во второй должно быть по 3 человека, а в третьей - 5 человек, и ни один из членов первой комиссии не должен входить во вторую и третью?
5. Траекторией назовем ломаную линию на плоскости, состоящую из отрезков, параллельных координатным осям, причем длины отрезков - целые числа, а при движении вдоль ломаной от начальной точки каждый вертикальный отрезок проходится снизу вверх, а горизонтальный - слева направо. Найдите число траекторий, начинающихся в точке (0,0), а оканчивающихся
а) в точке (m,n);
б) на прямой  .
.
6. Сколько диагоналей у выпуклого n -угольника? Найдите число точек пересечения этих диагоналей (не считая вершин), если известно, что в каждой из этих точек пересекаются только две диагонали?
7. Имеется колода из 4 n карт четырех мастей, по n карт каждой масти, занумерованных числами 1,2,...,n. Каким числом способов можно выбрать пять карт так, чтобы среди них оказались:
а) пять карт одной масти с последовательными номерами;
б) четыре карты с одинаковыми номерами;
в) три карты с одним номером и две с другим;
г) пять карт одной масти;
д) пять карт с последовательными номерами;
е) три карты с одинаковыми номерами;
ж) две карты с одинаковыми, остальные с разными номерами.
8. Сколько имеется шестизначных десятичных чисел, у которых
а) есть одинаковые цифры?
б) цифры идут в возрастающем порядке?
в) ровно три цифры четные?
г) не менее двух четных цифр?
д) все цифры различны, причем первая - не 9, а последняя - не 0?
е) сумма цифр четна?
9. Сколько существует отображений множества A в множество B, если ÷ A ÷= n, ÷ B ÷= m? Сколько среди них инъективных? Биективных?
10 Дано множество U из n элементов и в нем подмножество A из k элементов. Определите число подмножеств  , удовлетворяющих условию
, удовлетворяющих условию
а)  ; г)
; г)  ; ж)
; ж)  ;
;
б) 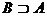 ; д)
; д) 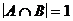 ; з)
; з)  ;
;
в)  ; е)
; е)  ; и)
; и)  .
.
11. В множестве U из n элементов, найдите число пар подмножеств (A, B) удовлетворяющих условиям:
а)  ; г)
; г)  ,
,  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  ,
,  ,
, 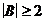 .
.
12. Определите число матриц с m строками и n столбцами, составленных из элементов 0 и 1, у которых строки попарно различны.
13. Каким числом способов можно разложить p черных и q белых шаров по k различным ящикам?
14. Каким числом способов можно разместить n различных предметов по k различным ящикам? Сколько таких размещений, при которых в каждый ящик укладывается не более одного предмета?
15. Каким числом способов можно распределить n одинаковых монет между k лицами? Сколько таких способов, при которых каждый получает не менее одной монеты?
16. Каким числом способов можно kn различных предметов разложить по n одинаковым (неразличимым) ящикам так, чтобы в каждом ящике оказалось ровно k предметов?
17 Каким числом способов 7 человек могут разместиться в трех автомобилях, если в первом из них имеется 2 свободных места, во втором - 3, а в третьем - 4?
18. В следующих заданиях рассматриваются слова в алфавите  . Через
. Через  обозначается число вхождений буквы
обозначается число вхождений буквы 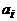 в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям.
в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям.
| Вариант
| q
| n
| Условие
|
| 1)
|
|
| n1 ?6
|
| 2)
|
|
| n1 =2n2
|
| 3)
|
|
| n1 + n2 < n3 + n4
|
| 4)
|
|
| n1 = n2 + n3 + n4
|
| 5)
|
|
| n1 = 2, n2<n3
|
| 6)
|
|
| n1 + n2 = 3, n3? 2
|
| 7)
|
|
| n1 = n2
|
| 8)
|
|
| n1 = n2 + n3, n2 - четное
|
| 9)
|
|
| n1 + n2 < n3
|
| 10)
|
|
| n1 + n2 = n3
|
| 11)
|
|
| n1 < n2
|
| 12)
|
|
| n1 + n2? 6
|
| 13)
|
|
| 2 < n1 < 6
|
| 14)
|
|
| n1? n2 ? n3
|
| 15)
|
|
| n1?2, n2 + n3 = 4
|
| 16)
|
|
| n1 = 4, n2?3
|
| 17)
|
|
| n1? n2 + n3 + n4
|
| 18)
|
|
| n1 + n2 = 3, n3?2
|
| 19)
|
|
| n1 > n2 > 2
|
| 20)
|
|
| n1 = n2
|
| 21)
|
|
| n1 + n2 = n3 + n4
|
| 22)
|
|
| n1 = 2, n2?3
|
| 23)
|
|
| n1?2, n2 + n3 + n4 = 3
|
| 24)
|
|
| n1 + n2?4, n3 = 1
|
| 25)
|
|
| n1 = n2 = n3
|
19. В группе N студентов, из них  человек владеют языком программирования СИ,
человек владеют языком программирования СИ,  - Паскалем,
- Паскалем,  - Бейсиком,
- Бейсиком,  студентов программируют на СИи Паскале,
студентов программируют на СИи Паскале, 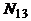 - на СИ и Бейсике,
- на СИ и Бейсике,  - на Паскале и Бейсике,
- на Паскале и Бейсике,  человек знают все три языка и
человек знают все три языка и  не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):
не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):
| Вариант
| N
| 
| 
| 
| 
| 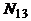
| 
| 
| 
|
| 1)
|
|
|
|
|
|
|
|
|
|
| 2)
|
|
|
|
|
|
|
|
|
|
| 3)
|
|
|
|
|
|
|
|
|
|
| 4)
|
|
|
|
|
|
|
|
|
|
| 5)
|
|
|
|
|
|
|
|
|
|
| 6)
|
|
|
|
|
|
|
|
|
|
| 7)
|
|
|
|
|
|
|
|
|
|
| 8)
|
|
|
|
|
|
|
|
|
|
| 9)
|
|
|
|
|
|
|
|
|
|
| 10)
|
|
|
|
|
|
|
|
|
|
| 11)
|
|
|
|
|
|
|
|
|
|
| 12)
|
|
|
|
|
|
|
|
|
|
| 13)
|
|
|
|
|
|
|
|
|
|
| 14)
|
|
|
|
|
|
|
|
|
|
| 15)
|
|
|
|
|
|
|
|
|
|
| 16)
|
|
|
|
|
|
|
|
|
|
| 17)
|
|
|
|
|
|
|
|
|
|
| 18)
|
|
|
|
|
|
|
|
|
|
| 19)
|
|
|
|
|
|
|
|
|
|
| 20)
|
|
|
|
|
|
|
|
|
|
| 21)
|
|
|
|
|
|
|
|
|
|
| 22)
|
|
|
|
|
|
|
|
|
|
| 23)
|
|
|
|
|
|
|
|
|
|
| 24)
|
|
|
|
|
|
|
|
|
|
| 25)
|
|
|
|
|
|
|
|
|
|





 некоторые элементы из множества
некоторые элементы из множества  сосчитаны дважды. Это те элементы, которые принадлежат пересечению
сосчитаны дважды. Это те элементы, которые принадлежат пересечению  . Следовательно, мощность объединения двух конечных множеств можно найти по формуле:
. Следовательно, мощность объединения двух конечных множеств можно найти по формуле: .
. имеет место равенство
имеет место равенство , (1)
, (1)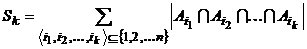 .
. и определим вклад, который он вносит в правую часть формулы (1). Допустим, что x входит точно в m из множеств
и определим вклад, который он вносит в правую часть формулы (1). Допустим, что x входит точно в m из множеств 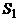 – это сумма мощностей этих множеств, то элемент x в
– это сумма мощностей этих множеств, то элемент x в  – сумма мощностей попарных пересечений множеств
– сумма мощностей попарных пересечений множеств  . Значит, x будет в этой сумме сосчитан столько раз, сколько существует пар множеств
. Значит, x будет в этой сумме сосчитан столько раз, сколько существует пар множеств  таких, что
таких, что  . Но x принадлежит точно m множествам, значит, таких пар будет
. Но x принадлежит точно m множествам, значит, таких пар будет  . Рассуждая и дальше в том же духе, приходим к выводу, что для любого
. Рассуждая и дальше в том же духе, приходим к выводу, что для любого  элемент x в сумме
элемент x в сумме  учтен
учтен 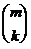 раз. Значит, общий вклад элемента x в правую часть формулы (1) равен
раз. Значит, общий вклад элемента x в правую часть формулы (1) равен  . Из свойства 6° биномиальных коэффициентов следует, что эта сумма равна
. Из свойства 6° биномиальных коэффициентов следует, что эта сумма равна  . Значит, каждый элемент сосчитан точно один раз и правая часть (1) равна числу элементов, т.е. мощности объединения множеств
. Значит, каждый элемент сосчитан точно один раз и правая часть (1) равна числу элементов, т.е. мощности объединения множеств 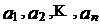 чисел
чисел  таких, что
таких, что 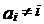 при любом
при любом 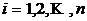 ?
? через
через 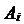 , тогда
, тогда  . Мощность объединения множеств находим по формуле включения и исключения. Пересечение любых k множеств
. Мощность объединения множеств находим по формуле включения и исключения. Пересечение любых k множеств 
 содержит все такие перестановки, у которых числа
содержит все такие перестановки, у которых числа 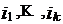 стоят на своих местах. Поскольку остальные n-k чисел располагаются на оставшихся местах произвольно, число таких перестановок равно (n-k)!. Поэтому каждое слагаемое в сумме
стоят на своих местах. Поскольку остальные n-k чисел располагаются на оставшихся местах произвольно, число таких перестановок равно (n-k)!. Поэтому каждое слагаемое в сумме 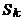 равно
равно  !. Число слагаемых равно числу способов выбрать k чисел из n, т.е.
!. Число слагаемых равно числу способов выбрать k чисел из n, т.е.  . Следовательно,
. Следовательно,  .
.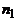 разных книг одного автора,
разных книг одного автора, 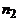 – второго и
– второго и  – третьего. Каким числом способов можно выбрать
– третьего. Каким числом способов можно выбрать .
. , удовлетворяющих условию
, удовлетворяющих условию ; г)
; г)  ; ж)
; ж)  ;
;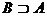 ; д)
; д) 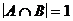 ; з)
; з)  ;
; ; е)
; е)  ; и)
; и)  .
. ,
,  ;
; ,
, 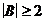 .
. . Через
. Через  обозначается число вхождений буквы
обозначается число вхождений буквы 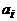 в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям.
в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям. человек владеют языком программирования СИ,
человек владеют языком программирования СИ,  - Паскалем,
- Паскалем,  - Бейсиком,
- Бейсиком,  студентов программируют на СИи Паскале,
студентов программируют на СИи Паскале, 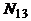 - на СИ и Бейсике,
- на СИ и Бейсике,  - на Паскале и Бейсике,
- на Паскале и Бейсике,  человек знают все три языка и
человек знают все три языка и  не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):
не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):



