РЕШЕНИЕ ЗАДАЧ ПО АЛГЕБРЕ
ДЛЯ 2 КУРСА ОЗО
ФАКУЛЬТЕТА МАТЕМАТИКИ
И ИНФОРМАТИКИ
Тула 1999
Рецензент -
канд. физ.-мат. наук, доцент, зав. кафедрой математического анализа
ТГПУ им. Л. Н. Толстого И. В. Денисов
Решение задач по алгебре для 2 курса ОЗО факультета математики и информатики
Методические рекомендации предназначены для студентов 2 курса ОЗО факультета математики и информатики. Приведены основные теоретические сведения, необходимые для решения задач. Разобраны решения типовых заданий. Приведены упражнения для решения на практических занятиях. Даны задания для контрольных работ.
Составитель -
канд. физ.-мат. наук, доцент кафедры алгебры и геометрии ТГПУ им. Л. Н. Толстого
Ю. А. Игнатов
Учебное издание
Решение задач по алгебре для 2 курса ОЗО факультета математики и информатики
Составитель
ИГНАТОВ Юрий Александрович
Формат 60 ´ 84 / 16. Бумага офс.
Усл. печ. л. 0,93. Уч.-изд. л. 1,4. Тираж 50 экз. Изд. № 3© Ю. Игнатов, 1999 г.
Системы линейных уравнений
Для решения системы линейных уравнений используется метод Гаусса, заключающийся в последовательном исключении переменных. Для удобства систему

записываем в виде матрицы, построенной из коэффициентов и свободных членов системы. При этом столбец свободных членов отделяется от остальных столбцов вертикальной чертой. Матрица имеет вид

Над системой допускается производить следующие элементарные преобразования, которые приводят к равносильной системе:
1) умножение какого-либо уравнения на скаляр l ¹ 0;
2) прибавление к уравнению другого уравнения, умноженного на скаляр l;
3) исключение из системы или добавление к ней уравнения с нулевыми коэффициентами и свободным членом.
Соответствующие преобразования производятся над строками матрицы системы. Преобразования приводят к эквивалентным матрицам, переходы обозначаются знаком эквивалентности ~.
Первый ненулевой коэффициент в каждой строке называем ведущим.
Цель преобразований - избавиться от переменной x1 во всех уравнениях, кроме первого. Считаем, что в первой строке ведущий элемент - a11. В противном случае поставим на первое место другую строку. Используем первую строку как опорную.
Чтобы избавиться от первого коэффициента ai1 в i-ой строке, прибавляем к этой строке первую строку, умноженную на –ai1/a11. Проделав это со всеми строками, начиная со второй, во всех этих строках на первом месте получим 0.
Возможно, что при этом станут нулевыми все элементы не только в первом столбце, но и в нескольких следующих (без первой строки). Если же какие-нибудь ненулевые элементы в получившейся матрице останутся, то повторяем указанные преобразования с матрицей, получающейся отбрасыванием первой строки и всех столбцов до первого ненулевого.
Проделав указанные преобразования, сколько возможно, получим матрицу в ступенчатом виде. Он характеризуется тем, что ведущий элемент в каждой строке, начиная со второй, расположен правее, чем в предыдущей.
Если в последней ненулевой строке ступенчатой матрицы слева от черты стоят нули, а справа ненулевой элемент, то соответствующая система решений не имеет, то есть является несовместной.
Если такой строки в ступенчатой матрице нет, то для удобства обведем ведущие элементы во всех строках в кружки. Переменные, которым соответствуют кружки, считаются базисными, остальные – свободными. Если свободных переменных нет, то система имеет единственное решение. Для его нахождения по строкам получившейся матрицы восстанавливаем уравнения, начиная с последней, и последовательно находим значения всех переменных.
Если в системе есть свободные переменные, то придаем им произвольные значения, считая параметрами. Базисные переменные выражаются через них в том же порядке, как в предыдущем случае. Система в этом случае является неопределенной, то есть имеет больше одного решения.
П р и м е р 1. Решить систему

Р е ш е н и е. Строим матрицу системы и приводим ее к ступенчатому виду:


 ~
~  ~
~  .
.
Ко второй и третьей строкам первой матрицы прибавлялась первая строка, умноженная на –2 и –3 соответственно. К третьей строке второй матрицы прибавлялась вторая строка, умноженная на –2.
Базисными являются переменные x1 и x3, свободными x2 и x4. Полагаем
x2 = a, x4 = b. Тогда из уравнения, соответствующего второй строке ступенчатой матрицы, получаем – x3 – 2b = –1, и x3 = – 2b + 1. Подставляя в первое уравнение, получаем
x1 + 2a + 3(– 2b + 1) – b = 1, x1 = – 2a + 7b – 2.
Ответ: x1 = – 2a + 7b – 2, x2 = a, x3 = – 2b + 1, x4 = b, a, b Îℝ.
У п р а ж н е н и е 1. Решите системы:
а) 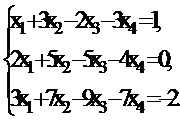
б) 
в) 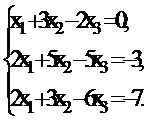
г) 
Алгебра матриц
На множестве матриц определены операции сложения, умножения на скаляры, умножения матриц.
Складывать можно прямоугольные матрицы одного и того же порядка. Сложение выполняется покомпонентно.
Умножать на скаляр можно любую матрицу. Умножение выполняется покомпонентно (то есть каждый элемент матрицы умножается на скаляр).
Умножать можно матрицу порядка m´k на матрицу порядка k´n, то есть длина строки первой матрицы должна быть равна длине столбца второй матрицы В произведении получится матрица порядка m´n. Ее элемент, находящийся в i-ой строке и j-ом столбце, получается умножением элементов i-ой строки первой матрицы на соответствующие элементы j-ого столбца второй матрицы и сложением получившихся произведений.
П р и м е р 4.1.

 =
= 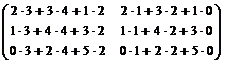 =
=  .
.
Матрицей, транспонированной к матрице А, называется матрица АТ, строки которой совпадают с соответствующими столбцами матрицы А.
Обратной к квадратной матрице А называется матрица А-1 такая, что
А×А-1 = А-1×А = Е, где Е – единичная матрица,
Е =  .
.
Для нахождения обратной матрицы к матрице А строим новую матрицу, расположив рядом матрицы А и Е и отделив их друг от друга вертикальной чертой. Соответствующие строки матриц А и Е образуют единую строку новой матрицы. Элементарными преобразованиями строк приводим матрицу А к единичному виду. Тогда матрица Е преобразуется к А-1.
П р и м е р 4.2. Найти матрицу, обратную к матрице
А =  .
.
Р е ш е н и е. Объединяем матрицы А и Е и приводим матрицу А к единичной:
 ~
~  ~
~
~  ~
~  ~
~
~  ~
~  .
.
Следовательно,
А-1 =  .
.
У п р а ж н е н и е 4.1 Найти обратную матрицу:
а)  ; б)
; б)  ; в)
; в)  .
.
У п р а ж н е н и е 4.2. Решить матричное уравнение:
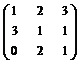 X =
X =  .
.
Определители
Определители второго и третьего порядка вычисляются по формулам
 = ad – bc;
= ad – bc;
 = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32.
= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32.
Для вычисления определителей более высокого порядка их порядок следует понизить. Для этого пользуются правилами:
1) если к строке (столбцу) матрицы прибавить другую строку (столбец), умноженную на произвольный скаляр, то ее определитель не изменится;
2) если строку (столбец) матрицы умножить на скаляр l, то на l умножится ее определитель;
3) если поменять местами две строки (столбца) матрицы, то ее определитель поменяет знак;
4) определитель матрицы с нулевой строкой (столбцом) равен 0;
5) определитель матрицы А, у которой все элементы какой-либо строки (столбца), кроме, может быть, aij, равны 0, равен (-1)i+jaijMij, где Mij – определитель матрицы, полученной из А вычеркиванием i-ой строки и j-го столбца.
Для понижения порядка определителя выбираем в нем какой-нибудь элемент, обычно равный 1. Используя строку, в которой он стоит, как опорную, с помощью правила 1) как в методе Гаусса заменяем остальные элементы столбца, в котором стоит выбранный элемент, на нули. После этого понижаем порядок определителя по правилу 5). Можно и поменять строки и столбцы ролями, делая нули не в столбце, а в строке.
П р и м е р 5.1. Вычислить определитель
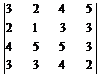 .
.
Р е ш е н и е. Мы имеем элемент 1 на пересечении второй строки и второго столбца. Используя вторую строку, сделаем остальные элементы во втором столбце равными 0. Для этого к первой, третьей и четвертой строкам прибавляем вторую, умноженную на –2, -5, -3 соответственно. Получаем:
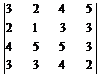 =
=  =(-1)2+2
=(-1)2+2 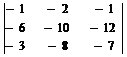 =
=  =
=
= 42 + 12 + 0 – 18 – 16 – 0 = 20.
Перед вычислением определителя третьего порядка его упростили, прибавив ко второй строке третью, умноженную на –2.
У п р а ж н е н и е 5.1. Вычислить определители:
а)  ; б)
; б)  ; в)
; в)  .
.
Минором элемента aij квадратной матрицы А называется определитель матрицы, полученной из А вычеркиванием i-ой строки и j-ого столбца (в которых стоит элемент aij).
Алгебраическим дополнением элемента aij квадратной матрицы А называется скаляр Aij = (-1)i+j Mij, где Mij – минор элемента aij.
Матрицу, обратную к матрице А, можно вычислить по формуле
A-1 = ïAï-1 A*,
где A* – матрица, полученная из А заменой каждого элемента его алгебраическим дополнением и последующим транспонированием.
П р и м е р 5.2. Найти матрицу, обратную к
А =  .
.
Р е ш е н и е. Имеем
ïAï = 6 + 18 + 60 – 9 – 16 – 45 = 14;
A* =  ;
;
A-1 =  .
.
У п р а ж н е н и е 5.2. Найти обратную матрицу методом алгебраических дополнений:
а) 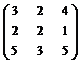 ; б)
; б) 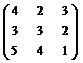 .
.
Евклидово пространство
Евклидовым пространством называется линейное пространство над полем R, в котором определено скалярное умножение, ставящее в соответствие каждой паре векторов  ,
,  скаляр
скаляр 
 , причем выполнены условия:
, причем выполнены условия:
1) 
 =
= 
 ;
;
2) (a  + b
+ b  )
)  = a(
= a(
 ) + b(
) + b(
 );
);
3)  ¹
¹  Þ
Þ 
 > 0.
> 0.
Стандартное скалярное произведение вычисляется по формулам
(a1, …, an) (b1, …, bn) = a1b1 + … + anbn.
Векторы  и
и  называются ортогональными, записывается
называются ортогональными, записывается  ^
^  , если их скалярное произведение равно 0.
, если их скалярное произведение равно 0.
Система векторов называется ортогональной, если векторы в ней попарно ортогональны.
Ортогональная система векторов линейно независима.
Процесс ортогонализации системы векторов  , …,
, …,  заключается в переходе к эквивалентной ортогональной системе
заключается в переходе к эквивалентной ортогональной системе  , …,
, …,  , выполняемом по формулам:
, выполняемом по формулам:
 =
=  ;
;
 , где
, где  , k = 2, …, n.
, k = 2, …, n.
П р и м е р 7.1. Ортогонализировать систему векторов
 = (1, 2, 2, 1),
= (1, 2, 2, 1),  = (3, 2, 1, 1),
= (3, 2, 1, 1),  = (4, 1, 3, -2).
= (4, 1, 3, -2).
Р е ш е н и е. Имеем  =
=  = (1, 2, 2, 1);
= (1, 2, 2, 1);
 ,
,  =
=  =
=  = 1;
= 1;
 = (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).
= (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).
 ,
,  =
=  =
=  =1;
=1;
 =
=  =1;
=1;
 = (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
= (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
У п р а ж н е н и е 7.1. Ортогонализировать системы векторов:
а)  = (1, 1, 0, 2),
= (1, 1, 0, 2),  = (3, 1, 1, 1),
= (3, 1, 1, 1),  = (-1, -3, 1, -1);
= (-1, -3, 1, -1);
б)  = (1, 2, 1, 1),
= (1, 2, 1, 1),  = (3, 4, 1, 1),
= (3, 4, 1, 1),  = (0, 3, 2, -1).
= (0, 3, 2, -1).
П р и м е р 7.2. Дополнить систему векторов  = (1, -1, 1, -1),
= (1, -1, 1, -1),
 = (1, 1, -1, -1), до ортогонального базиса пространства.
= (1, 1, -1, -1), до ортогонального базиса пространства.
Р е ш е н и е. Исходная система ортогональна, поэтому задача имеет смысл. Так как векторы заданы в четырехмерном пространстве, то требуется найти еще два вектора. Третий вектор  = (x1, x2, x3, x4) определяем из условий
= (x1, x2, x3, x4) определяем из условий 
 = 0,
= 0, 
 = 0. Эти условия дают систему уравнений, матрица которой образована из координатных строк векторов
= 0. Эти условия дают систему уравнений, матрица которой образована из координатных строк векторов  и
и  . Решаем систему:
. Решаем систему:

 ~
~  ~
~  .
.
Свободным переменным x3 и x4 можно придать любой набор значений, отличный от нулевого. Полагаем, например, x3 = 0, x4 = 1. Тогда x2 = 0, x1 = 1, и  = (1, 0, 0, 1).
= (1, 0, 0, 1).
Аналогично находим  = (y1, y2, y3, y4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:
= (y1, y2, y3, y4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:

 ~
~  ~
~  .
.
Для свободной переменной y3 полагаем y3 = 1. Тогда y4 = 0, y2 = 1, y1= 0, и  = (0, 1, 1, 0).
= (0, 1, 1, 0).
Нормой вектора  евклидова пространства называется неотрицательное действительное число
евклидова пространства называется неотрицательное действительное число  .
.
Вектор называется нормированным, если его норма равна 1.
Чтобы нормировать вектор, его следует разделить на его норму.
Ортогональная система нормированных векторов называется ортонормированной.
У п р а ж н е н и е 7.2. Дополнить систему векторов до ортонормированного базиса пространства:
а)  = (1/2, 1/2, 1/2, 1/2),
= (1/2, 1/2, 1/2, 1/2),  = (-1/2, 1/2, -1/2, 1/2);
= (-1/2, 1/2, -1/2, 1/2);
б)  = (1/3, -2/3, 2/3).
= (1/3, -2/3, 2/3).
Линейные отображения
Пусть U и V – линейные пространства над полем F. Отображение f: U ® V называется линейным, если  и
и  .
.
П р и м е р 8.1. Являются ли линейными преобразования трехмерного пространства:
а) f(x1, x2, x3) = (2x1, x1 – x3, 0);
б) f(x1, x2, x3) = (1, x1 + x2, x3).
Р е ш е н и е.
а) Имеем f((x1, x2, x3) + (y1, y2, y3)) = f(x1 + y1, x2 + y2, x3 + y3) =
= (2(x1 + y1), (x1 + y1) – (x3 + y3), 0) = (2x1, x1 – x3, 0) + (2y1, y1 - y3, 0) =
= f((x1, x2, x3) + f(y1, y2, y3));
f(l(x1, x2, x3)) = f(lx1, lx2, lx3) = (2lx1, lx1 – lx3, 0) = l(2x1, x1 – x3, 0) =
= l f(x1, x2, x3).
Следовательно, преобразование является линейным.
б) Имеем f((x1, x2, x3) + (y1, y2, y3)) = f(x1 + y1, x2 + y2, x3 + y3) =
= (1, (x1 + y1) + (x2 + y2), x3 + y3);
f((x1, x2, x3) + f(y1, y2, y3)) = (1, x1 + x2, x3) + (1, y1 + y2, y3) =
= (2, (x1 + y1) + (x2 + y2), x3 + y3) ¹ f((x1, x2, x3) + (y1, y2, y3)).
Следовательно, преобразование не является линейным.
Образом линейного отображения f: U ® V называется множество образов векторов из U, то есть
Im (f) = {f( ) ï
) ï  Î U}.
Î U}.
Ядром линейного отображения f: U ® V называется множество векторов из U, отображающихся в  , то есть
, то есть
Ker (f) = {  Î Uï f(
Î Uï f( ) =
) =  }.
}.
Im (f) и Ker (f) являются подпространствами в пространствах V и U соответственно. Их размерности называются рангом и дефектом линейного отображения f и обозначаются rank f и def f соответственно.
Ранг и дефект линейного отображения f: U ® V связаны соотношением
rank f + def f = dim U.
Пусть задано линейное отображение f: U ® V, и  , …,
, …,  ;
;  , …,
, …,  – базисы пространств U и V соответственно. Пусть
– базисы пространств U и V соответственно. Пусть
f( ) = a11
) = a11  + … + am1
+ … + am1  ;
;
………………………………
f( ) = a1n
) = a1n  + … + anm
+ … + anm  .
.
Матрицей линейного отображения f называется матрица
A =  .
.
Образ любого вектора  можно найти с помощью матричного умножения: f(
можно найти с помощью матричного умножения: f( ) = А
) = А  , где
, где  записан в виде столбца.
записан в виде столбца.
П р и м е р 8.2. Найти ранг, дефект, базисы образа и ядра линейного отображения f, заданного матрицей
А =  .
.
Р е ш е н и е. Образ отображения порождается образами базисных векторов, расположенных по столбцам матрицы А. Поэтому базис образа – это базис системы столбцов. Находим его приведением матрицы к ступенчатому виду:

 ~
~  ~
~  .
.
Заключаем, что базис Im f образуют векторы (1, 2, 2), (2, 5, 3) и (1, 3, 2). Следовательно, rank f = 3. Исходное пространство имеет размерность 4 (число столбцов матрицы), поэтому def f = 4 – rank f = 1.
Ядро отображения – это множество решений уравнения А  =
=  , базис ядра – фундаментальная система решений соответствующей системы линейных уравнений. Матрица системы уже приведена к ступенчатому виду. Полагаем
, базис ядра – фундаментальная система решений соответствующей системы линейных уравнений. Матрица системы уже приведена к ступенчатому виду. Полагаем
x3 = a, тогда x4 = 0, x2 = -a, x1 = -a,  = (-a, -a, a, 0) = a(-1, -1, 1, 0). Таким образом, базис ядра образует вектор (-1, -1, 1, 0).
= (-a, -a, a, 0) = a(-1, -1, 1, 0). Таким образом, базис ядра образует вектор (-1, -1, 1, 0).
З а м е ч а н и е. Если будет получено, что def f = 0, то ядро будет нулевым пространством и не имеет базиса.
У п р а ж н е н и е 8.1. Найти ранг, дефект, базисы образа и ядра линейного отображения f, заданного матрицей:
а) А =  ; б) А =
; б) А =  ; в) А =
; в) А =  .
.
Задания к контрольной работе
В качестве a и b возьмите соответственно предпоследнюю и последнюю цифры номера зачетной книжки.
1. Найти частное решение неоднородной системы и фундаментальную систему решений ассоциированной однородной системы

2. Найти базис системы векторов  = (1, 3, 2, 2),
= (1, 3, 2, 2),  = (2, 5, 3, 2),
= (2, 5, 3, 2),
 = (0, 1, 1, 2),
= (0, 1, 1, 2),  = (2, a, 1, b) и выразить остальные векторы через базис.
= (2, a, 1, b) и выразить остальные векторы через базис.
3. Найти обратную к матрице А и проверить результат, умножив А на А-1:
А =  .
.
4.Вычислить определитель:

5. Найти базис и размерность суммы и пересечения подпространств, натянутых на следующие системы векторов:

6. Ортогонализировать систему векторов:
 = (1, 1, 0, -2),
= (1, 1, 0, -2),  = (2, 2, b, -1),
= (2, 2, b, -1),  = (a+3, -a+1, b, -1).
= (a+3, -a+1, b, -1).
7. Найти ранг, дефект, базисы образа и ядра линейного отображения f, заданного матрицей
А =  .
.
8. Найдите собственные векторы и собственные значения линейного оператора, заданного матрицей
А =  .
.
Содержание
1. Системы линейных уравнений............................................... 1
2. Линейная зависимость. Базис системы векторов................. 4
3. Фундаментальная система решений...................................... 6
4. Алгебра матриц......................................................................... 7
5. Определители............................................................................. 9
6. Линейные пространства. Подпространства. Размерность и базис 12
7. Евклидово пространство........................................................ 14
8. Линейные отображения......................................................... 16
9. Собственные векторы и собственные значения................. 19
Задания к контрольной работе........................................................................... 20
РЕШЕНИЕ ЗАДАЧ ПО АЛГЕБРЕ
ДЛЯ 2 КУРСА ОЗО
ФАКУЛЬТЕТА МАТЕМАТИКИ
И ИНФОРМАТИКИ
Тула 1999
Рецензент -
канд. физ.-мат. наук, доцент, зав. кафедрой математического анализа
ТГПУ им. Л. Н. Толстого И. В. Денисов
Решение задач по алгебре для 2 курса ОЗО факультета математики и информатики
Методические рекомендации предназначены для студентов 2 курса ОЗО факультета математики и информатики. Приведены основные теоретические сведения, необходимые для решения задач. Разобраны решения типовых заданий. Приведены упражнения для решения на практических занятиях. Даны задания для контрольных работ.
Составитель -
канд. физ.-мат. наук, доцент кафедры алгебры и геометрии ТГПУ им. Л. Н. Толстого
Ю. А. Игнатов
Учебное издание
Решение задач по алгебре для 2 курса ОЗО факультета математики и информатики
Составитель
ИГНАТОВ Юрий Александрович
Формат 60 ´ 84 / 16. Бумага офс.
Усл. печ. л. 0,93. Уч.-изд. л. 1,4. Тираж 50 экз. Изд. № 3© Ю. Игнатов, 1999 г.
Системы линейных уравнений
Для решения системы линейных уравнений используется метод Гаусса, заключающийся в последовательном исключении переменных. Для удобства систему

записываем в виде матрицы, построенной из коэффициентов и свободных членов системы. При этом столбец свободных членов отделяется от остальных столбцов вертикальной чертой. Матрица имеет вид

Над системой допускается производить следующие элементарные преобразования, которые приводят к равносильной системе:
1) умножение какого-либо уравнения на скаляр l ¹ 0;
2) прибавление к уравнению другого уравнения, умноженного на скаляр l;
3) исключение из системы или добавление к ней уравнения с нулевыми коэффициентами и свободным членом.
Соответствующие преобразования производятся над строками матрицы системы. Преобразования приводят к эквивалентным матрицам, переходы обозначаются знаком эквивалентности ~.
Первый ненулевой коэффициент в каждой строке называем ведущим.
Цель преобразований - избавиться от переменной x1 во всех уравнениях, кроме первого. Считаем, что в первой строке ведущий элемент - a11. В противном случае поставим на первое место другую строку. Используем первую строку как опорную.
Чтобы избавиться от первого коэффициента ai1 в i-ой строке, прибавляем к этой строке первую строку, умноженную на –ai1/a11. Проделав это со всеми строками, начиная со второй, во всех этих строках на первом месте получим 0.
Возможно, что при этом станут нулевыми все элементы не только в первом столбце, но и в нескольких следующих (без первой строки). Если же какие-нибудь ненулевые элементы в получившейся матрице останутся, то повторяем указанные преобразования с матрицей, получающейся отбрасыванием первой строки и всех столбцов до первого ненулевого.
Проделав указанные преобразования, сколько возможно, получим матрицу в ступенчатом виде. Он характеризуется тем, что ведущий элемент в каждой строке, начиная со второй, расположен правее, чем в предыдущей.
Если в последней ненулевой строке ступенчатой матрицы слева от черты стоят нули, а справа ненулевой элемент, то соответствующая система решений не имеет, то есть является несовместной.
Если такой строки в ступенчатой матрице нет, то для удобства обведем ведущие элементы во всех строках в кружки. Переменные, которым соответствуют кружки, считаются базисными, остальные – свободными. Если свободных переменных нет, то система имеет единственное решение. Для его нахождения по строкам получившейся матрицы восстанавливаем уравнения, начиная с последней, и последовательно находим значения всех переменных.
Если в системе есть свободные переменные, то придаем им произвольные значения, считая параметрами. Базисные переменные выражаются через них в том же порядке, как в предыдущем случае. Система в этом случае является неопределенной, то есть имеет больше одного решения.
П р и м е р 1. Решить систему

Р е ш е н и е. Строим матрицу системы и приводим ее к ступенчатому виду:


 ~
~  ~
~  .
.
Ко второй и третьей строкам первой матрицы прибавлялась первая строка, умноженная на –2 и –3 соответственно. К третьей строке второй матрицы прибавлялась вторая строка, умноженная на –2.
Базисными являются переменные x1 и x3, свободными x2 и x4. Полагаем
x2 = a, x4 = b. Тогда из уравнения, соответствующего второй строке ступенчатой матрицы, получаем – x3 – 2b = –1, и x3 = – 2b + 1. Подставляя в первое уравнение, получаем
x1 + 2a + 3(– 2b + 1) – b = 1, x1 = – 2a + 7b – 2.
Ответ: x1 = – 2a + 7b – 2, x2 = a, x3 = – 2b + 1, x4 = b, a, b Îℝ.
У п р а ж н е н и е 1. Решите системы:
а) 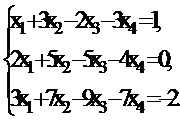
б) 
в) 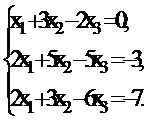
г) 
Линейная зависимость. Базис системы векторов
Линейной комбинацией векторов  называется вектор
называется вектор  , где λ1,..., λm – произвольные коэффициенты.
, где λ1,..., λm – произвольные коэффициенты.
Система векторов  называется линейно зависимой, если существует ее линейная комбинация, равная
называется линейно зависимой, если существует ее линейная комбинация, равная  , в которой есть хотя бы один ненулевой коэффициент.
, в которой есть хотя бы один ненулевой коэффициент.
Система векторов  называется линейно независимой, если в любой ее линейной комбинации, равной
называется линейно независимой, если в любой ее линейной комбинации, равной  , все коэффициенты нулевые.
, все коэффициенты нулевые.
Базисом системы векторов  называется ее непустая линейно независимая подсистема, через которую можно выразить любой вектор системы.
называется ее непустая линейно независимая подсистема, через которую можно выразить любой вектор системы.
П р и м е р 2. Найти базис системы векторов  = (1, 2, 2, 4),
= (1, 2, 2, 4),  = (2, 3, 5, 1),
= (2, 3, 5, 1),  = (3, 4, 8, -2),
= (3, 4, 8, -2),  = (2, 5, 0, 3) и выразить остальные векторы через базис.
= (2, 5, 0, 3) и выразить остальные векторы через базис.
Р е ш е н и е. Строим матрицу, в которой координаты данных векторов располагаем по столбцам. Приводим ее к ступенчатому виду.

 ~
~  ~
~  ~
~  .
.
Базис данной системы образуют векторы  ,
,  ,
,  , которым соответствуют ведущие элементы строк, выделенные кружками. Для выражения вектора
, которым соответствуют ведущие элементы строк, выделенные кружками. Для выражения вектора  решаем уравнение x1
решаем уравнение x1  + x2
+ x2  + x4
+ x4  =
=  . Оно сводится к системе линейных уравнений, матрица которой получается из исходной перестановкой столбца, соответствующего
. Оно сводится к системе линейных уравнений, матрица которой получается из исходной перестановкой столбца, соответствующего  , на место столбца свободных членов. Поэтому для решения системы используем полученную матрицу в ступенчатом виде, сделав в ней необходимые перестановки.
, на место столбца свободных членов. Поэтому для решения системы используем полученную матрицу в ступенчатом виде, сделав в ней необходимые перестановки.

Последовательно находим:
x4 = 0;
x2 = 2;
x1 + 4 = 3, x1 = -1;
 = -
= -  + 2
+ 2  .
.
Замечание 1. Если требуется выразить через базис несколько векторов, то для каждого из них строится соответствующая система линейных уравнений. Эти системы будут отличаться только столбцами свободных членов. Поэтому для их решения можно составить одну матрицу, в которой будет несколько столбцов свободных членов. При этом каждая система решается независимо от остальных.
Замечание 2. Для выражения любого вектора достаточно использовать только базисные векторы системы, стоящие перед ним. При этом нет необходимости переформировывать матрицу, достаточно поставить вертикальную черту в нужном месте.
У п р а ж н е н и е 2. Найти базис системы векторов и выразить остальные векторы через базис:
а)  = (1, 3, 2, 0),
= (1, 3, 2, 0),  = (3, 4, 2, 1),
= (3, 4, 2, 1),  = (1, -2, -2, 1),
= (1, -2, -2, 1),  = (3, 5, 1, 2);
= (3, 5, 1, 2);
б)  = (2, 1, 2, 3),
= (2, 1, 2, 3),  = (1, 2, 2, 3),
= (1, 2, 2, 3),  = (3, -1, 2, 2),
= (3, -1, 2, 2),  = (4, -2, 2, 2);
= (4, -2, 2, 2);
в)  = (1, 2, 3),
= (1, 2, 3),  = (2, 4, 3),
= (2, 4, 3),  = (3, 6, 6),
= (3, 6, 6),  = (4, -2, 1);
= (4, -2, 1);  = (2, -6, -2).
= (2, -6, -2).







 ~
~  ~
~  .
.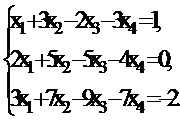

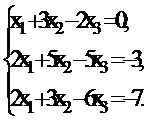


 =
= 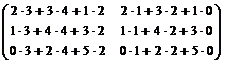 =
=  .
. .
. .
. ~
~  ~
~ ~
~  ~
~ ~
~  .
. .
. ; б)
; б)  ; в)
; в)  .
.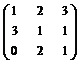 X =
X =  .
. = ad – bc;
= ad – bc; = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32.
= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32.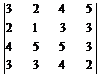 .
. =(-1)2+2
=(-1)2+2 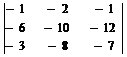 =
=  =
= ; б)
; б)  ; в)
; в)  .
. .
. ;
; .
.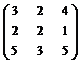 ; б)
; б) 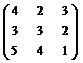 .
. ,
,  скаляр
скаляр  = a(
= a( Þ
Þ  , …,
, …,  заключается в переходе к эквивалентной ортогональной системе
заключается в переходе к эквивалентной ортогональной системе  , …,
, …,  , выполняемом по формулам:
, выполняемом по формулам: , где
, где  , k = 2, …, n.
, k = 2, …, n. = (3, 2, 1, 1),
= (3, 2, 1, 1),  = (4, 1, 3, -2).
= (4, 1, 3, -2). ,
,  =
=  =
=  = 1;
= 1; = (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).
= (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0). ,
,  =
=  =
=  =1;
=1; =
=  =1;
=1; = (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
= (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
 ~
~  ~
~  .
. = (y1, y2, y3, y4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:
= (y1, y2, y3, y4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:
 ~
~  ~
~  .
. евклидова пространства называется неотрицательное действительное число
евклидова пространства называется неотрицательное действительное число  .
. и
и  .
. ) ï
) ï  , то есть
, то есть – базисы пространств U и V соответственно. Пусть
– базисы пространств U и V соответственно. Пусть .
. .
.
 ~
~  .
. ; б) А =
; б) А =  ; в) А =
; в) А =  .
.
 = (2, 5, 3, 2),
= (2, 5, 3, 2), .
.

 .
. .
. называется вектор
называется вектор  , где λ1,..., λm – произвольные коэффициенты.
, где λ1,..., λm – произвольные коэффициенты. , в которой есть хотя бы один ненулевой коэффициент.
, в которой есть хотя бы один ненулевой коэффициент. = (2, 3, 5, 1),
= (2, 3, 5, 1),  = (3, 4, 8, -2),
= (3, 4, 8, -2),  = (2, 5, 0, 3) и выразить остальные векторы через базис.
= (2, 5, 0, 3) и выразить остальные векторы через базис.
 ~
~  ~
~  ~
~  .
.
 = (2, -6, -2).
= (2, -6, -2).