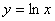Дискретный случайный вектор == случайный вектор, компоненты которого дискретные случайные величины, Закон распределения дискретного случайного вектора 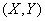 == совокупность всех возможных значений данного вектора и вероятностей
== совокупность всех возможных значений данного вектора и вероятностей  , равных
, равных  , Непрерывный случайный вектор == случайный вектор, компоненты которого непрерывные случайные величины, Функция распределения двумерной случайной величины
, Непрерывный случайный вектор == случайный вектор, компоненты которого непрерывные случайные величины, Функция распределения двумерной случайной величины 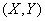 == функция двух переменных
== функция двух переменных  , равная
, равная 
Установите соответствие между левыми и правыми частями таблицы
Для построения доверительного интервала для дисперсии надо пользоваться == таблицами распределения Пирсона (  ), Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого известна, надо пользоваться == таблицами нормального распределения, Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого неизвестна, надо пользоваться == таблицами распределения Стьюдента
), Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого известна, надо пользоваться == таблицами нормального распределения, Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого неизвестна, надо пользоваться == таблицами распределения Стьюдента
Установите соответствие между названием разрыва функции y = f (x 0) в точке x 0и его определением
Неустранимый разрывIрода ==  , РазрывIIрода == Нет конечных пределов слева или справа, Устранимый разрыв ==
, РазрывIIрода == Нет конечных пределов слева или справа, Устранимый разрыв == 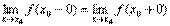 , f (x 0) не существует
, f (x 0) не существует
Установите соответствие между распределениями и формулами, их выражающие:
Биноминальное распределение ==  , Нормальное распределение ==
, Нормальное распределение ==  , Распределение Пуассона ==
, Распределение Пуассона == 
Установите соотношение между значением показателей степени и значением предела дроби 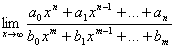
m >n==0,m<>== ∞,m = n== 
Утверждение 
верно, если 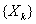 – попарно независимы и
– попарно независимы и  для всех
для всех 
Формула для коэффициента корреляции  имеет вид
имеет вид
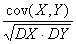
Функцией распределения двумерной случайной величины 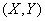 называют функцию двух переменных
называют функцию двух переменных  , равную
, равную

Функции  дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования
дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования
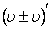 ==
==  ,
, 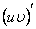 ==
==  ,
, 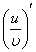 ==
== 
Функция F (x) называется первообразной для функции f (x), если для всех х
dF(x) = f(x)dx,F′(x) = f(x)
Функцияy=f(x) на интервале (а,b) является выпуклой вверх, следовательно
 , расположена ниже касательной
, расположена ниже касательной
Функцияy=f(x) на интервале (а,b) является выпуклой вниз, следовательно
 , расположена выше касательной
, расположена выше касательной
Функция 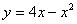 имеет максимуму в точке с координатами (набрать через запятую координаты точки):
имеет максимуму в точке с координатами (набрать через запятую координаты точки):
2,4
Функция  имеет минимум в точке с координатами (набрать через запятую координаты точки)
имеет минимум в точке с координатами (набрать через запятую координаты точки)
2,-4
Функция  имеет минимум в точке с координатами (набрать через запятую координаты точки)
имеет минимум в точке с координатами (набрать через запятую координаты точки)
1,1
Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом
F(x) =  (x)dx
(x)dx
Элементарными являются функции
 ,
,  ,
, 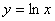
Эмпирический коэффициент корреляции между весом и ростом для выборки равен: 
Эмпирический коэффициент корреляции между весом и ростом для выборки равен:  (наберите число)
(наберите число)





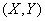 == совокупность всех возможных значений данного вектора и вероятностей
== совокупность всех возможных значений данного вектора и вероятностей  , равных
, равных  , Непрерывный случайный вектор == случайный вектор, компоненты которого непрерывные случайные величины, Функция распределения двумерной случайной величины
, Непрерывный случайный вектор == случайный вектор, компоненты которого непрерывные случайные величины, Функция распределения двумерной случайной величины  , равная
, равная 
 ), Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого известна, надо пользоваться == таблицами нормального распределения, Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого неизвестна, надо пользоваться == таблицами распределения Стьюдента
), Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого известна, надо пользоваться == таблицами нормального распределения, Для построения доверительного интервала для математического ожидания нормального распределения, дисперсия которого неизвестна, надо пользоваться == таблицами распределения Стьюдента , РазрывIIрода == Нет конечных пределов слева или справа, Устранимый разрыв ==
, РазрывIIрода == Нет конечных пределов слева или справа, Устранимый разрыв == 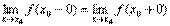 , f (x 0) не существует
, f (x 0) не существует , Нормальное распределение ==
, Нормальное распределение ==  , Распределение Пуассона ==
, Распределение Пуассона == 
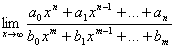


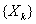 – попарно независимы и
– попарно независимы и  для всех
для всех 
 имеет вид
имеет вид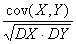
 дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования
дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования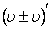 ==
==  ,
, 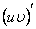 ==
==  ,
, 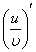 ==
== 
 , расположена ниже касательной
, расположена ниже касательной , расположена выше касательной
, расположена выше касательной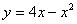 имеет максимуму в точке с координатами (набрать через запятую координаты точки):
имеет максимуму в точке с координатами (набрать через запятую координаты точки): имеет минимум в точке с координатами (набрать через запятую координаты точки)
имеет минимум в точке с координатами (набрать через запятую координаты точки) имеет минимум в точке с координатами (набрать через запятую координаты точки)
имеет минимум в точке с координатами (набрать через запятую координаты точки) (x)dx
(x)dx ,
,  ,
,