4, 3, 6, 2, 2, 3, 4, 5;, 3, 1, 3, 4, 5, 6, 4, 3;, 4, 5, 3, 1, 0, -1;, 3, 0, 7, -2,1, 4, 5;
Расположите статистические выборки в порядке возрастания размаха.
4, 1, 1, 3, 2, 3, 4, 5;, 3, 1, 3, 4, 5, 0, 4, 3;, 4, 3, 3, 1, 0, -2;, 3, 0, -2,1, 4, 5;
Расположите статистические выборки в порядке возрастания размаха.
4, 1, 1, 3, 2, 3, 4, 5;, 3, 1, 3, 4, 5, 0, 4, 3;, 4, 3, 3, 1, 0, -2;, 3, 0, -2,1, 4, 5;
Результаты наблюдений над системой (x,y) 2-х величин записаны в таблицу  Коэффициент корреляции равен: (наберите число)
Коэффициент корреляции равен: (наберите число)
-1
Результаты наблюдений над системой (x,y) двух величин записаны в таблицу  Коэффициент корреляции равен: (наберите число)
Коэффициент корреляции равен: (наберите число)
Самое маленькое значение в выборке 0, самое большое 8, медиана 2. По этой выборке построена гистограмма:

Случайная величина U, характеризующая степень расхождения теоретического и эмпирического закона распределения при проверке с помощью критерия χ2нулевой гипотезы Н0о том, что исследуемая случайная величина имеет определенный закон распределения, вычисляется по формуле

Случайная величина X принимает значения 2, -2, 0, -5, 8 с равными вероятностями. Математическое ожидание MX, равно (наберите десятичную дробь)
0,6
Случайная величина имеет плотность распределения  Тогда параметр
Тогда параметр  равен: (наберите десятичную дробь)
равен: (наберите десятичную дробь)
0,5
Случайная величина имеет показательное распределение с математическим ожиданием, равным 7. Плотность вероятности такой величины равна

Случайная величина имеет показательное распределение с плотностью  Тогда функция распределения равна
Тогда функция распределения равна

Случайная величина распределена по нормальному закону, ее математическое ожидание равно 1, а дисперсия – 25. Тогда ее функция распределения имеет вид
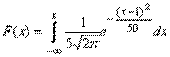
Случайная величина Х имеет биномиальное распределение с параметрами  Ее числовые характеристики таковы:
Ее числовые характеристики таковы:
 ,
, 
Случайная величина Х имеет биномиальное распределение с параметрами 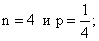 тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы:
 ,
, 
Случайная величина Х имеет биномиальное распределение с параметрами  тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы:
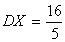 ,
, 
Случайная величина Х имеет показательное распределение с параметром  . Тогда ее функция распределения
. Тогда ее функция распределения  равна
равна

Случайная величина Х имеет распределение Пуассона с параметром 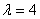 . Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)
. Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)
4,4
Случайная величина Х имеет распределение Пуассона с параметром 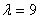 . Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)
. Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)
9,9
Случайная величина Х принимает значения –2, 1, 3, –4, 7 с равными вероятностями, тогда МХ = _____ (наберите число).
Случайная величина Х равномерно распределена на  , тогда ее математическое ожидание и дисперсия соответственно равны
, тогда ее математическое ожидание и дисперсия соответственно равны

Случайная величина Х равномерно распределена на 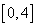 . Тогда вероятность попасть в интервал
. Тогда вероятность попасть в интервал  будет равна (наберите десятичную дробь)
будет равна (наберите десятичную дробь)
0,5
Случайная величина Х равномерно распределена на  . Тогда вероятность попасть в интервал
. Тогда вероятность попасть в интервал  будет равна: (наберите десятичную дробь)
будет равна: (наберите десятичную дробь)
0,4
Случайная величина Х распределена по биномиальному закону с параметрами  Ее числовые характеристики равны
Ее числовые характеристики равны
 ,
, 
Случайная величина Х распределена по биномиальному закону с параметрами  Ее числовые характеристики равны
Ее числовые характеристики равны

Случайная величина Х распределена по нормальному закону. Известно, что математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид

Случайная величина Х распределена равномерно на отрезке (a, b), тогда математическое ожидание и дисперсия равны
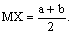 ,
, 
Случайная величина Х распределена равномерно, ее плотность равна  Тогда параметр
Тогда параметр  равен: (наберите число)
равен: (наберите число)





 Коэффициент корреляции равен: (наберите число)
Коэффициент корреляции равен: (наберите число) Коэффициент корреляции равен: (наберите число)
Коэффициент корреляции равен: (наберите число)

 Тогда параметр
Тогда параметр  равен: (наберите десятичную дробь)
равен: (наберите десятичную дробь)
 Тогда функция распределения равна
Тогда функция распределения равна
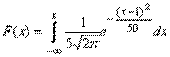
 Ее числовые характеристики таковы:
Ее числовые характеристики таковы: ,
, 
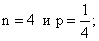 тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы: ,
, 
 тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы: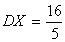 ,
, 
 . Тогда ее функция распределения
. Тогда ее функция распределения  равна
равна
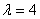 . Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)
. Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)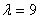 . Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую)
. Ее числовые характеристики равныMX=,DX= (набрать два числа через запятую) , тогда ее математическое ожидание и дисперсия соответственно равны
, тогда ее математическое ожидание и дисперсия соответственно равны
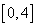 . Тогда вероятность попасть в интервал
. Тогда вероятность попасть в интервал  . Тогда вероятность попасть в интервал
. Тогда вероятность попасть в интервал  Ее числовые характеристики равны
Ее числовые характеристики равны ,
, 

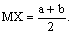 ,
, 
 Тогда параметр
Тогда параметр 


