Пусть дано  ,
, 
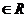 , тогда выражение вида
, тогда выражение вида 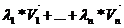 называется линейной комбинацией векторов
называется линейной комбинацией векторов 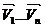 , линейная комбинация называется тривиальной, если
, линейная комбинация называется тривиальной, если 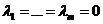 (тривиальная комбинация векторов =
(тривиальная комбинация векторов =  ).
).
Линейно независимая комбинация векторов – система векторов  называется линейно независимой, если только тривиальная комбинация этой системы равна нулевому вектору.
называется линейно независимой, если только тривиальная комбинация этой системы равна нулевому вектору.
Линейно зависимая комбинация векторов - система векторов  называется линейно зависимой, если в линейной комбинации этих векторов равной нулевому вектору есть хотя бы один не нулевой коэффициент.
называется линейно зависимой, если в линейной комбинации этих векторов равной нулевому вектору есть хотя бы один не нулевой коэффициент.
Свойства линейной комбинации векторов:
1) пусть  содержит линейно зависимую подсистему векторов
содержит линейно зависимую подсистему векторов 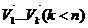 , тогда система
, тогда система  является линейно зависимой.
является линейно зависимой.
Доказательство:
Система векторов 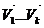 линейно зависимая система => по определению есть
линейно зависимая система => по определению есть 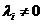
Рассмотрим систему, пусть все коэффициенты кроме 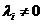 , равны нулю
, равны нулю 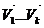 :
: 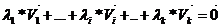
прибавим к этой системе  ; получим систему
; получим систему  , причем
, причем 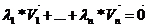 и
и 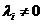 => по определению система
=> по определению система  является линейно зависимой.
является линейно зависимой.
2) пусть  является линейно независимой системой векторов, тогда любая её подсистема является линейно независимой.
является линейно независимой системой векторов, тогда любая её подсистема является линейно независимой.
Доказательство:
Предположим  содержит линейно зависимую систему векторов, тогда по первому свойству система
содержит линейно зависимую систему векторов, тогда по первому свойству система  будет линейно зависимой, это противоречит условию => предположение неверно => система
будет линейно зависимой, это противоречит условию => предположение неверно => система  не может содержать линейно зависимую подсистему => любая её подсистема является линейно независимой.
не может содержать линейно зависимую подсистему => любая её подсистема является линейно независимой.
3) если система векторов  содержит хотя бы один нулевой вектор, тогда система векторов
содержит хотя бы один нулевой вектор, тогда система векторов  является линейно зависимой.
является линейно зависимой.
Доказательство:
Рассмотрим такую линейную комбинацию: 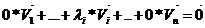 , причем
, причем 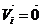 . Мы получили систему векторов
. Мы получили систему векторов  равную нулевому вектору с
равную нулевому вектору с 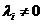 => система векторов
=> система векторов  линейно зависимая.
линейно зависимая.
4) пусть  линейно зависимая система векторов, тогда по крайне мере один вектор этой системы можно выразить через линейную комбинацию других векторов.
линейно зависимая система векторов, тогда по крайне мере один вектор этой системы можно выразить через линейную комбинацию других векторов.
Доказательство:
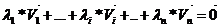
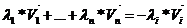
Т.к. система линейно зависимая, то существует i коэффициент не равный нулю (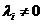 ), разделим на этот элемент правую и левую часть равенства.
), разделим на этот элемент правую и левую часть равенства.
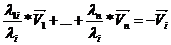
Линейная зависимость системы векторов, состоящей из одного вектора.
Система из одного вектора линейно зависима тогда и только тогда, когда 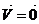 .
.
(=>) система векторов 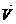 - линейно зависимая, Доказать
- линейно зависимая, Доказать 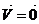
Доказательство:
По определению 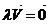 ,
, 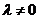 =>
=> 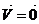
(<=) 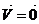 , доказать система векторов
, доказать система векторов 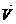 - линейно зависимая
- линейно зависимая
Доказательство:
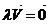 ,
, 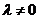 => система линейно зависимая.
=> система линейно зависимая.
Линейная зависимость системы векторов, состоящей из двух векторов.
Система векторов 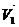 ,
,  линейно зависима тогда и только тогда, когда вектора параллельны между собой(
линейно зависима тогда и только тогда, когда вектора параллельны между собой(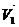 //
//  )
)
(=>) 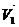 //
//  , доказать, что система линейно зависима.
, доказать, что система линейно зависима.
Доказательство:
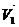 //
//  => по теореме о коллинеарных векторах
=> по теореме о коллинеарных векторах  =>
=> 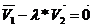 ,
, 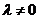 => система векторов
=> система векторов 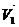 ,
,  линейно зависимая.
линейно зависимая.
(<=) Система векторов 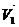 ,
,  линейно зависимая Доказать:
линейно зависимая Доказать: 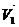 //
//  .
.
Доказательство:
Приложим начала векторов 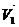 ,
,  к одной точке. Т.к система векторов линейно зависима, то
к одной точке. Т.к система векторов линейно зависима, то 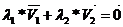 , причем
, причем 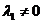 или
или  , пусть для определенности
, пусть для определенности 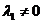 , тогда
, тогда  =>
=> 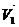 //
//  .
.
Линейная зависимость системы векторов, состоящей из трёх векторов.
Система векторов 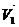 ,
,  ,
, 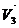 линейно зависима тогда и только тогда, когда вектора
линейно зависима тогда и только тогда, когда вектора 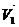 ,
,  ,
, 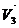 компланарны (если при приложение к одной точке начал векторов они лежат в одной плоскости, то такие вектора называются компланарными).
компланарны (если при приложение к одной точке начал векторов они лежат в одной плоскости, то такие вектора называются компланарными).
(<=)вектора 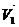 ,
,  ,
, 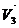 компланарные, Доказать: Система векторов
компланарные, Доказать: Система векторов 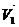 ,
,  ,
, 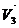 линейно зависима.
линейно зависима.
Доказательство:
1)если среди этих трех векторов, есть два параллельных между собой, то вся система векторов будет линейно зависимой(т.к. будет линейно зависимая подсистема).
2)приложим все вектора к одной точке. Рассмотрим в этой плоскости аффинную систему координат с базисом 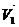 ,
,  .
.
=> 
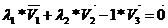
=> линейно зависима система векторов.
(=>)Система векторов 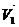 ,
,  ,
, 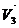 линейно зависима. Доказать
линейно зависима. Доказать 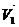 ,
,  ,
, 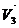 компланарные.
компланарные.
Доказательство:
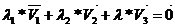 (
(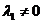 или
или  или
или 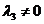 . пусть для определенности
. пусть для определенности 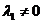 )
)
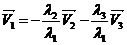
1)  //
// 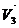 =>
=> 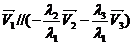 => компланарны.
=> компланарны.
2) вектора  ,
, 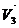 не коллинеарны. Приложим все 3 вектора к одной точке. Вектора
не коллинеарны. Приложим все 3 вектора к одной точке. Вектора  и
и 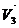 задают однозначно плоскость γ, рассмотрим аффинную систему координат с базисом
задают однозначно плоскость γ, рассмотрим аффинную систему координат с базисом  ,
, 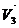 . Рассмотрим вектор с координатами
. Рассмотрим вектор с координатами 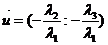 ,
, 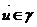 =>
=> 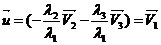 =>
=> 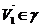 => вектора
=> вектора 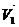 ,
,  ,
, 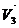 компланарные.
компланарные.
Замечание: Любая система из 4 векторов и более в 3 мерном пространстве линейно зависимая.
Деление отрезка в заданном отношение.
 Рассмотрим прямую n,
Рассмотрим прямую n,  , АВ – отрезок.
, АВ – отрезок.
Рассмотрим на n точку С(xC, yC); 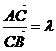 . Будем говорить С делит АВ в отношение λ.
. Будем говорить С делит АВ в отношение λ.
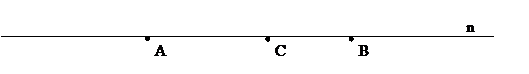 1) Пусть точка С лежит на отрезке АВ.
1) Пусть точка С лежит на отрезке АВ.
λ>0
 2) Пусть точка С лежит правее точки В.
2) Пусть точка С лежит правее точки В.
λ>0 |λ|>1
 3) Пусть точка С лежит левее точки А.
3) Пусть точка С лежит левее точки А.
λ>0 |λ|<1
найдем координаты точки С.
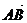 (xb-xa;yb-ya),
(xb-xa;yb-ya), 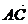 (xa-xc,ya-yc),
(xa-xc,ya-yc), 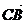 (xc-xb,yc-yb)
(xc-xb,yc-yb)
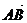 =
= 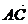 +
+ 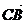 ,
, 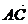 =λ*
=λ* 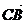 =>
=> 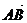 =
= 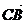 (λ+1)
(λ+1)
xb-xa=xb*(1+ λ)
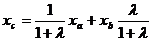 (аналогично для yc,zc).
(аналогично для yc,zc).
Деление отрезка в отношение.
Пусть точка С делит отрезок АВ в отношение λ, тогда 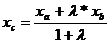 (аналогично для yc и zc).
(аналогично для yc и zc).
Доказательство: формула деления отрезка в определенном отношение.
Следствие: пусть С середина отрезка АВ, тогда xc=(xa+xb)/2.
Направляющие косинусы.
Пусть в трёхмерном пространстве есть прямоугольная система координат XYZ.

Обозначим через α угол между вектором 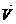 и лучом ОХ, через β угол между вектором
и лучом ОХ, через β угол между вектором 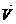 и лучом ОY, через γ угол между вектором
и лучом ОY, через γ угол между вектором 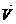 и лучом ОZ.
и лучом ОZ.
Определение: cos α, cos β, cos γ – направляющие косинусы вектора 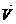 .
.
Теорема:  .
.
Доказательство: проведем через конец вектора 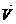 :
:
- прямую перпендикулярную ОХ, эта прямая пересекает ОХ в точки А.
- прямую перпендикулярную ОY, эта прямая пересекает ОY в точки B.
- прямую перпендикулярную ОZ, эта прямая пересекает ОХ в точки C.



Проведем через конец вектора 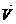 прямую перпендикулярную плоскости (XOY), эта прямая пересекает плоскость (XOY) в точке D, через точку D проведем прямую перпендикулярную ОХ и так далее будем проводить прямые перпендикулярные к осям.
прямую перпендикулярную плоскости (XOY), эта прямая пересекает плоскость (XOY) в точке D, через точку D проведем прямую перпендикулярную ОХ и так далее будем проводить прямые перпендикулярные к осям.
 ,
,  =>
=> 
 =>
=>  .
.



 ,
, 
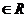 , тогда выражение вида
, тогда выражение вида 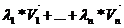 называется линейной комбинацией векторов
называется линейной комбинацией векторов 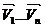 , линейная комбинация называется тривиальной, если
, линейная комбинация называется тривиальной, если 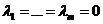 (тривиальная комбинация векторов =
(тривиальная комбинация векторов =  ).
).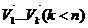 , тогда система
, тогда система 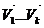 линейно зависимая система => по определению есть
линейно зависимая система => по определению есть 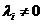
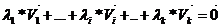
 ; получим систему
; получим систему 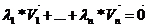 и
и 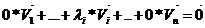 , причем
, причем 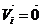 . Мы получили систему векторов
. Мы получили систему векторов 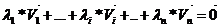
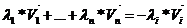
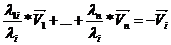
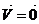 .
.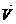 - линейно зависимая, Доказать
- линейно зависимая, Доказать 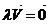 ,
, 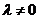 =>
=> 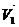 ,
,  линейно зависима тогда и только тогда, когда вектора параллельны между собой(
линейно зависима тогда и только тогда, когда вектора параллельны между собой( =>
=> 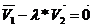 ,
, 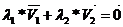 , причем
, причем 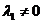 или
или  , пусть для определенности
, пусть для определенности  =>
=> 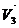 линейно зависима тогда и только тогда, когда вектора
линейно зависима тогда и только тогда, когда вектора 
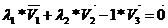
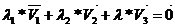 (
(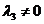 . пусть для определенности
. пусть для определенности 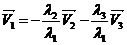
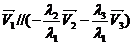 => компланарны.
=> компланарны.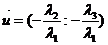 ,
, 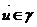 =>
=> 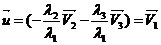 =>
=> 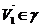 => вектора
=> вектора  Рассмотрим прямую n,
Рассмотрим прямую n,  , АВ – отрезок.
, АВ – отрезок.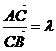 . Будем говорить С делит АВ в отношение λ.
. Будем говорить С делит АВ в отношение λ.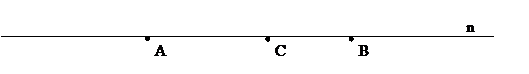 1) Пусть точка С лежит на отрезке АВ.
1) Пусть точка С лежит на отрезке АВ. 2) Пусть точка С лежит правее точки В.
2) Пусть точка С лежит правее точки В. 3) Пусть точка С лежит левее точки А.
3) Пусть точка С лежит левее точки А.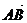 (xb-xa;yb-ya),
(xb-xa;yb-ya), 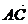 (xa-xc,ya-yc),
(xa-xc,ya-yc), 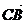 (xc-xb,yc-yb)
(xc-xb,yc-yb)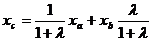 (аналогично для yc,zc).
(аналогично для yc,zc).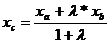 (аналогично для yc и zc).
(аналогично для yc и zc).
 .
.


 ,
,  =>
=> 
 =>
=> 


