ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Общий вид дифференциального уравнения следующий:
F (x, y, y /, y //,…, y ( n )) = 0.
Здесь x – независимая переменная, y – искомая функция, n – наивысший порядок производной, с которым искомая функция входит в уравнение. Значение n называется порядком дифференциального уравнения.
Часто имеют дело с уравнениями, разрешенными относительно производной. Например, уравнение 2-го порядка, разрешенное относительно старшей производной, имеет вид
y // = f (x, y, y / ).
Решением дифференциального уравнения в интервале (a, b) называется функция y = y (x), обращающее это уравнение в тождество по переменной x.
Простейшим дифференциальным уравнением является уравнение y / = f (x), решениями которого, очевидно, являются все первообразные функции f (x):
y = F (x) + C, где С – произвольная постоянная. Таким образом, задача интегрирования есть частный случай задачи решения дифференциального уравнения.
Как правило, решение дифференциального уравнения n -го порядка определяются с точностью до n произвольных постоянных. Например, решениями дифференциального вида
y/// = 2 x + 1
являются функции y (x, C1, C2, C3) =  + C1
+ C1 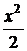 + C2 x + C3.
+ C2 x + C3.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Общий вид дифференциального уравнения первого порядка следующий:
F (x, y, y /) = 0. (1)
Здесь x – независимая переменная, y – искомая функция
Дифференциальные уравнения первого порядка, разрешенные относительно производной, имеют общий вид
= f (x, y). (2)
Пусть ставится задача: найти решение уравнения (2), удовлетворяющее условию y (x 0) = y 0. Эта задача называется задачей Коши с начальными значениями (x 0, y 0).
Теорема существования и единственности. Для того, чтобы задача Коши имела единственное решение в некоторой области G начальных значений (x 0, y 0) достаточно, чтобы функция f (x, y) была непрерывна в области Gвместе с f y / (x, y).
График решения
y =
y (
x)дифференциального уравнения называют
интегральной кривой. Теорема утверждает, что через каждую точку области G, в которой непрерывны
f (
x,
y) и
fy /(
x,
y), проходит, и притом единственная, интегральная кривая (рис.1).
рис.1
Линейные уравнения
Линейными дифференциальными уравнениями первого порядка называются уравнения вида y / + a (x) y = b (x), где a (x), b (x)– непрерывные функции. Если b (x)=0, то в этом случае линейное уравнение называют однородным. Линейное однородное уравнение является уравнением с разделяющимися переменными. Решаем его.
Из y / + a (x) y = 0 следует = – a (x) dx, откудаln | y | = –ò a (x) dx + ln |С|, C¹0. Поскольку y = 0 – специальное (тривиальное) решение, то общее решение линейного однородного уравнения записывается в виде
y одн =C×exp(–ò a (x) dx), C – произвольная постоянная (8)
(exp(x) – часто используемое в литературе обозначение функции ex). Для решения неоднородного уравнения применяют метод вариации произвольной постоянной. Вкратце опишем его. Согласно этому методу постоянная C заменяется функцией C=C(x), т.е. превращается в переменную величину, иначе говоря, варьируется. Выражение y = C(x)×exp(–ò a (x) dx)подставляем в неоднородное уравнение, получается дифференциальное уравнение уже относительно функции C(x), которая затем находится, и при этом появляется другая постоянная. Таким образом получится общее решение неоднородного уравнения. Рассмотрим примеры.
Пример. Решить уравнение y / – y = (x +1)3.
Решение. Соответствующее однородное уравнение имеет вид y / – y =0. Здесь a (x) = –. Получаем согласно (8)
y одн =C×exp(ò dx) = C×exp(2×ln | x +1|) = C(x +1)2.
ВарьируемC: C=C(x).Подставляем y = C(x +1)2 в исходное уравнение:
(x +1)2 + 2C(x +1) – C(x +1)2 = (x +1)2 = (x +1)3,
откуда = x +1иC(x) = (x +1)2 + D. Теперь можно записать общее решение исходного неоднородного линейного дифференциального уравнения с новой произвольной постоянной D: y = C(x)×(x +1)2 = (x +1)4 + D(x +1)2.
Пример. Решить уравнение 2 x (x 2 + y) dx = dy.
Решение. Данное уравнение преобразуется к виду – 2 xy = 2 x 3. Здесь
a (x)= –2 x и соответствующее однородное уравнение y /– 2 xy = 0. Его общее решение y одн =C×exp(ò 2 xdx) = C×exp(x 2). Полагая C = C(x) и подставляя C в исходное уравнение y / – 2 xy = 2 x 3, получаем
exp(x 2) + 2C x ×exp(x 2) – 2 x ×C×exp(x 2) = 2 x 3 или = 2 x 3×exp(– x 2).
Определяем C(x);с этой целью используем замену t = x 2, dt = 2 x dx, а затем интегрирование по частям:
C(x) = ò 2 x 3×exp(– x 2) dx = ò t ×exp(– t) dt = – t ×exp(– t) + ò exp(– t) dt =
= – (t +1)×exp(– t) + D = – (x 2 + 1) ×exp(– x 2) + D.
Здесь D – новая произвольная постоянная. Получаем общее решение исходного уравнения в виде y = C(x)×exp(x 2) = D×exp(x 2) – x 2 – 1.
Уравнение Бернулли
Уравнения Бернулли имеют вид y / + a (x) y = b (x)× yn. Если n =1, то имеем однородное линейное дифференциальное уравнение. При n¹ 1 уравнение Бернулли приводится к линейному уравнению делением обеих частей на yn и последующей заменой z = y 1 – n.
Пример. Решить уравнение x × y / – 2 x 2 = 4 y.
Решение. Преобразуем данное уравнение, после чего будет видно, что имеем дело с уравнением Бернулли. Действительно,
y / – 2 x = 4 или y / – 4 = 2 x = 2 xy 1/2.
Здесь a (x) = –, b (x) = 2 x, n = 1/2. Имея в виду, что y = 0 – специальное решение, делим на y 1/2 и получаем преобразованное уравнение – 4 = 2 x. Теперь делаем замену
z = y 1 – 1/2 = y 1/2, z¢ = y –1/ 2× y¢ = и 2 z ¢ =,
откуда получаем линейное дифференциальное уравнение относительно функции z (x): 2 z¢ – 4 =2 x или z¢ – 2 = x. Решим его. Запишем соответствующее однородное уравнение z¢ – 2 =0, его общим решением будет
z одн = С×exp(ò dx) = С×exp(2ln | x |) = C x 2.
Применяя метод вариации произвольной постоянной получаем
C¢ x 2 + 2C x – 2 = C¢ x 2 = x или C¢=1/ x,
откуда C(x) = ln | x | + D, z (x)=C(x)× x 2 = (ln | x | + D)× x 2. Т.к. = z, то общее решение данного уравнения Бернулли имеет вид y = (ln | x | + D)2× x 4, а также есть специальное решение y =0.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Общий вид дифференциального уравнения следующий:
F (x, y, y /, y //,…, y ( n )) = 0.
Здесь x – независимая переменная, y – искомая функция, n – наивысший порядок производной, с которым искомая функция входит в уравнение. Значение n называется порядком дифференциального уравнения.
Часто имеют дело с уравнениями, разрешенными относительно производной. Например, уравнение 2-го порядка, разрешенное относительно старшей производной, имеет вид
y // = f (x, y, y / ).
Решением дифференциального уравнения в интервале (a, b) называется функция y = y (x), обращающее это уравнение в тождество по переменной x.
Простейшим дифференциальным уравнением является уравнение y / = f (x), решениями которого, очевидно, являются все первообразные функции f (x):
y = F (x) + C, где С – произвольная постоянная. Таким образом, задача интегрирования есть частный случай задачи решения дифференциального уравнения.
Как правило, решение дифференциального уравнения n -го порядка определяются с точностью до n произвольных постоянных. Например, решениями дифференциального вида
y/// = 2 x + 1
являются функции y (x, C1, C2, C3) =  + C1
+ C1 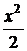 + C2 x + C3.
+ C2 x + C3.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Общий вид дифференциального уравнения первого порядка следующий:
F (x, y, y /) = 0. (1)
Здесь x – независимая переменная, y – искомая функция
Дифференциальные уравнения первого порядка, разрешенные относительно производной, имеют общий вид
= f (x, y). (2)
Пусть ставится задача: найти решение уравнения (2), удовлетворяющее условию y (x 0) = y 0. Эта задача называется задачей Коши с начальными значениями (x 0, y 0).
Теорема существования и единственности. Для того, чтобы задача Коши имела единственное решение в некоторой области G начальных значений (x 0, y 0) достаточно, чтобы функция f (x, y) была непрерывна в области Gвместе с f y / (x, y).
График решения
y =
y (
x)дифференциального уравнения называют
интегральной кривой. Теорема утверждает, что через каждую точку области G, в которой непрерывны
f (
x,
y) и
fy /(
x,
y), проходит, и притом единственная, интегральная кривая (рис.1).
рис.1



 + C1
+ C1 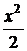 + C2 x + C3.
+ C2 x + C3.



