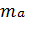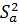Рассмотрим теперь методы интервального оценивания.
Доверительным интервалом называется интервал (a; b), в который с задан-
ной вероятностью р попадает оцениваемый параметр.
Вероятност ь р называется доверительной. Вместо нее часто задают величину  =1- p, называемую уровнем значимости. Если выборка объема п представляет случайную величину, распределенную нормально, то
=1- p, называемую уровнем значимости. Если выборка объема п представляет случайную величину, распределенную нормально, то
доверительный интервалы для матожидания:

Для дисперсии:

где 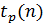 и
и  - квантили распределения Стьюдента и хи-квадрат,
- квантили распределения Стьюдента и хи-квадрат,
 =1- p.
=1- p.
Электронная таблица Excel (Calc), содержащая встроенные статистические функции позволяет легко и быстро найти доверительные интервалы для математического ожидания и дисперсии. Рассмотрим решение этой задачи.
Возвращаемся на лист 1 электронной таблицы с данными
примера и для них вычислим доверительные интервалы при р =0,95.
Вводим данные согласно рисунку:

Для вычисления величины 
служит функция «ДОВЕРИТ»(«CONFIDENCE») категории «Статистические» с тремя параметрами «Альфа» - уровень значимости
 =1- p, «Станд_откл» - среднеквадратическое отклонение S,
=1- p, «Станд_откл» - среднеквадратическое отклонение S,
«Размер» - объем выборки п.
Таким образом, вводим в Н3 функцию:
=СРЗНАЧ(А1:А25)-ДОВЕРИТ(I1;СТАНДОТКЛОН(А1:А25);25)
(=AVERAGE(A1:A25)-CONFIDENCE(I1;CTDEV(A1:A25);25))
а в ячейку I3 функцию:
=СРЗНАЧ(А1:А25)+ДОВЕРИТ(I1;СТАНДОТКЛОН(А1:А25);25)
(=AVERAGE(A1:A25)+CONFIDENCE(I1;CTDEV(A1:A25);25))
Для вычисления доверительного интервала для дисперсии следует от-
метить, что функция вычисления квантили распределения хи-квадрат
(обратного распределения хи-квадрат) называется «ХИ2ОБР» («СHIINV»)
(категория «Статистические») и имеет два параметра:
первый «Вероятность» содержит доверительную вероятность р,
второй – степень свободы п -1.
Вводим в соответствии с данными условиями и формулой для довери-
тельного интервала в ячейку Н4 запись:
=ДИСП(A1:A25)*24/ХИ2ОБР(0,025;24)
(=VAR(A1:A25)*24/CHIINV(0,025;24))
а в ячейку I4 запись:
=ДИСП(A1:A25)*24/ХИ2ОБР(0,975;24)
(=VAR(A1:A25)*24/CHIINV(0,975;24))
.
Получаем значения границ доверительных интервалов.
Задание 2. Для данных из задания 4 лабораторной работы № 1
вычислить доверительные интервалы для матожидания и дисперсии
при  = 0,01. Изменяя значение уровня значимости
= 0,01. Изменяя значение уровня значимости 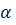 сделать вывод о
сделать вывод о
его влиянии на ширину интервала.
Лабораторная работа№ 3
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
О ВИДЕ РАСПРЕДЕЛЕНИЯ
Цель: Ознакомиться с методами проверки статистических гипотез о принадлежности генеральной совокупности, представленной выборочными данными, к тому или иному типу распределений, используя критерий согласия Пирсона (хи-квадрат) с помощью Excel(Calc).
Методы проверки статистических гипотез занимают центральное место в исследованиях математической статистики. Одной из важнейших групп критериев проверки статистических гипотез являются критерии
проверки гипотез о виде распределений (критерии согласия). Они по
выборочным данным проверяют предположение о принадлежности
генеральной совокупности к тому или иному виду распределений. Одним из наиболее мощных критериев согласия является критерий Пирсона, называемый еще критерием хи-квадрат. Его суть заключается в
сравнении теоретических частот элементов выборки ni (для дискретных распределений) с теоретическими частотами ni ′ = npi, где pi - вероятность принять это значение, рассчитанное по исследуемому закону распределения. Если распределение непрерывное, то строится группированный статистический ряд из k интервалов и pi = F (bi) - F (ai ) есть вероятность попасть в i -й интервал группировки (здесь F (x) - функция распределения проверяемого закона функция Лапласа).
Статистикой критерия является величина  .
.
Критическое значение критерия равно обратному распределению хи-квадрат со степенями свободы (k-r -1):  , где r – число оцениваемых параметров закона распределения.
, где r – число оцениваемых параметров закона распределения.
Распределение можно считать соответствующим теоретическому, если выполняется условие 
 .
.
Рассмотрим решение данной задачи на примере.
ПРИМЕР 1. Имеется выборка измерения пульса у 40 больных, подвергнутых некоторой лечебной процедуре. Проверить гипотезу о том, что значение пульса у подобных больных распределено по нормальному закону распределения. Взять уровень значимости α= 0,05.
Выборка ЧСС у 40 больных (уд/мин).
64 56 69 78 78 83 47 65 77 57 61 52 50 58 60 48 62 63 68 64
64 64 79 66 65 62 85 75 88 61 82 52 72 75 84 66 62 73 64 74
Для проверки гипотезы о принадлежности генеральной совокупности нормальному виду распределений необходимо строить группированный статистический ряд, т.к. нормальное распределение является непрерывным. Для этого нужно знать размах выборки, который равен разнице между максимальным и минимальным элементами выборки. Кроме того, нужно рассчитать точечные оценки математического ожидания и среднеквадратического отклонения (СКО). Открываем электронную таблицу и вводим данные выборки в ячейки А2-А41, делаем подписи для расчетных параметров в соответствии с рисунком:
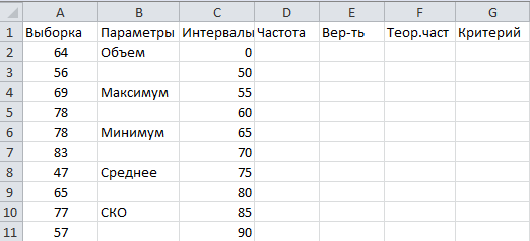
Вычисляем параметры по выборке. Для этого вводим в ячейку В3: «=СЧЁТ(A2:A41) (=COUNT(A2:A41))»
(здесь и далее кавычки вводить не надо, функции можно вводить с помощью мастера функций из категории «Статистические», как в лабораторной работе № 2, ссылки на ячейки можно ввести щелкнув мышью по ячейке).
В В5 вводим: «=МАКС(A2:A41)( =MAX(A2:A41))»,
в В7: «=МИН(A2:A41)( =MIN(A2:A41))»,
в В9: «=СРЗНАЧ(A2:A41)( =AVERAGE(A2:A41))»,
в В11: «=СТАНДОТКЛОН(A2:A41)( =STDEV(A2:A41))».
Видно, что весь диапазон значений элементов лежит на интервале от 47
до 88. Разобьем этот интервал на интервалы группировки:
[0; 50], (50; 55], (55; 60], (60; 65], (65; 70], (70; 75], (75; 80], (80; 85], (85; 90]. Для этого вводим в ячейки С2-С11 границы интервалов:
| ячейка
| С2
| С3
| С4
| С5
| С6
| С7
| С8
| С9
| С10
| С11
|
| число
|
|
|
|
|
|
|
|
|
|
|
Для вычисления частот пi используем функцию ЧАСТОТА
(FREQUENCY из категории «массив»).
Для этого в D3 вводим формулу
«=ЧАСТОТА(A2:A41;C3:C11) (FREQUENCY(A2:A41;C3:C11))».
В Calc значения частот появятcя сразу для всех интервалов.
В Excel: обводим курсором ячейки D3-D11, выделяя их и нажимаем F2, а затем одновременно Ctrl+Shift+Enter. В результате в ячейках D3-D11 окажутся значения частот.
Для расчета теоретической вероятности pi = F(bi) - F(ai)
вводим в ячейку Е3 разницу между функциями нормального распределения (функция НОРМРАСП (NORMDIST) категории «Статистические»
с параметрами:
«Х» – значение границы интервала, «Среднее» - ссылка на ячейкуВ9, «Стандартное_откл» - ссылка на В11, «Интегральная» - 1.
В результате в Е3 будет формула:
=НОРМРАСП(C3;$B$9;$B$11;1)-НОРМРАСП(C2;$B$9;$B$11;1)
( =NORMDIST(C3;B9;B11;1)-NORMDIST(C2;B9;B11;1))
Автозаполняем эту формулу на Е3-Е10, перемещая нижний правый
угол Е3 до ячейки Е10.
В последней ячейке столбца Е11 для соблюдения условия нормировки вводим дополнение предыдущих вероятностей до единицы. Для этого вводим в Е11: «=1-СУММ(E3:E10)» (можно без нормировки)
Для расчета теоретической частоты ni′ = npi вводим в F3 формулу: «=E3*$B$3», автозаполняем ее на F3-F11.
Для вычисления элементов суммы  критерия Пирсона
критерия Пирсона
вводим в G3 значение «=(D3-F3)*(D3-F3)/F3» и автозаполняем его на
диапазон G3-G11.
Находим значение критерия  и критическое значение
и критическое значение 
Для этого вводим в F12 подпись «Сумма», а в F13 подпись «Критич.».
Вводим в соседние ячейки формулы –
в G12: «=СУММ(G3:G11) (=SUM(G3:G11))»,
а в G13: «=ХИ2ОБР(0,05;6) (=CHIINV(0,05;6))»,
здесь параметр a = 0,05 взят из условия, а степень свободы (k-r-1)=(9-2-1)=6, так как k=9 – число интервалов группировки, а r=2, т.к. были оценены два параметра нормального распределения: математическое ожидание и СКО.
Видно, что 
 ,
,
то есть можно считать, что ЧСС у данной группы больных распределена по нормальному закону распределения.
Наглядно увидеть это можно, построив графики плотностей эмпирического и теоретического распределений.
Ставим курсор в любую свободную ячейку и вызываем мастер диаграмм (Вставка/Диаграмма). Выбираем тип диаграммы «График» и вид «График с маркерами» самый левый во второй строке, нажимаем «Далее».
Ставим курсор в поле «Диапазон» и удерживая кнопку CTRL обводим мышью область ячеек D3-D11 а затем F3-F11. Переходим на закладку «Ряд» и в поле «Подписи оси Х» обводим область С3-С11. Нажимаем «Готово». Видно, что графики достаточно хорошо совпадают, что говорит о соответствии данных нормальному закону.
Задание 1. Для данных из задания 4 лабораторной работы № 1
Проверить по критерию Пирсона на уровне значимости α = 0,02 статистическую гипотезу о том, что генеральная совокупность, представленная выборкой, имеет нормальный закон распределения.
Лабораторная работа № 4
ОСНОВЫ РЕГРЕССИОННОГО И
КОРРЕЛЯЦИОННОГО АНАЛИЗА
Цель: Освоить методы построения линейного уравнения парной регрессии, научиться получать и анализировать основные характеристики регрессионного уравнения.
Уравнение регрессии строится для анализа статистических зависимостей между двумя или более показателями. Если показателей два, то регрессия называется парной. Если зависимость между показателями Х и Y пропорциональная, то регрессия будет линейной и описывается уравнением вида y = ax + b. Рассмотрим методику построения регрессионного уравнения на примере анализа веса щитовидной железы (Y) и соответствующей площади ее скенографического изображения (X).
ПРИМЕР.
Введем эту таблицу в ячейки А1-M2 электронной книги Excel.
Просмотрим предварительно, как лежат точки на графике и какое уравнение регрессии лучше выбрать. Для этого строим график.
Вызвав мастер диаграмм, выбираем тип диаграммы «Точечная», нажимаем «Далее» и, поместив курсор в поле «Диапазон» обводим курсором данные Y (ячейки В2-М2). Переходим на закладку «Ряд» и в поле «Значения Х»
делаем ссылку на ячейки В1-М1, обводя их курсором. Нажимаем «Готово».
Как видно из графика, точки хорошо укладываются на прямую линию, поэтому будем находить уравнение линейной регрессии вида y = ax + b.
Для нахождения коэффициентов а и b уравнения регрессии
служат функции НАКЛОН (SLOPE) и ОТРЕЗОК (INTERCEPT) категории «Статистические».
Вводим в А5 подпись «а=» а в соседнюю ячейку В5 вводим функцию
НАКЛОН (SLOPE), ставим курсор в поле «Изв_знач_у» задаем ссылку на ячейки В2-М2, обводя их мышью. Аналогично в поле «Изв_знач_х» даем
ссылку на В1-М1. Результат 3,36. Найдем теперь коэффициент b.
Вводим в А6 подпись «b=», а в В6 функцию ОТРЕЗОК (INTERCEPT) с теми же параметрами, что и у функции НАКЛОН (SLOPE),. Результат - 42,6.
Следовательно, уравнение линейной регрессии есть y = 3,33x - 42,6.
Построим график уравнения регрессии. Для этого в третью строчку таблицы введем значения функции регрессии в заданных точках Х (первая строка) –  . Для получения этих значений используется функция ТЕНДЕНЦИЯ (FORECAST) категории «Статистические». Вводим в
. Для получения этих значений используется функция ТЕНДЕНЦИЯ (FORECAST) категории «Статистические». Вводим в
А3 подпись «Y(X)» и, поместив курсор в В3, вызываем функцию
ТЕНДЕНЦИЯ (FORECAST).
Для Excel: в полях «Изв_знач_у» и «Изв_знач_х» даем ссылку на В2-М2 и В1-М1. В поле «Нов_знач_х» вводим также ссылку на В1-М1. В поле «Константа» вводят 1, если уравнение регрессии имеет вид y = ax + b, и 0, если y = ax. В нашем случае вводим единицу. Функция ТЕНДЕНЦИЯ является массивом, поэтому для вывода всех ее значений выделяем область В3-М3 и нажимаем F2 и Ctrl+Shift+Enter. Результат – значения уравнения регрессии в заданных точках.
В Calc: в поле «Значение» вводим массив В1-М1, в поле «Данные Y» - ссылку на В2-М2, в поле «Данные X» -ссылку на В1-М1. В поле «Массив» поставим флажок, нажимаем ОК и массив B3:M3 заполнится значениями, вычисленными по линейной регрессии.
Строим график. Ставим курсор в любую свободную клетку, вызываем мастер диаграмм, выбираем категорию «Точечная», вид графика – линия без
точек, нажимаем «Далее», в поле «Диапазон» вводим ссылку на В3-М3. Переходим на закладку «Ряд» и в поле «Значения Х» вводим ссылку на В1-М1, нажимаем «Готово». Результат – прямая линия регрессии.
Посмотрим, как различаются графики опытных данных и уравнения регрессии. Для этого ставим курсор в любую свободную ячейку, вызываем мастер диаграмм, категория «График», вид графика – ломаная линия с точками (или точечная с прямыми отрезками), нажимаем «Далее», в поле «Диапазон» вводим ссылку на вторую и третью строки В2-М3. Переходим на закладку «Ряд» и в поле «Подписи оси Х» вводим ссылку на В1-М1, нажимаем «Готово». Результат – две линии (Синяя – исходные данные, красная – уравнение регрессии). Видно, что линии мало различаются между собой.
Линия регрессии позволяет с некоторой вероятностью предсказать в интервале от X=11 до X=89 любые значения функции Y при отсутствущих значениях фактора X, но и за пределами данного интервала. Так, например, чтобы вычислить вес щитовидной железы, соответствующий площади скеннографического изображения равной Х=90 см3, воспользуемся встроенной статитическиой функцией ПРЕДСКАЗ. Расчет показывает, что вес щитовидной железы будет в этом случае равен Y=259,64.
Для вычисления коэффициента корреляции  служит функция КОРРЕЛ. Размещаем графики так, чтобы они располагались выше
служит функция КОРРЕЛ. Размещаем графики так, чтобы они располагались выше
25 строки, и в А25 делаем подпись «Корреляция», в В25 вызываем
функцию Коррел, в полях которой «Массив 1» и «Массив 2» вводим
ссылки на исходные данные В1-М1 и В2-М2. Результат 0,9951.
Коэффициент детерминации Rxy – это квадрат коэффициента корреляции  . В А26 делаем подпись «Детерминация», а в В26 – формулу «=В25*В25». Результат 0,98, т.е. 98% всех изменений одного признака связано с изменением другого.
. В А26 делаем подпись «Детерминация», а в В26 – формулу «=В25*В25». Результат 0,98, т.е. 98% всех изменений одного признака связано с изменением другого.
Однако, в Excel существует одна функция, которая рассчитывает
все основные характеристики линейной регрессии. Это функция ЛИНЕЙН. Ставим курсор в В28 и вызываем функцию ЛИНЕЙН, категории «Статистические».
В полях «Изв_знач_у» и «Изв_знач_х» даем ссылку на В2-М2 и В1-М1.
Поле «Константа» имеет тот же смысл, что и в функции ТЕНДЕНЦИЯ, у нас она равна 1. Поле «Стат» должно содержать 1, если нужно вывести полную статистику о регрессии. В нашем случае ставим туда единицу. Функция возвращает массив размером 2 столбца и 5 строк. После ввода выделяем мышью ячейки В28- С32 и нажимаем F2 и Ctrl+Shift+Enter. Результат – таблица значений, числа в которой имеют следующий смысл:
| Коэффициент а
| Коэффициент b
|
Стандартная ошибка 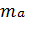
| Стандартная ошибка 
|
| Коэффициент детерминации Rxy
| Среднеквадратическое отклонение y
|
| F – статистика
| Степери свободы n-2
|
Регрессионная сумма квадратов 
| Остаточная сумма квадратов 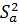
|
Анализ результата:
в первой строчке – коэффициенты уравнения регрессии, сравните их с рассчитанными функциями НАКЛОН и ОТРЕЗОК.
Вторая строчка – стандартные ошибки коэффициентов.
Если одна из них по модулю больше чем сам коэффициент, то коэффициент считается нулевым. Коэффициент детерминации характеризует качество связи между факторами. Полученное значение 0,9902 говорит об очень хорошей связи факторов. F – статистика проверяет гипотезу об адекватности регрессионной модели.
Данное число нужно сравнить с критическим значением. Для его получения вводим в Е33 подпись «F-критическое», а в F33 функцию FРАСПОБР, аргументами которой вводим соответственно «0,05» (уровень значимости), «1»(число факторов Х) и «10» (степени свободы). Видно, что F – статистика больше, чем F– критическое, значит регрессионная модель адекватна.
В последней строке приведены регрессионная сумма квадратов и остаточные суммы квадратов. Важно, чтобы регрессионная сумма (объясненная регрессией) намного больше остаточной (не объясненная регрессией, вызванная случайными факторами). В нашем случае это условие выполняется, что говорит о хорошей регрессии.
Задание. Даны выборки факторов xi и yi. По этим выборкам:
1) Построить эмпирическую линию регрессии (ломаную линию).
2) Найти уравнение линейной регрессии.
3) Найти коэффициент парной корреляции, коэффициент детерминации.
4) Проверить на уровне значимости a = 0,05 регрессионную модель на адекватность.
Вариант 1, 7
| Средняя длина тела плода (см)
|
|
|
|
|
|
|
|
|
|
| Возраст внутри утробного плода(нед)
|
|
|
|
|
|
|
|
|
|
Вариант2, 8
| Площадь поражения артерии таза (%)
| 22,3
| 3,1
| 48,3
|
| 7,5
| 40,2
| 23,1
|
| 32,5
|
|
| Возраст (в годах)
|
|
|
|
|
|
|
|
|
|
|
Вариант 3, 9
| Содержание андростерона в моче(мг/в сут)
| 0,82
| 0,9
| 0,98
| 1,06
| 1,2
| 1,29
| 1,48
| 1,42
| 1,4
| 1,08
|
| Возраст (в годах)
|
|
|
|
|
|
|
|
|
|
|
Вариант 4, 10
| Концентрация пролактина в крови (нг/мл)
|
|
|
|
|
|
|
|
|
|
|
| Возраст (в годах)
|
|
|
|
|
|
|
|
|
|
|
Вариант 5, 11
| Поверхность тела (м2)
| 1,1
| 1,5
| 1,2
| 1,3
| 1,9
| 1,3
|
| 1,7
| 1,5
| 1,7
|
| Вес(кг)
|
|
|
|
|
|
|
|
|
|
|
Вариант 6, 12
| Объем циркулирующей крови (л)
| 4,83
| 5,08
| 3,81
| 5,34
| 4,06
| 5,34
| 4,32
| 5,59
| 4,57
| 5,8
|
| Рост (см)
|
|
|
|
|
|
|
|
|
|
|
Замечание: При решении задачи выборку (Xi;Yi) целесообразно занести в электронную таблицу по возрастанию фактора Xi.



 =1- p, называемую уровнем значимости. Если выборка объема п представляет случайную величину, распределенную нормально, то
=1- p, называемую уровнем значимости. Если выборка объема п представляет случайную величину, распределенную нормально, то

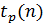 и
и  - квантили распределения Стьюдента и хи-квадрат,
- квантили распределения Стьюдента и хи-квадрат,
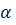 сделать вывод о
сделать вывод о .
. , где r – число оцениваемых параметров закона распределения.
, где r – число оцениваемых параметров закона распределения.
 .
.
 критерия Пирсона
критерия Пирсона и критическое значение
и критическое значение 
 . Для получения этих значений используется функция ТЕНДЕНЦИЯ (FORECAST) категории «Статистические». Вводим в
. Для получения этих значений используется функция ТЕНДЕНЦИЯ (FORECAST) категории «Статистические». Вводим в служит функция КОРРЕЛ. Размещаем графики так, чтобы они располагались выше
служит функция КОРРЕЛ. Размещаем графики так, чтобы они располагались выше