Самаров- ТЕОРИЯ ВЕРОЯТНОСТЕЙ.pdf - стр. 7-9
+
См. лекция 5 по Теория вероятности (Борисов).
См. лекция 6 Теория вероятности (Борисов). (ОСНОВНЫЕ ТЕОРЕМЫ О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ И ДИСПЕРСИИ.)
11. Важнейшие виды распределений дискретных случайных величин (геометрическое, биномиальное, Пуассона) и их характеристики.
Самаров- ТЕОРИЯ ВЕРОЯТНОСТЕЙ.pdf - стр. 9-10
+
См. Теория вероятности (Борисов). ЛЕКЦИЯ 5.pdf
+
Геометрическое распределение.
Дискретная случайная величина X имеет геометрическое распределение, если она принимает значения 1, 2,..., m,... (бесконечное, но счётное множество значений) с вероятностями
P(X=m)=pqm-1, где 0<p<1, q=1-p, m=1, 2,...
Ряд геометрического распределения имеет вид:
Очевидно, что вероятности pi образуют геометрическую прогрессию с первым членом p и знаменателем q (отсюда и название "геометрическое распределение"). Определение геометрического распределения корректно, так как сумма ряда:
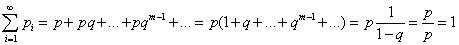
Случайная величина X=m, имеющая геометрическое распределение, представляет собой число m испытаний, проведённых по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.
Математическое ожидание случайной величины X, имеющей геометрическое распределение с параметром p:
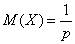
Дисперсия
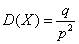 , где q=1-p.
, где q=1-p.
Пример. Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.
Решение. Случайная величина X - число сделанных выстрелов - имеет геометрическое распределение с параметром p=0,6. Ряд распределения X имеет вид:
xi 1 2 3... m...
pi 0,6 0,24 0,096... 0,6·0,4m...
По формулам:
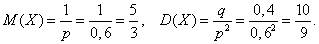
Вероятность того, что для поражения цели потребуется не более трёх патронов равна
P(X≤3)=P(X=1)+P(X=2)+P(X=3)=0,6+0,24+0,096=0,936.
Биномиальное распределение.
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, распределение Бернулли, - распределение вероятностей случайной величины X, принимающей целочисленные значения х = 0, 1,..., n с вероятностями соответственно.
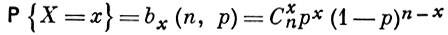
(Сxn - биномиальный коэффициент; р - параметр Б. р., наз. вероятностью положительного исхода, принимающей значения на отрезке 0 ≤ р ≤ 1). Б. р. - одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Пусть Y1, Y2,... - последовательность независимых случайных величин, каждая из к-рых может принимать лишь два значения 1 или 0 с вероятностями р и 1 - р соответственно. Величины Yi можно трактовать как результаты независимых испытаний, причем Yi = 1 в случае «положительного исхода» и Yi = 0 в случае «отрицательного исхода» испытания с номером i.
М(Х)=np
D(X)=np(1-p)
Распределение Пуассона.
Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0, 1, 2,..., m,... (бесконечное, но счётное множество значений) с вероятностями
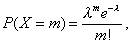 где m=0, 1, 2,...
где m=0, 1, 2,...
Ряд распределения закона Пуассона имеет вид:
xi 0 1 2... m...
pi 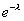
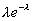
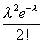 ...
... 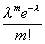 ...
...
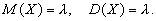
При условии 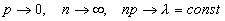 закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Наряду с "предельным" случаем биномиального распределения закон Пуассона может возникнуть и в ряде других случаев. Так для простейшего потока событий число событий, попадающих на произвольный отрезок времени, есть случайная величина, имеющая пуассоновское распределение. Также по закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматической линии, число отказов сложной системы в "нормальном режиме", число "требований на обслуживание", поступивших в единицу времени в системах массового обслуживания, и др.



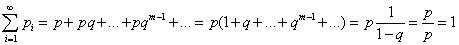
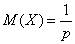
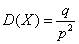 , где q=1-p.
, где q=1-p.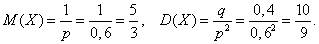
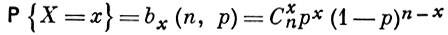
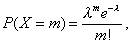 где m=0, 1, 2,...
где m=0, 1, 2,...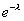
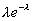
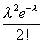 ...
... 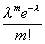 ...
...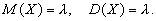
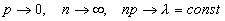 закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.


