А.А.Локшин, Е.А.Иванова
Множества и логика
Аннотация
Локшин А.А., Иванова Е.А. Множества и логика.
В пособии, предназначенном студентам педагогических институтов и колледжей - будущим учителям начальных классов – изложены основы двух важнейших тем, способствующих формированию понятийного мышления.
Рецензенты:
Бахтина О.В.,
канд. пед. наук, доцент кафедры математики и информатики в начальной школе МПГУ;
Сагомонян Е.А.,
Канд. физ.-мат. наук, доцент кафедры волновой и газовой динамики мех-мата МГУ
Предисловие
В этом пособии излагается традиционный материал, акцент сделан на наглядность приводимых доказательств. Первая глава посвящена изложению элементов наивной теории множеств, вторая глава – началам логики. Авторы стремились везде, где это только возможно, использовать диаграммы Эйлера – Венна. Пособие адресовано, в первую очередь, студентам пединститутов и педагогических колледжей - будущим учителям начальных классов.
Москва, 2017
Авторы
Содержание
Глава 1. Элементы наивной теории множеств…….
Глава 2. Элементы математической логики……….
Приложение. Двенадцать иллюстраций………….
Глава 1. Элементы наивной теории множеств
Множество и его элементы
Множеством называют любую неупорядоченную совокупность объектов, каждый из которых называют элементом данного множества.
Объекты, из которых образовано множество, не обязаны обладать каким-либо общим свойством (кроме принадлежности к данному множеству). Обычно обозначать множества мы будем заглавными латинскими буквами (A, B, C, D, …), а элементы множеств, как правило, - строчными латинскими буквами. (Однако для обозначения элементов множеств нам могут понадобиться не только строчные латинские буквы, но и заглавные, а также цифры и другие символы.)
Тот факт, что объект b является элементом множества А, записывается в виде
 А. (1.1)
А. (1.1)
Запись (1.1) читается так:
«b принадлежит множеству А».
Равенство множеств
Два множества А и В равны, если они состоят из одних и тех же элементов. Записывается это так:
А = В. (2.1)
Таким образом, равенство множеств – это их совпадение.
Если множества А и В не равны (не совпадают), это записывается в виде
А  В. (2.2)
В. (2.2)
Пример. Допустим, что у господина Петрова в левой руке зажата копейка и в правой руке зажата копейка. Обозначим через А множество копеек в левой руке Петрова, а через В – множество копеек в правой руке Петрова. Равны ли множества А и В? Очевидно, нет. Эти множества не равны, так как их элементами являются разные объекты.
Подмножества
Если все элементы множества В являются одновременно элементами множества А, то говорят, что В является подмножеством множества А. Обозначается это так:
В  . (3.1)
. (3.1)
Запись (3.1) читается так:
«В включено в А»
или так:
«В содержится в А».
Значок  из формулы (3.1) – это символ нестрогого включения. Запись (3.1) не исключает возможного равенства множеств А и В.
из формулы (3.1) – это символ нестрогого включения. Запись (3.1) не исключает возможного равенства множеств А и В.
Для обозначения того факта, что В является подмножеством множества А и при этом А и В не равны, используется символ строгого включения ⊂. Таким образом, запись
В ⊂ А (3.2)
эквивалентна одновременному выполнению соотношений (3.1) и (2.2).
Замечание. Очевидно, что два множества А и В равны тогда и только тогда, когда каждое из них является подмножеством другого.
Объединение множеств
Пусть А и В – два множества. Их объединением А 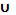 В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А, В.
В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А, В.
Из этого определения, очевидно, следует, что
А 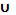 В = В
В = В 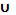 А (8.1)
А (8.1)
(коммутативность операции объединения множеств).
Справедливость соотношения (8.1) часто иллюстрируют на диаграмме Эйлера – Венна (см. рис.8.1).

Делается это следующим образом в два этапа. 1-й этап. Вначале заштриховывают множество А, затем заштриховывают множество В. Все, что заштриховано хотя бы один раз, и есть объединение множеств А 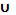 В.
В.
2-й этап. Вначале заштриховывают множество В, затем заштриховывают множество А. Все, что заштриховано хотя бы один раз, и есть объединение множеств В 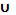 А.
А.
Как видно из рис.8.1, оба раза в результате оказывается заштрихованной (хотя бы один раз) одна и та же область. Тем самым равенство (8.1) считается доказанным.
Аналогично доказывается ассоциативность операции объединения множеств. А именно, для любых трех множеств А, В, С справедливо соотношение:
(А 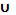 В)
В) 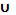 С = А
С = А  В
В 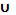 С). (8.2)
С). (8.2)
Справедливы также следующие свойства операции объединения множеств (доказательства не приводим ввиду их очевидности):
А 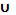 А = А,
А = А,
А 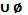 = А,
= А,
А 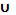 U = U.
U = U.
(Ни в коем случае не следует путать обозначение универсального множества U с обозначением операции объединения множеств 
Замечание. Кроме операции объединения двух множеств, в математике используется операция одновременного объединения нескольких множеств. Пусть, например, имеются множества А i (1 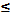 i
i 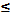 n). Их одновременное объединение
n). Их одновременное объединение 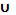 i A i состоит из всех элементов, принадлежащих хотя бы одному из множеств А i . Мы будем считать очевидным, что одновременное объединение трех множеств А, В, С совпадает с (8.2).
i A i состоит из всех элементов, принадлежащих хотя бы одному из множеств А i . Мы будем считать очевидным, что одновременное объединение трех множеств А, В, С совпадает с (8.2).
Пересечение множеств
Пусть снова А и В – два множества. Их пересечением А 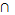 В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В.
В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В.
Из этого определения, очевидно, следует, что
А 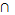 В = В
В = В 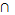 А (9.1)
А (9.1)
(коммутативность операции пересечения множеств).
Справедливость соотношения (9.1) можно проиллюстрировать на диаграмме Эйлера – Венна (см. рис.8.1). Делается это, как и в случае операции объединения множеств, в два этапа.
1-й этап. Вначале заштриховывают множество А, затем заштриховывают множество В. Все, что заштриховано дважды, и есть пересечение множеств А и В.
2-й этап. Вначале заштриховывают множество В, затем заштриховывают множество А. Все, что заштриховано дважды, и есть пересечение множеств В и А.
Как видно из рис.8.1, оба раза в результате оказывается дважды заштрихованной одна и та же область. Тем самым равенство (9.1) считается доказанным.
Аналогично доказывается ассоциативность операции пересечения множеств. А именно, для любых трех множеств А, В, С справедливо соотношение:
(А 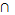 В)
В) 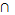 С = А
С = А 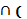 В
В 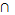 С). (9.2)
С). (9.2)
Справедливы также следующие очевидные свойства операции пересечения множеств (доказательства опускаем ввиду их очевидности):
А 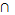 А = А,
А = А,
А 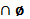 =
= 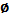 ,
,
А 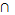 U = А.
U = А.
Законы де Моргана
Справедливы следующие два важных соотношения, называемые законами де Моргана:
(А 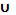 В)’ = А’
В)’ = А’ 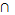 B’ (12.1)
B’ (12.1)
(А 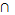 B)’ = А’
B)’ = А’ 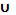 В’ (12.2)
В’ (12.2)
Оба эти соотношения могут быть доказаны при помощи штриховки на диаграмме Эйлера - Венна, а также при помощи логических рассуждений.
Высказывания
Определение 1.1. Высказыванием называется любое повествовательное предложение, о котором можно определенно и однозначно сказать, что оно либо истинно, либо ложно.
Примеры высказываний:
1) «Петя кушает кашу».
2) «Луна – это апельсин».
3) «Дважды два пять».
4) «На каждой елке висят шоколадные конфеты».
5) «В учебнике математики 335 страниц».
Примеры предложений, не являющихся высказываниями:
1) «Мне немного не по себе». (Это повествовательное предложение не является высказыванием, так как неясно, что значит «не по себе» и в каком смысле следует понимать в этом предложении термин «немного».)
2) «Принеси, пожалуйста, кофе». (Это не повествовательное предложение.)
3) «Здравствуйте!» (Это не повествовательное предложение.)
4) «Как пройти на площадь Трех вокзалов?» (Это не повествовательное предложение.)
5) «Я очень рад». (Это повествовательное предложение не является высказыванием, так как невозможно в принципе проверить его истинность. Как отличить «очень рад» от просто «рад»?)
6) «Тише едешь, дальше будешь.» (Это повествовательное предложение представляет собой пословицу, которая не претендует на то, чтобы выражать истину во всех случаях жизни.)
Логические союзы
Важнейшими логическими союзами (без помощи которых мы не могли бы выражать сколько-нибудь сложные мысли) являются следующие:
«и»;
«или» (здесь для определенности имеется в виду неразделительное «или», смысл которого может быть выражен словами «хотя бы одно из двух»);
«не» («неверно, что»);
«если…, то»;
«тогда и только тогда, когда…».
Фактически перечисленные выше союзы представляют собой логические операции, действующие на высказывания. Для этих операций вводятся специальные математические названия и обозначения:
«и» - ⋀ (конъюнкция);
«или» - ⋁ (дизъюнкция);
«не» - ⅂ (отрицание);
«если…, то» - → (импликация);
«тогда, и только тогда, когда…» - ↔ (эквиваленция)
«либо…, либо» - ⩒ (строгая дизъюнкция)
Замечание. В естественном языке один и тот же логический союз может выражаться разными способами. Например, конъюнкция может осуществляться не только при помощи союза «и», но и при помощи союзов «а», «но», при помощи запятой, точки с запятой. При этом появляются (или теряются) какие-то оттенки смысла, не влияющие на истинность/ложность высказывания.
Замечание. Результат перевода предложения с естественного языка на язык логики - это формула, обладающая определенной структурой и принимающая значение истина или ложь. Смысл исходного предложения при этом утрачивается. Однако это не значит, что смысл исходного предложения был несуществен на всех этапах. Для правильного перевода исходного предложения на язык логики необходимо это исходное предложение понимать!
Конъюнкция
| А
| В
| А⋀В
|
| И
| И
| И
|
| И
| Л
| Л
|
| Л
| И
| Л
|
| Л
| Л
| Л
|
Итак, если хотя бы одно из двух высказываний А, В ложно, то их конъюнкция ложна. Если же оба высказывания А, В истинны, то истинна и их конъюнкция. Такое определение вполне соответствует употреблению союза «и» в естественном языке.
Дизъюнкция
| А
| В
| А⋁В
|
| И
| И
| И
|
| И
| Л
| И
|
| Л
| И
| И
|
| Л
| Л
| Л
|
Представленная таблица истинности для дизъюнкции также превосходно согласуется с употреблением в естественном языке неразделительного союза «или».
:
Отрицание
Итак, при любых обстоятельствах исходное высказывание А и его отрицание ⅂А должны иметь противоположные значения истинности. Приведем пример, поясняющий сказанное.
Пример.
А: «Петя кушает кашу».
Возможные способы отрицания:
а) Универсальный способ, всегда приводящий к правильному результату:
⅂А: «Неверно, что Петя кушает кашу»
б) Постановка частицы «не» перед сказуемым (этот способ не всегда приводит к правильному результату):
⅂А: «Петя не кушает кашу»
Замечание. Попробуем в предыдущем примере поставить частицу «не» иначе, чем это сделано в пункте б) (т.е. не перед сказуемым). Например,
В: «Петя кушает не кашу»
Высказывание В не является отрицанием для А, так как в принципе возможна ситуация, когда “ Петя ничего не кушает ”; в этом случае, очевидно
А = В = Л,
тем самым В  ⅂А.
⅂А.
Замечание. Покажем, что постановка частицы «не» перед сказуемым не всегда приводит к правильной формулировке отрицания.
Рассмотрим высказывание:
С: «Некоторые люди боятся мышей»
С’: «Некоторые люди не боятся мышей»
Итак, мы поставили частицу «не» перед сказуемым, но очевидно, что
C’  ⅂C.
⅂C.
В дальнейшем мы более подробно обсудим возникшую здесь ситуацию.
Импликация
| А
| В
| А → В
|
| И
| И
| И
|
| И
| Л
| Л
|
| Л
| И
| И
|
| Л
| Л
| И
|
Импликация – наиболее трудная для усвоения и восприятия логическая операция (и при этом, возможно, наиболее важная). Обсудим возникающие здесь проблемы.
Замечание 1.
Рассмотрим вначале первую строчку таблицы. Пусть
А: «Париж – столица Франции»
В: «В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы»
Очевидно, что А = В = И, поэтому истинно также высказывание А→В:
А→В = И
Прочтем теперь высказывание А→В на естественном языке:
«Если Париж – столица Франции, то в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы» (5.1)
Высказывание (5.1) истинно, но оно ни в коем случае не является доказательством теоремы Пифагора. Дело обстоит как раз наоборот: так как мы знаем, что теорема Пифагора верна, то мы можем (в соответствии с таблицей истинности для импликации) заключить, что высказывание (5.1) истинно.
Замечание 2.
Вторая строчка таблицы не вызывает сомнений. Поэтому перейдем к объяснению третьей и четвертой строчек нашей таблицы.
Рассмотрим высказывание:
C: «Если число страниц в моей книге больше пятисот, то оно больше трехсот.»
Мы воспринимаем это утверждение как истинное вообще, независимо от того, сколько страниц в моей книге. Очевидно, что логическая структура высказывания С имеет вид:
С = А→В, (5.2)
где
А: «Число страниц в моей книге больше пятисот»,
В: «Число страниц в моей книге больше трехсот».
Обозначим реальное число страниц в моей книге через w.
Если w > 500, то (5.2) имеет вид
С = И→И,
т.е. мы попадаем в первую строчку нашей таблицы, и истинность высказывания С (которая нам казалась естественной с самого начала) согласуется со значением И, стоящим в третьем столбце.
Пусть теперь 300 <w 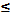 500. В этом случае (5.2) приобретает вид
500. В этом случае (5.2) приобретает вид
С = Л→И,
т.е. мы попадаем в третью строчку таблицы, и снова истинность С согласуется со значением И, стоящим в третьем столбце.
Аналогично, рассматривается случай w 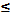 300. В этом случае (5.2) имеет вид
300. В этом случае (5.2) имеет вид
С = Л→Л,
т.е. мы попадаем в четвертую строчку таблицы, и снова истинность С согласуется со значением И, стоящим в третьем столбце.
Эквиваленция
| А
| В
| А↔В
|
| И
| И
| И
|
| И
| Л
| Л
|
| Л
| И
| Л
|
| Л
| Л
| И
|
Представленная таблица истинности для эквиваленции вполне согласуется с употреблением в естественном языке союза «тогда и только тогда, когда…».
Замечание. Определяя действие логических союзов, мы воспользовались таблицами, которые, в сущности, представляют собой краткую запись словесного описания. Если мы захотим прочесть вслух любую из этих таблиц, то неизбежно воспользуемся в нашей речи теми логическими союзами, которым даем определение. Вернемся, например, к таблице, определяющей импликацию, и попробуем прочесть ее первую строчку. Вот, что у нас получится:
Если А = И и В = И, то А⋀В = И.
Здесь подчеркнуты и выделены жирным шрифтом логические союзы естественного языка («если…, то», «и»»), которые мы фактически использовали, чтобы определить логический союз «и» языка логики. Для того, чтобы избавиться от неизбежно возникающего здесь порочного круга, в математике принято различать язык логики и метаязык, т.е. естественный язык, на котором комментируются высказывания, сделанные на языке логики.
Закон силлогизма
А→В
В→С
А→С (8.4)
Проверяется по таблицам истинности. См. также рис. 8.1, где Си - круг, внутри которого С = И, а вне которого С = Л.

9. Предикаты: определение, примеры
Определение 9.1. Одноместнымпредикатом А(х)называется повествовательное предложение, содержащее одну переменную х и превращающееся в высказывание при подстановке вместо этой переменной ее конкретных значений. (Для обозначения переменной, входящей в предикат, может использоваться любая буква латинского или русского алфавита.)
Определение 9.2. Множество всех тех значений переменной х, при подстановке которых в предикат А(х) получается (осмысленное) высказывание, называется областью определения данного предиката.
Определение 9.3. Множество всех тех значений переменной х, при подстановке которых в предикат А(х) получается истинное высказывание, называется множеством истинности данного предиката и обозначается Аи .
Определение 9.4. Если множество истинности предиката А(х) совпадает с областью его определения, то такой предикат называют тождественно истинным и пишут А(х) = И.
Если множество истинности предиката А(х) пусто, то такой предикат называют тождественно ложным и пишут А(х) = Л.
Определение 9.5. Два предиката А(х) и В(х), у которых множества истинности совпадают, мы будем называть эквивалентными и писать
А(х) = В(х).
Пример. «Писатель х написал роман ”Война и мир”». Область определения этого предиката – множество всех писателей. Множество истинности этого предиката состоит из Л.Н.Толстого.
Пример.
А(х): «х + х = 3 – х».
Это уравнение – одноместный (а не трехместный!) предикат. Его область определения – множество всех действительных чисел, а его множество истинности есть {1}.
Пример.
В(y): «(y – 1)(y –2) = 0».
Это уравнение – также одноместный предикат, его область определения – множество всех действительных чисел, а его множество истинности есть {1; 2}.
Пример.
С(z): «1 + z = z + 1».
C(z) – тождественно истинный предикат.
Операции над предикатами
Пусть
А(х), В(х), С(х), … (10.1)
- одноместные предикаты. Логические операции над ними определяются при каждом фиксированном х как над высказываниями. Поэтому все законы (6.1) – (6.23) сохраняют свою силу и для предикатов.
Квантор общности
Для определенности, будем в этом разделе говорить об одноместных предикатах, зависящих от переменной х; областью определения рассматриваемых предикатов считаем множество Х.
Определение 13.1. Квантором общности называют выражение
«для каждого х» (13.1)
- это краткая форма записи; либо выражение
«для каждого х  Х» (13.1’)
Х» (13.1’)
- это подробная форма записи.
Для обозначения квантора общности используют специальный значок - перевернутую букву А (от английского слова all). В результате краткая запись приобретает вид: ( х), а подробная запись – вид: (
х), а подробная запись – вид: ( х
х  Х).
Х).
Замечание. Синонимами выражения (13.1) являются следующие словосочетания: «для всех х», «для любого х», «для всякого х». Аналогичное замечание справедливо и для выражения (13.1’).
Пусть теперь P(x) – некоторый предикат; постановка квантора общности перед ним превращает его в высказывание
( х)P(x) (13.2)
х)P(x) (13.2)
или, в подробной записи,
( х
х  Х)P(x). (13.2’)
Х)P(x). (13.2’)
Замечание. Говорят, что квантор ( х) связывает переменную х; в выражениях (13.2) и (13.2’) переменная х считается связанной (до постановки квантора (
х) связывает переменную х; в выражениях (13.2) и (13.2’) переменная х считается связанной (до постановки квантора ( х) эта же переменная была свободной).
х) эта же переменная была свободной).
Пример. Рассмотрим высказывание на естественном языке:
С: «Каждый человек носит шляпу».
Логическая структура этого предложения такова:
( х
х  Х)P(x);
Х)P(x);
здесь Х – множество всех людей, P(x) – предикат «х носит шляпу».
Нетрудно понять, что высказывание С ложно (т.к. существуют люди, которые не носят шляпу).
Квантор существования
Определение 14.1. Квантором существования называют выражение
«существует х такой, что» (14.1)
- это краткая форма записи; либо выражение
«существует х  Х такой, что» (14.1’)
Х такой, что» (14.1’)
- это подробная форма записи.
Замечание. В естественном языке роль квантора существования выполняют также словосочетания: «найдется х такой, что», «для некоторых х».
Для обозначения квантора существования используют специальный значок - отраженную по горизонтали букву Е (от английского слова exist). В результате краткая запись приобретает вид: ( х), а подробная запись – вид: (
х), а подробная запись – вид: ( х
х  Х).
Х).
Квантор существования (как и квантор общности) связывает соответствующую переменную и превращает предикат в высказывание.
Пример. Рассмотрим высказывание:
D: «У некоторых людей четырнадцать ног».
Логическая структура этого предложения такова:
( х
х  Х)Q(x);
Х)Q(x);
здесь Х – множество всех людей, Q(x) – предикат «х имеет четырнадцать ног».
Высказывание D, очевидно, ложно, так как не существует ни одного человека с 14-ю ногами.
Пример 2.
Некоторые розы – красные
Ни одна собака не красная
Ни один фокстерьер не красный (17.3)
Фокстерьеры – это собаки
Мы предоставляем читателю возможность переписать (17.3) «на языке предикатов и кванторов», а вместо этого запишем это умозаключение сразу в менее громоздком виде «на языке множеств»:
Pи 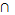 Ки
Ки 
Си  (Kи)’
(Kи)’
Фи  (Kи)’
(Kи)’
Фи  Cи (17.3’)
Cи (17.3’)
Здесь Ри - множество роз (т.е. множество истинности предиката «х – роза»);
Ки - множество красных объектов (т.е. множество истинности предиката «х – красный»);
Си - множество собак (т.е. множество истинности предиката «х – собака»);
Фи - множество фокстерьеров (т.е множество истинности предиката «х – фокстерьер»).
Все посылки нашего умозаключения (17.3), а также его вывод – истинны. Но правильна ли форма этого умозаключения? Для того чтобы получить ответ на этот вопрос, посмотрим на рис. 17.2.

Мы видим, что все требования, которые обеспечивают истинность посылок в (17.3’), соблюдены на рис. 17.2, но ожидаемого вывода мы не получили. Это как раз и означает, что форма нашего умозаключения – неправильная.
Пример 3.
Ни одна кукушка не умеет читать
Некоторые утки умеют плавать
Некоторые утки – не кукушки (17.4)
Сразу же перепишем умозаключение (17.4) «на языке множеств»:
Ки  (Чи)’
(Чи)’
Уи 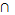 Пи
Пи 
Уи 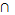 (Ки)’
(Ки)’  (17.4’)
(17.4’)
Здесь Ки – множество кукушек; Чи – множество существ, умеющих читать;
Уи – множество уток; Пи – множество существ, умеющих плавать.
Снова посылки и вывод – истинные высказывания, но, как видно из рис. 17.3, истинность посылок не обеспечивает истинность вывода. Поэтому форма умозаключения (17.4) – неправильная.

Приложение. Двенадцать иллюстраций











А.А.Локшин, Е.А.Иванова
Множества и логика
Аннотация
Локшин А.А., Иванова Е.А. Множества и логика.
В пособии, предназначенном студентам педагогических институтов и колледжей - будущим учителям начальных классов – изложены основы двух важнейших тем, способствующих формированию понятийного мышления.
Рецензенты:
Бахтина О.В.,
канд. пед. наук, доцент кафедры математики и информатики в начальной школе МПГУ;
Сагомонян Е.А.,
Канд. физ.-мат. наук, доцент кафедры волновой и газовой динамики мех-мата МГУ
Предисловие
В этом пособии излагается традиционный материал, акцент сделан на наглядность приводимых доказательств. Первая глава посвящена изложению элементов наивной теории множеств, вторая глава – началам логики. Авторы стремились везде, где это только возможно, использовать диаграммы Эйлера – Венна. Пособие адресовано, в первую очередь, студентам пединститутов и педагогических колледжей - будущим учителям начальных классов.
Москва, 2017
Авторы
Содержание
Глава 1. Элементы наивной теории множеств…….
Глава 2. Элементы математической логики……….
Приложение. Двенадцать иллюстраций………….
Глава 1. Элементы наивной теории множеств
Множество и его элементы
Множеством называют любую неупорядоченную совокупность объектов, каждый из которых называют элементом данного множества.
Объекты, из которых образовано множество, не обязаны обладать каким-либо общим свойством (кроме принадлежности к данному множеству). Обычно обозначать множества мы будем заглавными латинскими буквами (A, B, C, D, …), а элементы множеств, как правило, - строчными латинскими буквами. (Однако для обозначения элементов множеств нам могут понадобиться не только строчные латинские буквы, но и заглавные, а также цифры и другие символы.)
Тот факт, что объект b является элементом множества А, записывается в виде
 А. (1.1)
А. (1.1)
Запись (1.1) читается так:
«b принадлежит множеству А».
Равенство множеств
Два множества А и В равны, если они состоят из одних и тех же элементов. Записывается это так:
А = В. (2.1)
Таким образом, равенство множеств – это их совпадение.
Если множества А и В не равны (не совпадают), это записывается в виде
А  В. (2.2)
В. (2.2)
Пример. Допустим, что у господина Петрова в левой руке зажата копейка и в правой руке зажата копейка. Обозначим через А множество копеек в левой руке Петрова, а через В – множество копеек в правой руке Петрова. Равны ли множества А и В? Очевидно, нет. Эти множества не равны, так как их элементами являются разные объекты.
Подмножества
Если все элементы множества В являются одновременно элементами множества А, то говорят, что В является подмножеством множества А. Обозначается это так:
В  . (3.1)
. (3.1)
Запись (3.1) читается так:
«В включено в А»
или так:
«В содержится в А».
Значок  из формулы (3.1) – это символ нестрогого включения. Запись (3.1) не исключает возможного равенства множеств А и В.
из формулы (3.1) – это символ нестрогого включения. Запись (3.1) не исключает возможного равенства множеств А и В.
Для обозначения того факта, что В является подмножеством множества А и при этом А и В не равны, используется символ строгого включения ⊂. Таким образом, запись
В ⊂ А (3.2)
эквивалентна одновременному выполнению соотношений (3.1) и (2.2).
Замечание. Очевидно, что два множества А и В равны тогда и только тогда, когда каждое из них является подмножеством другого.





 А. (1.1)
А. (1.1) В. (2.2)
В. (2.2) . (3.1)
. (3.1) из формулы (3.1) – это символ нестрогого включения. Запись (3.1) не исключает возможного равенства множеств А и В.
из формулы (3.1) – это символ нестрогого включения. Запись (3.1) не исключает возможного равенства множеств А и В. В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А, В.
В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А, В.
 В
В 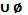 = А,
= А,
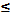 i
i 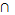 В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В.
В называется множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В.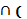 В
В 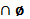 =
= 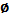 ,
,
 Х» (13.1’)
Х» (13.1’) х), а подробная запись – вид: (
х), а подробная запись – вид: ( Х).
Х). х), а подробная запись – вид: (
х), а подробная запись – вид: (


















