Вопросы к теме
1. Основы теории множеств.
2. Элементы математической логики.
Краткие теоретические сведения
Основы теории множеств
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга.
Пример: Множество S страниц в данной методичке. Множество 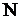 натуральных чисел
натуральных чисел 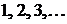 Множество
Множество 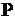 простых чисел
простых чисел 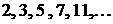 Множество
Множество 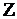 целых чисел:
целых чисел: 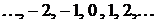 Множество R вещественных чисел. Множество A различных символов на этой странице.
Множество R вещественных чисел. Множество A различных символов на этой странице.
Если объект 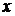 является элементом множества
является элементом множества 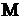 , то говорят, что
, то говорят, что 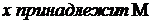 (Обозначение:
(Обозначение: 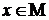 ). В противном случае говорят, что
). В противном случае говорят, что 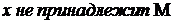 (Обозначение:
(Обозначение: 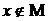 ).
).
Множества, как объекты, могут быть элементами других множеств. Множество, элементами которого являются множества, обычно называется классом или семейством.
Множество, не содержащее элементов, называется пустым.
Обозначение: 
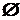
Чтобы задать множество, нужно указать, какие элементы ему принадлежат.
Это можно сделать различными способами:
перечисление элементов: 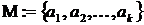 (обозначения элементов обычно заключают в фигурные скобки и разделяются запятыми);
(обозначения элементов обычно заключают в фигурные скобки и разделяются запятыми);
характеристическим предикатом: 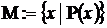 (это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение: если для данного элемента условие выполнено, то он принадлежит определенному множеству, в противном случае – не принадлежит);
(это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение: если для данного элемента условие выполнено, то он принадлежит определенному множеству, в противном случае – не принадлежит);
порождающей процедурой: 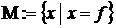 (процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества).
(процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества).
Примеры: 1. 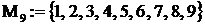 ;
;
2. 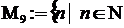 &
& 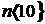
Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.
Множество целых чисел в диапазоне от m до n обозначается так: m…n. То есть 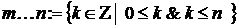 ;
;
Множество A содержится в множестве B (множество B включает множество A), если каждый элемент A есть элемент B: 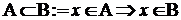 .
.
В этом случае 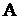 называется подмножеством
называется подмножеством 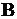 ,
, 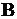 - надмножеством
- надмножеством 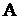 . Если
. Если 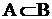 и
и 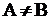 , то
, то 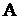 называется собственным подмножеством
называется собственным подмножеством 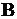 .
.
Два множества равны, если они являются подмножествами друг друга: 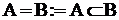 &
& 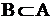 .
.
Мощностью множества 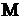 обозначатся
обозначатся 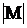 . Для конечных множеств мощность – это число элементов. Если
. Для конечных множеств мощность – это число элементов. Если 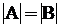 , то множества
, то множества 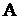 и
и 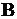 называются равномощными.
называются равномощными.
Операции над множествами:
- объединение : 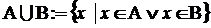 ;
;
- персечение : 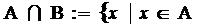 &
& 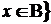 ;
;
- разность : 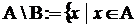 &
& 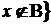 ;
;
- симметрическаяразность : 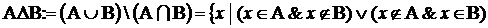
- дополнение : 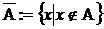 .
.
Операция дополнения подразумевает универсум 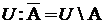 .
.
Пример: Пусть 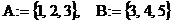 .
.
Тогда 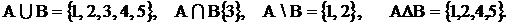
Диаграммы Эйлера, иллюстрируют операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).

Свойства операций над множествами :
Пусть задан универсум 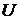 . Тогда
. Тогда 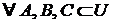 выполняются следующие свойства.
выполняются следующие свойства.
1. идемпотентность: 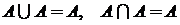 ;
;
2. коммутативность: 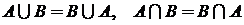 ;
;
3. ассоциативность: 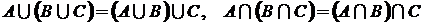 ;
;
4. дистрибутивность:
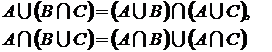
5. поглощение: 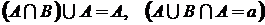 ;
;
6. свойство нуля: 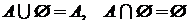 ;
;
7. свойство единицы: 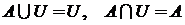 ;
;
8. инволютивность: 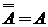 ;
;
9. законы Моргана: 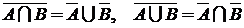 ;
;
10. свойства дополнения: 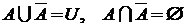 ;
;
11. выражение для разности: 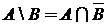 .
.
В справедливости перечисленных свойств можно убедиться различными способами. Например, нарисовать диаграммы Эйлера для левой и правой частей равенства, и убедится, что они совпадают.
Элементы математической логики (алгебры логики)
Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра функций, алгебра векторов и так далее). Объектами алгебры логики являются высказывания.
Высказывание – это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.
О предметах можно судить верно или неверно, то есть высказывание может быть истинным ( обозначается 1 ) или ложным ( обозначается 0).
Высказывание называется простым, если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называется составным (сложным).
Например, А = {Аристотель – основоположник логики}
В = {Лондон – столица Парижа}
Таким образом, А = 1, В = 0.
Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре логики заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.
Логические операции
1. Конъюнкция (логическое умножение)
· в естественном языке соответствует союзу И;
· обозначается & или 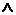
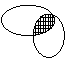 Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Диаграмма Эйлера-Венна соответствует пересечению множеств.
Таблица истинности
2. Дизъюнкция (логическое сложение)
· в естественном языке соответствует союзу ИЛИ;
· обозначается 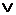
Дизъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
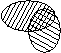 Диаграмма Эйлера-Венна соответствует объединению множеств.
Диаграмма Эйлера-Венна соответствует объединению множеств.
Таблица истинности
| А
| В
| А 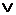 В В
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Инверсия (отрицание)
· в естественном языке соответствует словам НЕВЕРНО, ЧТО… и частице НЕ;
· обозначается 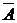
Инверсия – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Таблица истинности
| А
| 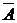
|
|
|
|
|
|
|
Диаграмма Эйлера-Венна
4. Импликация (логическое следование)
· в естественном языке соответствует обороту ЕСЛИ …, ТО…
· обозначение 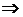
Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Таблица истинности
| А
| В
| А 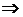 В В
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Эквиваленция (равнозначность)
· в естественном языке соответствует обороту ТОГДА И ТОЛЬКО ТОГДА, КОГДА…
· обозначение 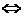
Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Таблица истинности
| А
| В
| А 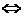 В В
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последовательности и ряды
Вопросы к теме
1. Числовые ряды Знакопеременные ряды.
2. Степенные ряды.
3. Признаки сходимости ряда
Краткие теоретические сведения
Числовым рядом называется сумма вида 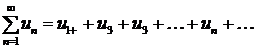 , где числа
, где числа 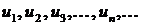 , называемые членами ряда, образуют бесконечную последовательность; член
, называемые членами ряда, образуют бесконечную последовательность; член 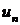 называется общим членом ряда.
называется общим членом ряда.
Суммы 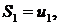

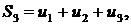
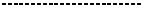
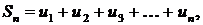
Составленные из первых членов ряда, называются частными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм 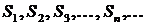 . Если при бесконечном возрастании номера
. Если при бесконечном возрастании номера 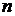 частичная сумма ряда
частичная сумма ряда 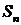 стремится к пределу
стремится к пределу 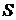 , то ряд называется сходящимся, а число
, то ряд называется сходящимся, а число 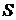 - суммой сходящегося ряда, т.е.
- суммой сходящегося ряда, т.е. 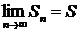 или
или 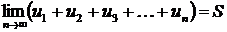 . Эта запись равносильна записи
. Эта запись равносильна записи 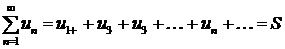 .
.
Если частичная сумма 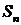 ряда при неограниченном возрастании
ряда при неограниченном возрастании 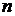 не имеет конечного предела (в частности, стремится к
не имеет конечного предела (в частности, стремится к 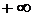 или
или 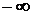 ), то такой ряд называется расходящимся.
), то такой ряд называется расходящимся.
Если ряд сходится, то значение 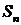 при достаточно большом
при достаточно большом 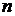 является приближенным выражением суммы ряда
является приближенным выражением суммы ряда 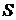 .
.
Разность 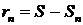 называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е.
называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 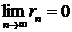 , и наоборот, если остаток стремится к нулю, то ряд сходится.
, и наоборот, если остаток стремится к нулю, то ряд сходится.
Пример: записать ряд по его заданному общему члену 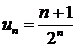 .
.
Полагая 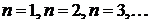 , имеет бесконечную последовательность чисел:
, имеет бесконечную последовательность чисел: 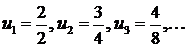 . Сложив ее члены, получим ряд
. Сложив ее члены, получим ряд 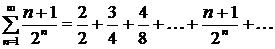 .
.
Пример: записать ряд по его заданному общему члену 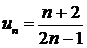 .
.
Полагая 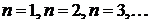 , имеет бесконечную последовательность чисел:
, имеет бесконечную последовательность чисел: 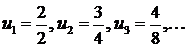 . Сложив ее члены, получим ряд
. Сложив ее члены, получим ряд 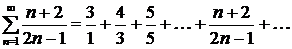 .
.
Пример: записать ряд по его заданному общему члену 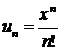 .
.
Полагая 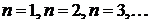 и учитывая, что
и учитывая, что 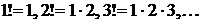 , получим ряд
, получим ряд 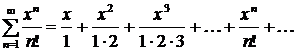 .
.
Пример: найти 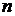 - й член ряда по его данным первым членам
- й член ряда по его данным первым членам 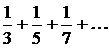 .
.
Знаменатели членов ряда, начиная с третьего, являются нечетными числами; следовательно, 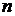 - й член ряда имеет вид
- й член ряда имеет вид 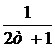 .
.
Пример: найти 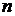 - й член ряда по его данным первым членам
- й член ряда по его данным первым членам 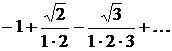 .
.
Числители членов ряда представляют собой квадратные корни из натуральных чисел, а их соответствующие знаменатели равны 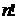 . Знаки чередуются по закону
. Знаки чередуются по закону 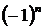 . Общий член ряда имеет вид
. Общий член ряда имеет вид 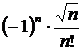 .
.
Пример: найти 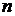 - й член ряда по его данным первым членам
- й член ряда по его данным первым членам 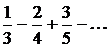 .
.
Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с 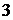 . Знаки чередуются по закону
. Знаки чередуются по закону 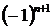 или по закону
или по закону 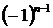 . Значит
. Значит 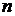 - й член ряда имеет вид или
- й член ряда имеет вид или 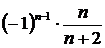 .
.
Пример: найти сумму членов ряда 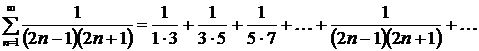 .
.
Находим частичные суммы членов ряда:
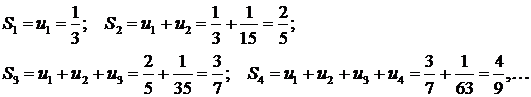
Запишем последовательность частичных сумм: 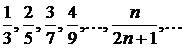 . Общий член этой последовательности есть
. Общий член этой последовательности есть 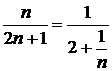 . Следовательно,
. Следовательно, 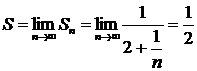 . Последовательность частичных сумм имеет предел, равный
. Последовательность частичных сумм имеет предел, равный 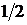 . Итак, ряд сходится и его сумма равна
. Итак, ряд сходится и его сумма равна 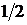 .
.
Необходимый признак сходимости ряда
Ряд 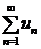 может сходится только при условии, что его общий член
может сходится только при условии, что его общий член 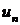 при неограниченном увеличении номера
при неограниченном увеличении номера 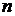 стремится к нулю:
стремится к нулю: 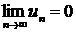 .
.
Если 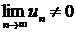 , то ряд
, то ряд 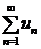 расходится – это достаточный признак расходимости ряда.
расходится – это достаточный признак расходимости ряда.
Пример: Исследовать сходимость ряда, применяя необходимый признак сходимости 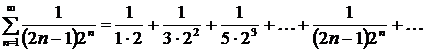 .
.
Находим 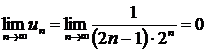 . Необходимый признак сходимости ряда выполняется.
. Необходимый признак сходимости ряда выполняется.
Пример: Исследовать сходимость ряда, применяя необходимый признак сходимости 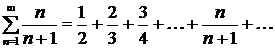 .
.
Имеем 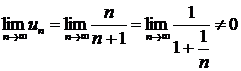 . Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.
. Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.
Пример: Исследовать сходимость ряда, применяя необходимый признак сходимости 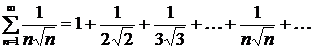 .
.
Находим 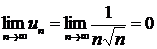 . Необходимый признак сходимости ряда выполняется.
. Необходимый признак сходимости ряда выполняется.
Достаточный признак сходимости ряда с положительными членами
Признак Даламбера: Если для ряда с положительными членами 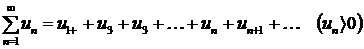 выполняется условие
выполняется условие 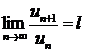 , то ряд сходится при
, то ряд сходится при 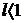 и расходится при
и расходится при 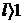 .
.
Признак Даламбера не дает ответа, если 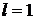 . В этом случае для исследования применяются другие приемы.
. В этом случае для исследования применяются другие приемы.
Пример: Исследовать сходимость ряда, используя признак Даламбера 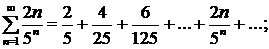
Подставив в общий член ряда 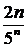 вместо n число n+1, получим
вместо n число n+1, получим 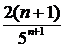 . Найдем предел отношения (n+1) –го члена к n –му члену при n
. Найдем предел отношения (n+1) –го члена к n –му члену при n 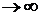 :
:
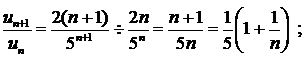
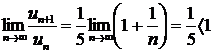 . Следовательно, данный ряд сходится.
. Следовательно, данный ряд сходится.
Числовые последовательности
Под числовой последовательностью 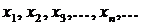 понимается функция
понимается функция 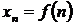 заданная на множестве
заданная на множестве 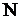 натуральных чисел. Кратко последовательность обозначается в виде
натуральных чисел. Кратко последовательность обозначается в виде 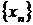 или
или 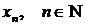 . Число
. Число 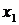 называется первым членом (элементом) последовательности,
называется первым членом (элементом) последовательности, 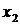 - вторым, …,
- вторым, …, 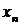 - общим или
- общим или 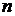 -м членом последовательности.
-м членом последовательности.
Чаще всего последовательность задается формулой его общего члена. Формула 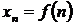 позволяет вычислить любой член последовательности по номеру
позволяет вычислить любой член последовательности по номеру 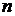 .
.
Так, равенства 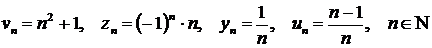
Задают соответственно последовательности
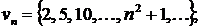
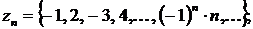
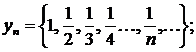
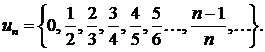
Последовательность 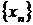 называется ограниченной, если существует такое число
называется ограниченной, если существует такое число 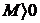 , что для любого
, что для любого 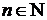 выполняется неравенство
выполняется неравенство 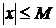 . В противном случае последовательность называется неограниченной. Легко видеть, что последовательности
. В противном случае последовательность называется неограниченной. Легко видеть, что последовательности 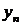 и
и 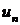 ограничены, а
ограничены, а 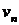 и
и 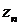 - неограниченны.
- неограниченны.
Последовательность 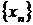 называется возрастающей (неубывающей), если для любого
называется возрастающей (неубывающей), если для любого 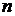 выполняется неравенство
выполняется неравенство 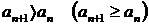 . Аналогично определяется убывающая (невозрастающая) последовательность.
. Аналогично определяется убывающая (невозрастающая) последовательность.
Все эти последовательности называются монотонными последовательностями. Последовательности 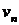 ,
, 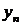 и
и 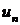 монотонные, а
монотонные, а 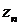 - не монотонная.
- не монотонная.
Если все элементы последовательности 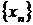 равны одному и тому же числу
равны одному и тому же числу 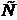 , то ее называют постоянной.
, то ее называют постоянной.
Другой способ задания числовых последовательностей – рекуррентный способ. В нем задается начальный элемент 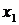 (первый член последовательности) и правило определения
(первый член последовательности) и правило определения 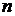 -го элемента по
-го элемента по 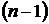 -му:
-му: 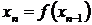 . Таким образом,
. Таким образом, 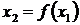 ,
, 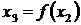 и т.д. При таком способе задания последовательности для определения
и т.д. При таком способе задания последовательности для определения 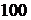 -го члена надо сначала посчитать все
-го члена надо сначала посчитать все  предыдущих.
предыдущих.
Степенные ряды
Степенным рядом называется ряд вида 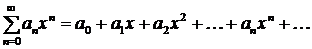 , где числа
, где числа 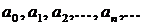 называются коэффициентами ряда, а член
называются коэффициентами ряда, а член 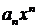 - общим членом ряда.
- общим членом ряда.
Областью сходимости степенного ряда называется множество всех значений 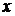 , при которых данный ряд сходится.
, при которых данный ряд сходится.
Число 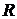 называется радиусом сходимости степенного ряда, если при
называется радиусом сходимости степенного ряда, если при 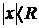 ряд сходится и при том абсолютно, а при
ряд сходится и при том абсолютно, а при 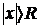 ряд расходится.
ряд расходится.
Если существует предел 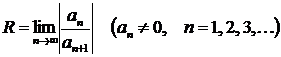 , то радиус сходимости ряда
, то радиус сходимости ряда 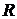 равен этому пределу и степенной ряд сходится при
равен этому пределу и степенной ряд сходится при 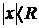 , т.е. в промежутке
, т.е. в промежутке 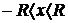 , который называется промежутком (интервалом) сходимости.
, который называется промежутком (интервалом) сходимости.
Если предел равен нулю 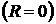 , то степенной ряд сходится в единственной точке
, то степенной ряд сходится в единственной точке 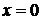 .
.
На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходится. Сходимость степенного ряда при 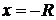 и
и 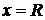 исследуется с помощью какого-либо из признаков сходимости.
исследуется с помощью какого-либо из признаков сходимости.
Пример: дан ряд 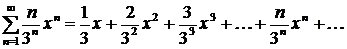 . Исследовать его сходимость в точках
. Исследовать его сходимость в точках 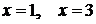 .
.
При 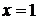 данный ряд превращается в числовой ряд
данный ряд превращается в числовой ряд 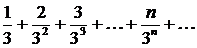 . Исследуем сходимость этого ряда по признаку Даламбера. Имеем
. Исследуем сходимость этого ряда по признаку Даламбера. Имеем 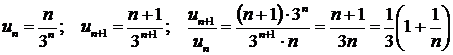 ;
;
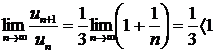 , т.е. ряд сходится.
, т.е. ряд сходится.
При  получим ряд
получим ряд 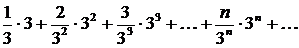 или
или 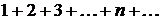 , который расходится, так как не выполняется необходимый признак сходимости ряда
, который расходится, так как не выполняется необходимый признак сходимости ряда 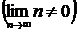 .
.



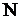 натуральных чисел
натуральных чисел 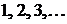 Множество
Множество 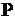 простых чисел
простых чисел 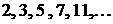 Множество
Множество 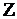 целых чисел:
целых чисел: 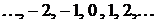 Множество R вещественных чисел. Множество A различных символов на этой странице.
Множество R вещественных чисел. Множество A различных символов на этой странице.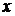 является элементом множества
является элементом множества 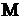 , то говорят, что
, то говорят, что 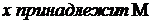 (Обозначение:
(Обозначение: 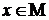 ). В противном случае говорят, что
). В противном случае говорят, что 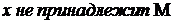 (Обозначение:
(Обозначение: 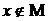 ).
).
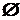
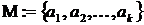 (обозначения элементов обычно заключают в фигурные скобки и разделяются запятыми);
(обозначения элементов обычно заключают в фигурные скобки и разделяются запятыми);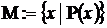 (это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение: если для данного элемента условие выполнено, то он принадлежит определенному множеству, в противном случае – не принадлежит);
(это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение: если для данного элемента условие выполнено, то он принадлежит определенному множеству, в противном случае – не принадлежит);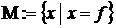 (процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества).
(процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества).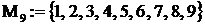 ;
;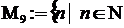 &
& 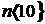
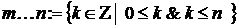 ;
;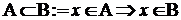 .
.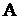 называется подмножеством
называется подмножеством 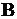 ,
, 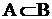 и
и 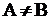 , то
, то 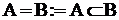 &
& 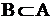 .
.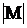 . Для конечных множеств мощность – это число элементов. Если
. Для конечных множеств мощность – это число элементов. Если 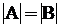 , то множества
, то множества 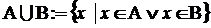 ;
;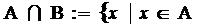 &
& 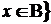 ;
;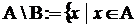 &
& 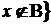 ;
;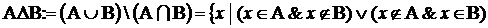
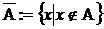 .
.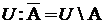 .
.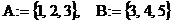 .
.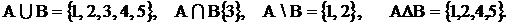

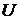 . Тогда
. Тогда 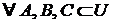 выполняются следующие свойства.
выполняются следующие свойства.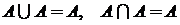 ;
;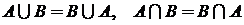 ;
;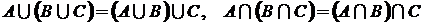 ;
;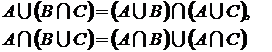
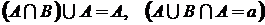 ;
;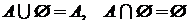 ;
;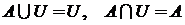 ;
;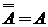 ;
;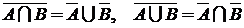 ;
;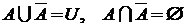 ;
;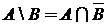 .
.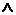
 Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.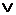
 Диаграмма Эйлера-Венна соответствует объединению множеств.
Диаграмма Эйлера-Венна соответствует объединению множеств.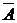

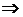
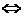
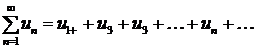 , где числа
, где числа 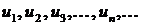 , называемые членами ряда, образуют бесконечную последовательность; член
, называемые членами ряда, образуют бесконечную последовательность; член 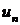 называется общим членом ряда.
называется общим членом ряда.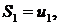

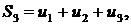
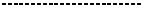
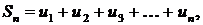
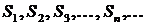 . Если при бесконечном возрастании номера
. Если при бесконечном возрастании номера 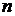 частичная сумма ряда
частичная сумма ряда 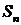 стремится к пределу
стремится к пределу 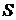 , то ряд называется сходящимся, а число
, то ряд называется сходящимся, а число 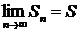 или
или 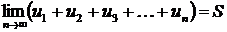 . Эта запись равносильна записи
. Эта запись равносильна записи 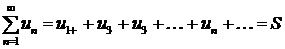 .
.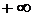 или
или 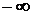 ), то такой ряд называется расходящимся.
), то такой ряд называется расходящимся.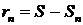 называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е.
называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 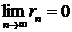 , и наоборот, если остаток стремится к нулю, то ряд сходится.
, и наоборот, если остаток стремится к нулю, то ряд сходится.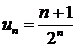 .
.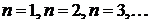 , имеет бесконечную последовательность чисел:
, имеет бесконечную последовательность чисел: 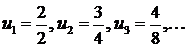 . Сложив ее члены, получим ряд
. Сложив ее члены, получим ряд 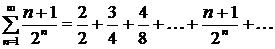 .
.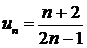 .
.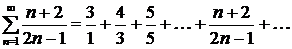 .
.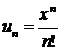 .
.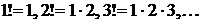 , получим ряд
, получим ряд 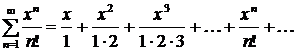 .
.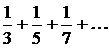 .
.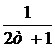 .
.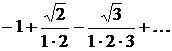 .
.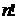 . Знаки чередуются по закону
. Знаки чередуются по закону 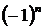 . Общий член ряда имеет вид
. Общий член ряда имеет вид 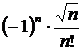 .
.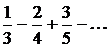 .
.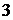 . Знаки чередуются по закону
. Знаки чередуются по закону 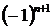 или по закону
или по закону 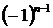 . Значит
. Значит 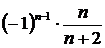 .
.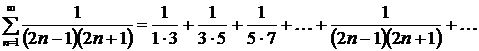 .
.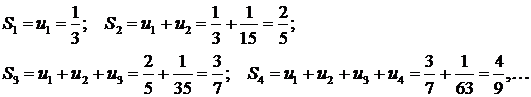
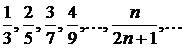 . Общий член этой последовательности есть
. Общий член этой последовательности есть 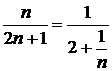 . Следовательно,
. Следовательно, 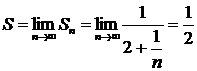 . Последовательность частичных сумм имеет предел, равный
. Последовательность частичных сумм имеет предел, равный 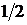 . Итак, ряд сходится и его сумма равна
. Итак, ряд сходится и его сумма равна 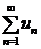 может сходится только при условии, что его общий член
может сходится только при условии, что его общий член 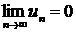 .
.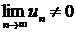 , то ряд
, то ряд 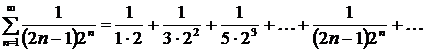 .
.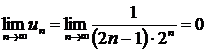 . Необходимый признак сходимости ряда выполняется.
. Необходимый признак сходимости ряда выполняется.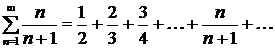 .
.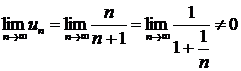 . Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.
. Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.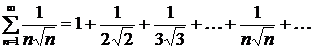 .
.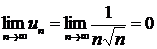 . Необходимый признак сходимости ряда выполняется.
. Необходимый признак сходимости ряда выполняется.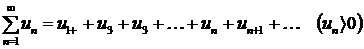 выполняется условие
выполняется условие 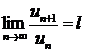 , то ряд сходится при
, то ряд сходится при 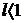 и расходится при
и расходится при 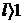 .
.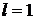 . В этом случае для исследования применяются другие приемы.
. В этом случае для исследования применяются другие приемы.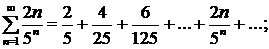
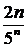 вместо n число n+1, получим
вместо n число n+1, получим 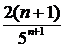 . Найдем предел отношения (n+1) –го члена к n –му члену при n
. Найдем предел отношения (n+1) –го члена к n –му члену при n 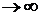 :
: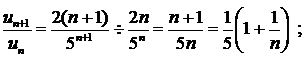
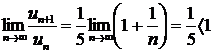 . Следовательно, данный ряд сходится.
. Следовательно, данный ряд сходится.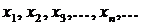 понимается функция
понимается функция 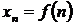 заданная на множестве
заданная на множестве 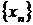 или
или 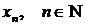 . Число
. Число 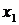 называется первым членом (элементом) последовательности,
называется первым членом (элементом) последовательности, 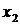 - вторым, …,
- вторым, …, 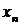 - общим или
- общим или 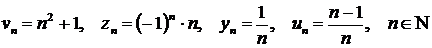
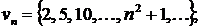
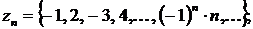
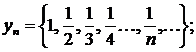
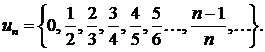
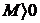 , что для любого
, что для любого 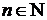 выполняется неравенство
выполняется неравенство 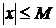 . В противном случае последовательность называется неограниченной. Легко видеть, что последовательности
. В противном случае последовательность называется неограниченной. Легко видеть, что последовательности 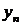 и
и 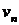 и
и 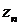 - неограниченны.
- неограниченны.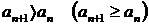 . Аналогично определяется убывающая (невозрастающая) последовательность.
. Аналогично определяется убывающая (невозрастающая) последовательность.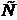 , то ее называют постоянной.
, то ее называют постоянной.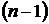 -му:
-му: 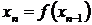 . Таким образом,
. Таким образом, 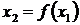 ,
, 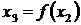 и т.д. При таком способе задания последовательности для определения
и т.д. При таком способе задания последовательности для определения 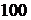 -го члена надо сначала посчитать все
-го члена надо сначала посчитать все 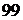 предыдущих.
предыдущих.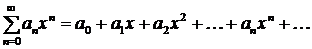 , где числа
, где числа 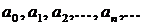 называются коэффициентами ряда, а член
называются коэффициентами ряда, а член 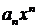 - общим членом ряда.
- общим членом ряда.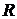 называется радиусом сходимости степенного ряда, если при
называется радиусом сходимости степенного ряда, если при 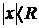 ряд сходится и при том абсолютно, а при
ряд сходится и при том абсолютно, а при 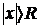 ряд расходится.
ряд расходится.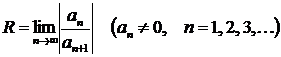 , то радиус сходимости ряда
, то радиус сходимости ряда 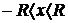 , который называется промежутком (интервалом) сходимости.
, который называется промежутком (интервалом) сходимости.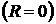 , то степенной ряд сходится в единственной точке
, то степенной ряд сходится в единственной точке 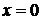 .
.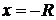 и
и 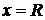 исследуется с помощью какого-либо из признаков сходимости.
исследуется с помощью какого-либо из признаков сходимости.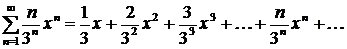 . Исследовать его сходимость в точках
. Исследовать его сходимость в точках 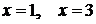 .
.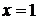 данный ряд превращается в числовой ряд
данный ряд превращается в числовой ряд 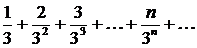 . Исследуем сходимость этого ряда по признаку Даламбера. Имеем
. Исследуем сходимость этого ряда по признаку Даламбера. Имеем 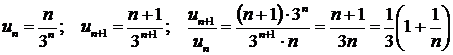 ;
;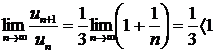 , т.е. ряд сходится.
, т.е. ряд сходится. получим ряд
получим ряд 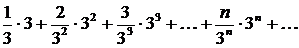 или
или 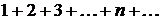 , который расходится, так как не выполняется необходимый признак сходимости ряда
, который расходится, так как не выполняется необходимый признак сходимости ряда 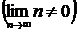 .
.


