Если для изображения действительных чисел необходима числовая прямая, то для геометрической интерпретации комплексных чисел требуется плоскость. Всякое комплексное число  можно изобразить как точку
можно изобразить как точку  на плоскости с координатами a и b (или как вектор
на плоскости с координатами a и b (или как вектор  ). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy – мнимой осью.
). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy – мнимой осью.
Изобразим на комплексной плоскости число  . Для определённости и простоты объяснений считаем, что
. Для определённости и простоты объяснений считаем, что 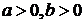 : четверти, т.е. расположим его в первой координатной (см. рис. 2.3).
: четверти, т.е. расположим его в первой координатной (см. рис. 2.3).
Рисунок 2.3. Изображение комплексного числа
Комплексное число (0, 1) обозначается символом i = (0, 1) - мнимая единица. Произведение  .
.
Эквивалентность двух приведенных определений комплексных чисел следует из того, что произвольное комплексное число z, заданное упорядоченная парой (x, y) действительных чисел x и y, можно записать в алгебраической форме: z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Определение 2.3.Модулем комплексного числа  называется расстояние от начала координат до соответствующей точки комплексной плоскости. Иначе, модуль – это длина радиус-вектора, который соединяет начала координат и соответствующую точку комплексной плоскости. Модуль комплексного числа
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Иначе, модуль – это длина радиус-вектора, который соединяет начала координат и соответствующую точку комплексной плоскости. Модуль комплексного числа  стандартно обозначают:
стандартно обозначают:  или
или  или
или  . По теореме Пифагора для
. По теореме Пифагора для  получаем формулу для нахождения модуля комплексного числа:
получаем формулу для нахождения модуля комплексного числа:  , которая справедлива для любых значений
, которая справедлива для любых значений  и
и  или
или  .
.
Определение 2.4.Аргументом комплексного числа  называется угол
называется угол  между положительной полуосью действительной оси
между положительной полуосью действительной оси 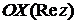 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:  .
.
Аргумент комплексного числа  стандартно обозначают:
стандартно обозначают:  или
или  . Из геометрических соображений получается следующая формула для нахождения аргумента:
. Из геометрических соображений получается следующая формула для нахождения аргумента: 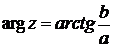 . Данная формула справедлива только в правой полуплоскости. Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.
. Данная формула справедлива только в правой полуплоскости. Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.

(Здесь функция 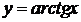 – это главный угол или дуга, тангенс которого равен
– это главный угол или дуга, тангенс которого равен 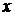 :
:  и, который изменяется в интервале
и, который изменяется в интервале  , т.е.
, т.е.  ).
).
Для  (AM=OB) получаем формулы
(AM=OB) получаем формулы  , отсюда следует, что
, отсюда следует, что  . Подставляя последние формулы в алгебраическую форму комплексного числа, получаем тригонометрическую форму записи комплексного числа:
. Подставляя последние формулы в алгебраическую форму комплексного числа, получаем тригонометрическую форму записи комплексного числа:  .
.
Умножение комплексных чисел, записанных в тригонометрической форме, выполняется стандартным образом, а далее используются тригонометрические формулы: косинус суммы и синус суммы. Получаем:

Эта формула справедлива не только для произведения 2-х комплексных чисел, но и для любого числа комплексных чисел, т.е. при умножении комплексных чисел их модули перемножаются, а их аргументы складываются.
Если перемножать  одинаковых комплексных чисел, то получается формула Муавра: формула возведения комплексного числа
одинаковых комплексных чисел, то получается формула Муавра: формула возведения комплексного числа  в степень
в степень  :
:  .
.
Для того, чтобы комплексное число возвести в степень  необходимо возвести в степень
необходимо возвести в степень  модуль этого числа, а аргумент умножить на
модуль этого числа, а аргумент умножить на  .
.



 можно изобразить как точку
можно изобразить как точку  на плоскости с координатами a и b (или как вектор
на плоскости с координатами a и b (или как вектор  ). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy – мнимой осью.
). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy – мнимой осью.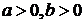 : четверти, т.е. расположим его в первой координатной (см. рис. 2.3).
: четверти, т.е. расположим его в первой координатной (см. рис. 2.3).
 .
. стандартно обозначают:
стандартно обозначают:  или
или  или
или  . По теореме Пифагора для
. По теореме Пифагора для  получаем формулу для нахождения модуля комплексного числа:
получаем формулу для нахождения модуля комплексного числа:  , которая справедлива для любых значений
, которая справедлива для любых значений  и
и  или
или  .
. между положительной полуосью действительной оси
между положительной полуосью действительной оси 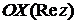 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:  .
. . Из геометрических соображений получается следующая формула для нахождения аргумента:
. Из геометрических соображений получается следующая формула для нахождения аргумента: 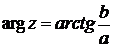 . Данная формула справедлива только в правой полуплоскости. Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.
. Данная формула справедлива только в правой полуплоскости. Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.
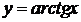 – это главный угол или дуга, тангенс которого равен
– это главный угол или дуга, тангенс которого равен 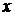 :
:  и, который изменяется в интервале
и, который изменяется в интервале  , т.е.
, т.е.  ).
). (AM=OB) получаем формулы
(AM=OB) получаем формулы  , отсюда следует, что
, отсюда следует, что  . Подставляя последние формулы в алгебраическую форму комплексного числа, получаем тригонометрическую форму записи комплексного числа:
. Подставляя последние формулы в алгебраическую форму комплексного числа, получаем тригонометрическую форму записи комплексного числа:  .
.
 одинаковых комплексных чисел, то получается формула Муавра: формула возведения комплексного числа
одинаковых комплексных чисел, то получается формула Муавра: формула возведения комплексного числа  в степень
в степень  .
.

