

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Предел числовой последовательность, его свойства и вычисление
| № | Содержание лекций | Стр. |
| 3.1. | Определение числовой последовательности | |
| 3.2. | Задание числовой последовательности | |
| 3.3. | Понятие предела числовой последовательности | |
| 3.4. | Арифметические операции над последовательностями | |
| 3.5. | Ограниченные и неограниченные последовательности | |
| 3.6. | определение подпоследовательности | |
| 3.7. | Фундаментальные последовательности | |
| 3.8. | Монотонные последовательности | |
| 3.9. | Бесконечно малые и бесконечно большие последовательности и их свойства | |
| 3.10. | Вычисление предела последовательности |
Определение числовой последовательности
Последовательность – это результат последовательного выбора элементов заданного множества. Она может быть составлена из чисел, точек, функций, векторов и т.д. Последовательность считается заданной, если указан закон, по которому каждому натуральному числу  ставится в соответствие элемент
ставится в соответствие элемент  некоторого множества. Последовательность записывается в виде
некоторого множества. Последовательность записывается в виде  , или кратко {xn}. Заметим, что числовая последовательность является функцией, область определения которой совпадает с множеством натуральных чисел, т.е. числовая последовательность – это функция натурального аргумента: xn = f(n). Элементы
, или кратко {xn}. Заметим, что числовая последовательность является функцией, область определения которой совпадает с множеством натуральных чисел, т.е. числовая последовательность – это функция натурального аргумента: xn = f(n). Элементы  называются членами последовательности,
называются членами последовательности,  - первым,
- первым,  - вторым,
- вторым,  - общим (
- общим ( -м) членом последовательности
-м) членом последовательности
Задание числовой последовательности
Аналитический способ - самый простой способ задания числовой последовательности. Это делают с помощью формулы, выражающей  -й член последовательности
-й член последовательности  через его номер
через его номер  , по которой можно вычислить любой член последовательности. Пример 3.1, если
, по которой можно вычислить любой член последовательности. Пример 3.1, если
|
|
 , то
, то  ,
,  ,
,  ,
,  .
.
Другой способ - рекуррентный (от латинского слова recurrens - «возвращающийся»), когда задают несколько первых членов последовательности и правило, позволяющее вычислять каждый следующий член через предыдущие. Пример 3.2:
 ,
,  . Можно найти
. Можно найти  ,
,  .
.
Из школьного курса известны примеры числовых последовательностей:
– арифметическая прогрессия – это такая числовая последовательность, в которой каждый член равен предыдущему, сложенному с постоянным для данной последовательности числом:  ; формула общего члена:
; формула общего члена:  , где
, где  – первый член, а
– первый член, а  – разность прогрессии.
– разность прогрессии.
– геометрическая прогрессия – это такая числовая последовательность, в которой каждый член равен предыдущему, умноженному на постоянным для данной последовательности число:  ; формула общего члена:
; формула общего члена:  , где
, где 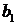 – первый член, а
– первый член, а  – знаменатель прогрессии.
– знаменатель прогрессии.
Теорема.
Если последовательность { xn } сходится и ее предел равен a, то любая ее подпоследовательность также сходится и имеет тот же самый предел.
Если { xn } – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая.
Фундаментальные последовательности
Определение.
1. Последовательность 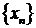 возрастает, если
возрастает, если 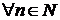

xn<  : каждый член последовательности меньше последующего;
: каждый член последовательности меньше последующего;
2. Последовательность 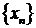 убывает, если
убывает, если 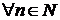

(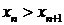 ): каждый член последовательности больше последующего;
): каждый член последовательности больше последующего;
3. Последовательность 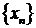 не возрастает, если
не возрастает, если 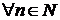

 : каждый член последовательности не меньше последующего;
: каждый член последовательности не меньше последующего;
4. Последовательность 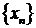 не убывает, если
не убывает, если 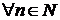

( ): каждый член последовательности не больше последующего;
): каждый член последовательности не больше последующего;
5. Последовательность 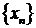 называется монотонной, если она является или возрастающей, или убывающей, или не возрастающей, или не убывающей.
называется монотонной, если она является или возрастающей, или убывающей, или не возрастающей, или не убывающей.
6. У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.
7. Предел последовательности, все члены которой равны числу  , равен
, равен  .
.
|
|
8. Теорема 13. Если монотонная последовательность  ограничена, то она сходится.
ограничена, то она сходится.
Доказательство. Так как последовательность  ограничена, то множество ее элементов имеет точные верхнюю
ограничена, то множество ее элементов имеет точные верхнюю  и нижнюю
и нижнюю  грани. Пусть
грани. Пусть  – неубывающая последовательность и
– неубывающая последовательность и  – точная верхняя грань множества ее элементов. Это означает, что для любого числа
– точная верхняя грань множества ее элементов. Это означает, что для любого числа 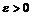 можно указать такой элемент
можно указать такой элемент  , что
, что  и
и 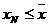 . Эти два неравенства равносильны неравенству
. Эти два неравенства равносильны неравенству  или
или  . Так как
. Так как  – неубывающая последовательность, то при
– неубывающая последовательность, то при  выполняется
выполняется  или
или  . Это означает, что при
. Это означает, что при  выполняется
выполняется  или
или  . Таким образом,
. Таким образом,  . Аналогично доказывается случай, когда
. Аналогично доказывается случай, когда  – невозрастающая последовательность.
– невозрастающая последовательность.
Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме 8 сходящаяся монотонная последовательность ограничена.
Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность  сходится к числу ноль, но не является монотонной.
сходится к числу ноль, но не является монотонной.
Замечание 3. Если последовательность  неубывающая сходящаяся и
неубывающая сходящаяся и  - ее предел, то для всех номеров n выполняется неравенство
- ее предел, то для всех номеров n выполняется неравенство 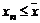 . Аналогично, если
. Аналогично, если  невозрастающая сходящаяся последовательность и
невозрастающая сходящаяся последовательность и  – ее предел, то для всех номеров n справедливо
– ее предел, то для всех номеров n справедливо 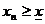 .
.
Теорема 13 (теорема Больцано-Вейерштрасса). Из всякой ограниченной последовательности действительных чисел, можно выделить сходящуюся подпоследовательность.
.
Теорема (Вейерштрасс). Любая монотонная ограниченная последовательность имеет предел.
Доказательство. Докажем теорему для монотонной возрастающей последовательности  . Докажем, что точная верхняя граница для последовательности
. Докажем, что точная верхняя граница для последовательности 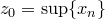 и будет ее пределом.
и будет ее пределом.
Действительно, по определению точной верхней границы

Кроме того, какое бы ни взять число  , найдется такой номер
, найдется такой номер 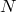 , что
, что

Так как последовательность монотонна, то при  будет
будет  , а значит, и
, а значит, и  и выполняются неравенства
и выполняются неравенства
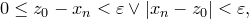
откуда и следует, что 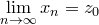 .
.
Эта замечательная теорема дает достаточные условия существования предела. Из нее, например, следует, что последовательность площадей правильных  -угольников, вписанных в окружность единичного радиуса, имеет предел, так как является монотонно возрастающей и ограниченной сверху. Предел этой последовательности обозначается
-угольников, вписанных в окружность единичного радиуса, имеет предел, так как является монотонно возрастающей и ограниченной сверху. Предел этой последовательности обозначается  .
.
С помощью предела монотонной ограниченной последовательности определяется играющее большую роль в математическом анализе число  - основание натуральных логарифмов:
- основание натуральных логарифмов:
|
|
 . Некоторые замечательные пределы.
. Некоторые замечательные пределы. 
Предел числовой последовательность, его свойства и вычисление
| № | Содержание лекций | Стр. |
| 3.1. | Определение числовой последовательности | |
| 3.2. | Задание числовой последовательности | |
| 3.3. | Понятие предела числовой последовательности | |
| 3.4. | Арифметические операции над последовательностями | |
| 3.5. | Ограниченные и неограниченные последовательности | |
| 3.6. | определение подпоследовательности | |
| 3.7. | Фундаментальные последовательности | |
| 3.8. | Монотонные последовательности | |
| 3.9. | Бесконечно малые и бесконечно большие последовательности и их свойства | |
| 3.10. | Вычисление предела последовательности |
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!