Пример 1:Постройте график функции  .
Решение. 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем .
Решение. 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем  : :
 = =  = =  . Видим, что . Видим, что  и и  , следовательно, функция , следовательно, функция  ни четная, ни нечетная.
3. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у =0. Получим уравнение: ни четная, ни нечетная.
3. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у =0. Получим уравнение:  . Итак, точка (0; 0) – точка пересечения с осями координат.
4. Найдем производную функции по правилу дифференцирования дроби: . Итак, точка (0; 0) – точка пересечения с осями координат.
4. Найдем производную функции по правилу дифференцирования дроби:  = =  = =  = = 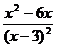 = =  .
5. Для нахождения критических точек первого рода найдем точки, в которых производная функции равна 0 или не существует. .
5. Для нахождения критических точек первого рода найдем точки, в которых производная функции равна 0 или не существует.
 , если , если  =0, следовательно, =0, следовательно,  . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: 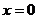 или или 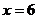 . .
 не существует, если знаменатель (х -3)2 равен 0, т.е. не существует, если знаменатель (х -3)2 равен 0, т.е.  не существует при х =3.
Итак, функция имеет три критические точки первого рода: не существует при х =3.
Итак, функция имеет три критические точки первого рода:  ; ;  ; ;  .
На числовой оси отметим критические точки первого рода, причем точку .
На числовой оси отметим критические точки первого рода, причем точку  отмечаем выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки производной отмечаем выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки производной  = =  на каждом промежутке: на каждом промежутке:

На промежутках, где 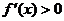 , исходная функция возрастает (при , исходная функция возрастает (при  (-∞;0] (-∞;0]  ), где ), где  - убывает (при - убывает (при  [0;3) [0;3)  (3;6]). (3;6]).
Точка х =0 является точкой максимума функции..
Точка х =6 является точкой минимума функции.
6. Найдем вторую производную функции как производную от первой производной:   = =  = =
=  . .
Вынесем в числителе х -3 за скобки и выполним сокращение:
  = =  . .
Приведем в числителе подобные слагаемые:   . .
7. Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.
 0, если 0, если  =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет. =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.
 не существует, если знаменатель (х -3)3 равен 0, т.е. не существует, если знаменатель (х -3)3 равен 0, т.е.  не существует при х =3. не существует при х =3.
Итак, функция имеет одну критическую точку второго рода:  . .
Найдем интервалы выпуклости и точки перегиба графика функции.
На числовой оси отметим критическую точку второго рода выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки второй производной   на каждом промежутке: на каждом промежутке:

На промежутках, где  , исходная функция вогнута (при , исходная функция вогнута (при  (3;+∞)), где (3;+∞)), где  - выпукла (при - выпукла (при  (-∞;3)). (-∞;3)).
Точка х =3 не является точкой перегиба графика функции, т.к. в ней исходная функция не определена.
8. Найдем асимптоты графика функции.
8.1. Поскольку область определения функции – все действительные числа за исключением х =3, то проверим, является ли прямая х= 3 вертикальной асимптотой. Для этого вычислим предел функции  в точке х= 3: в точке х= 3: 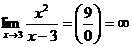 . .
Получили, что  , следовательно, х= 3 - вертикальная асимптота. , следовательно, х= 3 - вертикальная асимптота.
8.2. Для поиска горизонтальных асимптот находим  : :
b =  . Т.к. b – бесконечность, то горизонтальных асимптот нет. . Т.к. b – бесконечность, то горизонтальных асимптот нет.
8.3. Для поиска наклонных асимптот находим 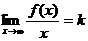 : :
  = =  = =  =1. =1.
Итак,  1. Найдем b по формуле: 1. Найдем b по формуле:  . .
b=  = =  = =  = =  . .
Получили, что b= 3. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+3.
Таким образом, данная функция имеет вертикальную асимптоту х= 3 и наклонную асимптоту у=x+3.
 9. 9.
| х
| -1
|
|
|
|
|
|
| | у
| -0,3
|
| -0,5
| -
|
|
| 12,8
| |
|
| т.max
|
| Верт.
асим.
|
| т.min
|
|  , ,  , , 
  
10. По результатам исследования и точкам строим график функции.
|



 - функция чётная (симметрия относительно ОУ)
- функция чётная (симметрия относительно ОУ)
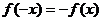 - функция нечётная (симметрия относительно начала координат)
- функция нечётная (симметрия относительно начала координат)
 - функция общего вида (симметрии нет)
- функция общего вида (симметрии нет)
 (найти корни уравнения, отметить их на прямой, разбить на промежутки)
2)определить знак производной в каждом интервале(подставить удобное число в производную),
3) сделать вывод
(найти корни уравнения, отметить их на прямой, разбить на промежутки)
2)определить знак производной в каждом интервале(подставить удобное число в производную),
3) сделать вывод
 (найти корни уравнения, отметить их на прямой, разбить на промежутки)
2)определить знак производной в каждом интервале(подставить удобное число во вторую производную),
3) сделать вывод
(найти корни уравнения, отметить их на прямой, разбить на промежутки)
2)определить знак производной в каждом интервале(подставить удобное число во вторую производную),
3) сделать вывод
 .
Решение. 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем
.
Решение. 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем  :
:
 =
=  =
=  . Видим, что
. Видим, что  и
и  , следовательно, функция
, следовательно, функция  . Итак, точка (0; 0) – точка пересечения с осями координат.
4. Найдем производную функции по правилу дифференцирования дроби:
. Итак, точка (0; 0) – точка пересечения с осями координат.
4. Найдем производную функции по правилу дифференцирования дроби:  =
=  =
=  =
= 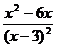 =
=  .
5. Для нахождения критических точек первого рода найдем точки, в которых производная функции равна 0 или не существует.
.
5. Для нахождения критических точек первого рода найдем точки, в которых производная функции равна 0 или не существует.
 , если
, если  . Произведение тогда равно 0, когда хотя бы один из множителей равен 0:
. Произведение тогда равно 0, когда хотя бы один из множителей равен 0: 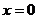 или
или 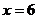 .
.
 не существует, если знаменатель (х -3)2 равен 0, т.е.
не существует, если знаменатель (х -3)2 равен 0, т.е.  ;
;  ;
;  .
На числовой оси отметим критические точки первого рода, причем точку
.
На числовой оси отметим критические точки первого рода, причем точку 
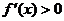 , исходная функция возрастает (при
, исходная функция возрастает (при  (-∞;0]
(-∞;0]  ), где
), где  - убывает (при
- убывает (при  (3;6]).
(3;6]).
 =
=  =
= .
. =
=  .
. .
. не существует, если знаменатель (х -3)3 равен 0, т.е.
не существует, если знаменатель (х -3)3 равен 0, т.е.  .
.
 , исходная функция вогнута (при
, исходная функция вогнута (при  - выпукла (при
- выпукла (при 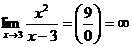 .
. , следовательно, х= 3 - вертикальная асимптота.
, следовательно, х= 3 - вертикальная асимптота. :
: . Т.к. b – бесконечность, то горизонтальных асимптот нет.
. Т.к. b – бесконечность, то горизонтальных асимптот нет.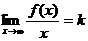 :
:
 =
=  =
=  =1.
=1. .
. =
=  =
=  =
=  .
. 9.
9. ,
,  ,
, 






