3. Решить сравнение: 6х º 4 (mod 8).
Решение.
Так как здесь (6; 8) = d = 2 и 4  2, то сравнение имеет d = 2 классов решений по модулю 8 или 1 класс решений по модулю т: d = 8: 2, т.е. по модулю 4.
2, то сравнение имеет d = 2 классов решений по модулю 8 или 1 класс решений по модулю т: d = 8: 2, т.е. по модулю 4.
1) Разделим обе части сравнения и модуль на число 2, получим: 3х º 2 (mod 4). Здесь (3; 4) = 1, поэтому сравнение имеет один класс решений по модулю 4:
3х º 2 + 4 (mod 4) Þ 3х º 6(mod 4). Так как (3; 4) = 1, то обе части сравнения разделим на 3. Тогда х º 2 (mod 4) – получили 1 класс решений по модулю 4. Запишем этот класс так: x = 2 + 4q, qÎZ. Дадим параметру q два значения (так как d = 2): q = 0 и q = 1. При q = 0 x1 º 2(mod 8); при q = 1 x2 º 6(mod 8) – получили два класса решений по начальному модулю 8.
Ответ: х º2(mod4) или x º 2; 6 (mod 8).
4. Решить в целых числах неопределённое уравнение 5х – 9у = 7.
Решение.
1) 5х – 7 = 9у Þ (5х – 7)  9 Þ 5х º 7(mod 9) Þ 5х º 7 + 2×9 º 25 (mod 9) Þ
9 Þ 5х º 7(mod 9) Þ 5х º 7 + 2×9 º 25 (mod 9) Þ
Þ х º 5(mod 9), откуда х = 5 + 9q, qÎZ.
2) Подставим это выражение для х в данное уравнение:
 Þ
Þ  Þ
Þ  (q Î Z) –бесконечное множество решений.
(q Î Z) –бесконечное множество решений.
Ответ: (5; 2), (14; 7), (23; 17) и так далее.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Определите, имеет ли решение данное сравнение; если решение есть, то установите, сколько классов вычетов (сколько решений) имеет данное сравнение.
173. 3 х º 5 (mod 8). 174. 9 х º 3 (mod 16). 175. 9 х º 15 (mod 27).
176. 15 х º 24 (mod 21). 177. 15 х º 24 (mod 25). 178. 15 х º 10 (mod 25). 179. 25 х º 15 (mod 50). 180. 50 х º 20 (mod 10). 181. 63 х º 42 (mod 210).
182. 100 х º 25 (mod 200). 183. 10 х º 2 (mod 24). 184. 36 х º 24 (mod 25).
Решите сравнения способом перебора соответствующих классов вычетов.
185. 2 х º 1 (mod 3). 186. 3 х º 5 (mod 4). 187. 3 х º 2 (mod 6). 188. 2 х º 3(mod7).
189. 4 х º 2 (mod 6). 190. 4 х º 1 (mod 5). 191. 3 х º 0 (mod 9). 192. 6 х º9(mod10).
Решите сравнения, используя теоремы равносильности сравнений.
193. 5 х º 8 (mod 12). 194. 7 х º – 3 (mod 17). 195. 8 х º 13 (mod 9). 196. 37 х 2 + 9 х – 1 º 0 (mod 37). 197. 54 х º 3 (mod 37). 198. 27 х º – 21(mod29).
199. 58 х 3 –29 х 2+21 х º – 5(mod29).200. 35 х º 4 (mod 39). 201.32 х 4+23 х º–41(mod32)
Установите, имеет ли решение данное сравнение, и если имеет, то найдите это решение.
202. 2 х º 5 (mod 3). 203. 3 х º 4 (mod 5). 204. 5 х º 2 (mod 8).
205. 7 х º 1 (mod 12). 206. 4 х º – 2 (mod15). 207. 4 х º 3 (mod 8).
208. 5 х º 8 (mod 7). 209. 17 х º 11 (mod 7). 210. 11 х º 2 (mod 12).
211. 18 х º 9 (mod 8). 212. 18 х º 12 (mod 6). 213. 18 х º 10 (mod 4).
214. 6 х º 9 (mod 3). 215. 6 х º 9 (mod 12). 216. 6 х º 3 (mod 9).
217. 8 х º 20 (mod 12). 218. 12 х º 15 (mod 21). 219. 45 х º 31 (mod 100).
220. 7 х º 2 (mod 13). 221. 17 х º 50 (mod 9). 222.140 х +36º8–3 х (mod15)
223. 72 х º 2 (mod 10). 224. 29 х º 1 (mod 17). 225. 7 х º 15 (mod 9).
226. 12 х º 24 (mod 16). 227. 8 х º 27 (mod 12). 228. 10 х º 15 (mod 35).
229. 17 х º 47 (mod 78). 230. 19 х º 15 (mod 70). 231. 15 х º 13 (mod 64). 232. 94 х º 8 (mod 58). 233. 43 х º 51 (mod 12). 234. 16 х º 8 (mod 20).
Решите неопределённые уравнения первой степени с двумя неизвестными на множестве целых чисел Z с помощью перехода к соответствующим сравнениям:
235. 4 x – 3 y = 2. 236. 17 x + 13 y = 1. 237. 2 x – 4 y = 7. 238. 5 x + 4 y = 3. 239. 6 x – 25 y = 4. 240. 6 x + 9 y = 8. 241. 17 x – 12 y = 27.
242. 15 x – 17 y = – 42. 243. 8 x – 15 y = 18. 244. 13 x – 19 y = 18.
СИСТЕМЫ ЛИНЕЙНЫХ СРАВНЕНИЙ С ОДНОЙ НЕИЗВЕСТНОЙ
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
14. 1. Определение 1.
| Системой линейных сравнений с одной неизвестной называется система вида
|

|
где аi, bi., xÎ Z, тi Î N. тi >1,
(*) ai не  тi (i = 1, 2,..., s). тi (i = 1, 2,..., s).
|
14. 2. Определение 2.
Решением системы (*) называется класс вычетов, удовлетворяющий каждому сравнению этой системы.
Если система (*) имеет хотя бы один класс решений, то она называется
совместной (и в противном случае – несовместной).
14. 3. Следствие 1.
Если хотя бы одно из сравнений системы (*) не имеет решений, то и вся система (*) не имеет решений (то есть несовместна).
14. 4. Теорема 1.
| Рассмотрим систему (**)– частный случай системы (*):
|
 (**) (**)
| Пусть НОД(т 1; т 2) = (т 1; т 2) = d,
НОК (т 1; т 2) = [ т 1; т 2] = m.
|
Тогда: 1) если (b 2 – b 1) не  d, то система (**) не имеет решений;
2) если (b 2 – b 1) d, то система (**) не имеет решений;
2) если (b 2 – b 1)  d, то система (**) имеет 1 класс решений по модулю [ т 1; т 2] = m. d, то система (**) имеет 1 класс решений по модулю [ т 1; т 2] = m.
|
14. 5. Следствие 2.
Если (т 1; т 2) = d = 1, – то т = т 1 × т 2 и система (**) совместна и имеет один класс решений по модулю т = т 1 × т 2.
Заметим, что теорема 1 может быть обобщена на случай, когда система (**) содер- жит произвольное (конечное) число сравнений вида x º bj (mod m j).
В частности, если т 1, т 2, …, т s – взаимно простые числа, то система (**) всегда совместна и имеет 1 класс решений по модулю т 1 × т 2 × … × т s.
14. 6. Вернёмся к рассмотрению системы сравнений (*) вида ai x º bj ( mod m j ).
1) Обозначим (ai ; mi) = di (i = 1,..., s). Если хотя бы при одном значении i bi не  di,то i -е сравнение системы не имеет решений, а, значит, и вся система (*) несовместна.
di,то i -е сравнение системы не имеет решений, а, значит, и вся система (*) несовместна.
2) Если же bi  di для всех i, то каждое сравнение системы (*) можно решить относительно x и заменить систему (*) равносильной системой (***):
di для всех i, то каждое сравнение системы (*) можно решить относительно x и заменить систему (*) равносильной системой (***):
 (***) (***)
|
Эта система либо несовместна, либо имеет 1 класс решений по модулю [ m 1: d 1,..., m s: d s].
|
14. 7. Линейные сравнения по составному модулю вида ax º b ( mod p 1 × р 2 ).
Так как (ах – b)  (р 1 × р 2), то
(р 1 × р 2), то  Þ
Þ 
ТИПОВЫЕ ЗАДАЧИ
1. Имеют ли решения системы: 1)  2)
2)  ?
?
Решение.
1) Здесь (т 1; т 2) = (9;6)= d =3, b 2 – b 1= 8–5=3.Так как 3  3, то система совместна.
3, то система совместна.
2) Здесь (т 1; т 2) = (9;6)= d =3, b 2 – b 1= 3–1=2.Так как 2 не  3, то система несовместна.
3, то система несовместна.
2. Решить систему: 
Решение.
1) Выразим х из первого сравнения и подставим во второе:
 Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ
Þ 
2) Подставим t в 1-е сравнение: x = 3 + 15(1+ 8 q) Þ x = 18+120 q или х º 18(mod120).
3. Решить систему:  (Здесь т = [7; 9; 15] = 7 ×9 ×5 = 315).
(Здесь т = [7; 9; 15] = 7 ×9 ×5 = 315).
Решение.
1) Из (1) x = 2 + 7 t, подставим в (2):
 Þ
Þ  Þ
Þ  Þ
Þ  Þ Þ
Þ Þ  Þ
Þ 
2) Подставим х из (4) в (3):
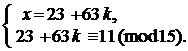 Þ
Þ  Þ
Þ  Þ
Þ
Þ  Þ
Þ  Þ х = 23 + 63 (1 + 5 q) Þ x = 86 + 315 q.
Þ х = 23 + 63 (1 + 5 q) Þ x = 86 + 315 q.
Ответ: х º 86 (mod 315).
4. Решить систему:  (Здесь т = [11; 35; 5] = 11×35 = 385).
(Здесь т = [11; 35; 5] = 11×35 = 385).
Решение.
Упростим данные сравнения и решим каждое из них (это возможно – проверьте!).
 Þ
Þ 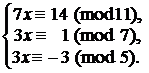 Þ
Þ  Þ
Þ 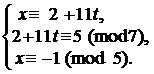 Þ
Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ
Þ  Þ
Þ  Þ х = – 9 + 77 (– 1 + 5 q) Þ х = – 86 + 385 q.
Þ х = – 9 + 77 (– 1 + 5 q) Þ х = – 86 + 385 q.
Ответ: х º – 86 (mod 385).
5. Решить линейное сравнение по составному модулю: 5 х º 8 (mod 21).
Решение.
Так как здесь модуль 21 = 7×3, то сравнение равносильно системе  Þ
Þ
Þ  Þ
Þ  Þ
Þ  откуда х = 3 + 7(1 + 3 q) Þ
откуда х = 3 + 7(1 + 3 q) Þ
Þ х = 10 + 21 q, или х º 10 (mod 21).
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Установите, совместна ли данная система сравнений; если она совместна, то определите, по какому модулю должны быть получены решения системы, а затем найдите эти решения.
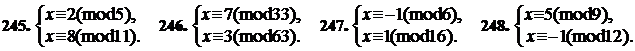
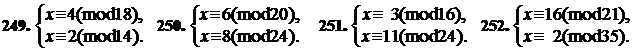
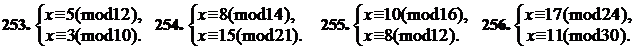
Решите системы сравнений:
257.  258.
258.  259.
259.  260.
260. 






Глава 5. КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
§ 16. ПОНЯТИЕ КОНЕЧНОЙ ЦЕПНОЙ ДРОБИ
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
16. 1. Определение 1.
| Конечной цепной дробью называется число Ап вида
|
Ап =  , ,
| где а 0Î Z,
аi Î N (i = 1, 2,..., n), аn ¹ 1,
n – длина цепной дроби.
Обозначение: 
|
Пример конечной цепной дроби: Ап =  = [4; 3, 1, 2], где n = 3.
= [4; 3, 1, 2], где n = 3.
16. 2. Отметим, что: 1) всякая конечная цепная дробь преобразуется в рациональное
число вида 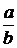 .
.
Например: А 3 = [4; 3, 1, 2] =  .
.
2) обратно: всякое рациональное число вида 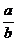 может быть представлено в виде конечной цепной дроби, причём единственным образом..
может быть представлено в виде конечной цепной дроби, причём единственным образом..
16. 3. Алгоритм преобразования несократимой дроби  в конечную цепную дробь.
в конечную цепную дробь.
Пример. Дробь  =
=  преобразовать в конечную цепную дробь.
преобразовать в конечную цепную дробь.
Решение.
1) Делим числитель 47 на знаменатель 11, остаток r1 = 3;
2) делим знаменатель 11 на 1-й остаток, r1 = 3;
3) делим 1-й остаток r1 = 3 на 2-й остаток, r2 = 2;
4) делим 2-й остаток r2 = 2 на 3-й остаток, r3 = 1;
5) выписываем частные а 0 = 4, а 1 = 3, а 2 = 1, а 3 = 2.
Ответ: дробь 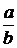 = =  = [4; 3, 1, 2], где n = 3. = [4; 3, 1, 2], где n = 3.
| 47 | 11_
44 4 = а0
11 | 3 = r1
9 3 = a1
3 | 2 = r2
2 1 = a2
2 | 1 = r3
2 2 = a3
0
|
16. 4. Рассмотрим конечные цепные дроби:
 = А 3 = [4; 3, 1, 2] =
= А 3 = [4; 3, 1, 2] =  = 4
= 4  ; А 2 = [4; 3, 1] = 4
; А 2 = [4; 3, 1] = 4  ; А 1 = [4;3] = 4
; А 1 = [4;3] = 4  ; А 0 = [4] = 4.
; А 0 = [4] = 4.

| Числа последовательности А 0, А 1, А 2, А 3,… всё ближе подходят к данному числу Ап = а/b. Причём Аi с чётными номерами – слева от Ап,
Aj с нечётными номерами – справа от Ап.
|
В общем случае:

| Последовательность А 0, А 2, А 4 ,…возрастает,
Последовательность А 1, А 3, А 5 ,… убывает; члены каждой последовательности всё ближе подходят к исходному числу Ап = а/b.
|
| 16. 5. Определение 2.
Подходящей дробью k -го порядка данной конечной цепной дроби Ап = а/b
называется конечная цепная дробь Аk = [ a 0; a 1, a 2, …, a k] (k £ n), полученная из данной цепной дроби Аn = [ a 0; a 1, a 2, …, a k, …, a n] отбрасыванием последних n – k чисел.
|
Пусть  – несократимая дробь. Если
– несократимая дробь. Если  = Аn = [ a 0; a 1, a 2, …, a n], то
= Аn = [ a 0; a 1, a 2, …, a n], то
А 0 = [ a 0] – подходящая дробь 0-го порядка;
А 1 = [ a 0; a 1] – подходящая дробь 1-го порядка;
А 2 = [ a 0; a 1, a 2] – подходящая дробь 2-го порядка;
................................................
А n = [ a 0; a 1, a 2, …, a n] – подходящая дробь п -го порядка.
Обозначение k-й подходящей дроби:  , где Pk – числитель k-й подходящей дроби,
, где Pk – числитель k-й подходящей дроби,
Qk – знаменатель k-й подходящей дроби.
16. 6. Алгоритм вычисления Pk и Qk.
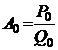 = [ a 0] Þ P 0 = а 0; Q 0 = 1.
= [ a 0] Þ P 0 = а 0; Q 0 = 1.
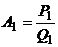 = [ a 0; a 1] Þ P 1 = а 1 × P 0 + 1; Q 1 = а 1.
= [ a 0; a 1] Þ P 1 = а 1 × P 0 + 1; Q 1 = а 1.
 = [ a 0; a 1, а 2] Þ P 2 = а 2 × P 1 + P 0; Q 2 = а 2 × Q 1 + Q 0.
= [ a 0; a 1, а 2] Þ P 2 = а 2 × P 1 + P 0; Q 2 = а 2 × Q 1 + Q 0.
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
 = [ a 0; a 1, а 2 , …, ak ] Þ Pk = аk × Pk – 1 + Pk – 2; Qk = аk × Qk – 1 + Qk – 2
= [ a 0; a 1, а 2 , …, ak ] Þ Pk = аk × Pk – 1 + Pk – 2; Qk = аk × Qk – 1 + Qk – 2
и так далее.
Пример, демонстрирующий технику нахождения Pk и Qk.
Для данной конечной цепной дроби А 3 = [4; 3, 1, 2] составьте все подходящие дроби.
Решение.

P 0= a 0=4, P 1=4×3+1=13, P 2=1×13+4=17, P 3= 2×17+13=47.
Q 0= 1, Q 1= a 1=3, Q 2=1×3+1= 4, Q 3 = 2×4 + 3 = 11.
Ответ: подходящие дроби А 0 = 4/1, А 1 = 13/3, А 2 = 17/4, А 3 = 47/11 = а / b.
ТИПОВЫЕ ЗАДАЧИ
1. Преобразовать конечную цепную дробь А 4 = [4; 1, 1, 3, 12] в число вида  .
.
Решение.
А 4 = [4; 1, 1, 3, 12] =  .
.
2. Преобразовать данную дробь вида  в конечную цепную дробь: а)
в конечную цепную дробь: а) 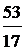 ; б)
; б)  ; в)
; в)  .
.
Решение.
| а) 53 | 17_
51 3
17 | 2
16 8
2 | 1
2 2
| б) 26 | 11_
22 2
11 | 4
8 2
4 | 3
3 1
3 | 1
3 3
0
| в) 916 | 171_
855 5
171 | 61_
122 2
61 | 49
49 1
49 | 12
48 4
12 | 1_
12 12
|
Ответ: а)  = [3; 8, 2]; б)
= [3; 8, 2]; б)  = [2; 2, 1, 3]; в)
= [2; 2, 1, 3]; в)  = [5; 2, 1, 4, 12].
= [5; 2, 1, 4, 12].
3. Для данной конечной цепной дроби составить все подходящие дроби:
а) А 3 = [3; 2, 1, 2]; б) А 4 = [4; 1, 1, 3, 12].
Решение.
| а) k
| 0 1 2 3
|
| б) k
| 0 1 2 3 4
| Ответ:
а) А 0 =  ; А 1 = ; А 1 =  ; А 2 = ; А 2 =  ; А 3 = ; А 3 =  ;
б) А 0 = ;
б) А 0 =  ; А 1 = ; А 1 =  ; А 2 = ; А 2 =  ; А 3 = ; А 3 =  ; А 4 = ; А 4 =  . .
|
| ak
| 3 2 1 2
| ak
| 4 1 1 3 12
|
| Pk
Qk
| 3 7 10 27
1 2 3 8
| Pk
Qk
| 4 5 9 32 393
1 1 2 7 86
|
Проверка: 
| Проверка: 
|
.4. Для данной цепной дроби Ап найти числитель Pп – 1 и знаменатель Qп – 1 предпоследней подходящей дроби: а) А 3 = [5; 2, 3, 1]; б) А 4 = [2; 1, 1, 2, 4]. Сделать проверку.
Решение.
| а) k
| 0 1 2 3
|
| б) k
| 0 1 2 3 4
| Проверка::
а) А 2 = 5 +  ;
б) А 3 = ;
б) А 3 =  . .
|
| ak
| 5 2 3 1
| ak
| 2 1 1 2 4
|
| Pk
Qk
| 5 11 38
1 2 7
| Pk
Qk
| 2 3 5 13
1 1 2 5
|
| Ответ:
P 2 = 38, Q 2 = 7;
| Ответ:
P 3 = 13, Q 3 = 5.
|
5. С помощью подходящих дробей сократите дроби: а)  ; б)
; б)  .
.
Решение.
Преобразуем данную дробь в цепную дробь и составим п -ю подходящую дробь Ап.
Тогда получившаяся подходящая дробь Ап совпадёт с видом сокращённой заданной дроби.
а) 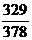 = [0; 1, 6, 1, 2, 2] = [0; 1, 6, 1, 2, 2]
|
| б)  = [2; 8, 1, 2] = [2; 8, 1, 2]
| Ответ:
а)  = =  ;
б) ;
б)  = =  . .
|
| ak
| 0 1 6 1 2 2
| ak
| 2 8 1 2
|
| Pk
Qk
| 0 1 6 7 20 47
1 1 7 8 23 54
| Pk
Qk
| 2 17 19 55
1 8 9 26
|
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
306. Данную конечную цепную дробь преобразуйте в рациональное число вида 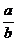 :
:
а) А 3 =  ; б) А 3 = [2; 2, 1, 5]; в) А 3 = [3; 11, 2, 4]; г) А 4 = [– 2; 1, 2, 1, 2].
; б) А 3 = [2; 2, 1, 5]; в) А 3 = [3; 11, 2, 4]; г) А 4 = [– 2; 1, 2, 1, 2].
307. Данное рациональное число вида 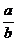 преобразуйте в конечную цепную дробь:
преобразуйте в конечную цепную дробь:
а) 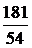 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
308. Для данной конечной цепной дроби составьте все подходящие дроби:
а) А 3 = [ 4; 2, 1, 3]; б) А 4 = [3; 2, 1, 5, 3]; в) А 6 = [1; 3, 4, 1, 2, 1, 3];
г) А 3 = [0; 3, 3, 2]; д) А 3 = [– 4; 1, 3, 2].
309. Для данной конечной цепной дроби составьте Pn – 1 и Qn – 1 – числитель и знаменатель предпоследней подходящей дроби:
а) А 3 = [ 5; 1, 3, 2]; б) А 4 = [1; 2, 3, 4, 5]; в) А 3 = [– 3; 2, 1, 4]; г) А 3 = [ 0; 4, 3, 2].
310. Для данной дроби 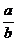 найдите предпоследнюю подходящую дробь:
найдите предпоследнюю подходящую дробь:
а)  =
=  ; б)
; б)  =
=  ; в)
; в)  =
=  ; г)
; г)  =
=  ; д)
; д)  =
=  .
.
311. Сократите данную дробь (если это возможно), с помощью подходящих дробей:
а)  =
=  ; б)
; б)  =
=  ; в)
; в)  =
=  ; г)
; г)  =
=  ; д)
; д)  =
=  ; е)
; е)  =
=  .
.
§ 17. РЕШЕНИЕ СРАВНЕНИЙ ВИДА ах º b (mod m)
С ПОМОЩЬЮ КОНЕЧНЫХ ЦЕПНЫХ ДРОБЕЙ
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
17. 1. Алгоритм решения сравнений ах º b (mod m), где (а; т) = 1 (18)
В этом случае сравнение (18) имеет 1 класс решений. Для его нахождения нужно:
1) составить дробь  и преобразовать её в конечную цепную дробь:
и преобразовать её в конечную цепную дробь:  = [ a 0; a 1, a 2,…, an ]
= [ a 0; a 1, a 2,…, an ]
2) найти числитель Pп – 1 предпоследней подходящей дроби;
3) применить формулу х º (– 1) п × b × Рп – 1 (mod m) (19)
(см. ниже, типовые задачи, пример 1).
17. 2. Алгоритм решения сравнений ах º b (mod m), где (а; т) = d >1, b  d (20)
d (20)
В этом случае сравнение (20) имеет d классов решений по модулю т. Для их нахождения нужно:
1) сократить a, b и m на число d и получить сравнение (а: d ) x º b: d (mod ( m: d )) (*)
(чùсла а: d, b: d, m: d – целые!);
2) по алгоритму из пункта 17. 1 решить сравнение (*), имеющее один класс решений по mod (m: d). Получим: x º х 0 (mod ( m: d )), или x = х 0 + ( m: d ) × t, где t Î Z.
3) полагая число t = 0, 1, 2, …, d – 1, получим d классов решений сравнения (20) по модулю m: x º х 0; х 0 + (m: d) ×1; х 0 + (m: d) ×2; …; х 0 + (m: d) × (d – 1) (mod m) (см. ниже, типовые задачи, пример 2).
17. 3. Напомним, что сравнение ах º b (mod m), где (а; т) = d > 1, b не  d, – не имеет решений.
d, – не имеет решений.
ТИПОВЫЕ ЗАДАЧИ
1. С помощью конечных цепных дробей решить сравнение 171 x º3(mod916).
Решение. (См. выше – алгоритм решения – в пункте 17. 1).
1) Так как (171;916) = 1 (проверьте!), то сравнение имеет 1 класс решений. Найдём его.
2) Составим дробь  =
=  и преобразуем её в цепную дробь:
и преобразуем её в цепную дробь:  =
=  =[5; 2, 1, 4, 12]
=[5; 2, 1, 4, 12]
(см. § 16, типовые задачи, пример 2, в)).
3) Найдём Pn – 1 – числитель предпоследней подходящей дроби (для проверки вычис-
| лений найдём и Pn ):
| ak
| 5 2 1 4 12
| Pn – 1 = 75.
|
| Pk
| 5 11 16 75 916
|
4) Воспользуемся формулой (24) (при п = 4, b = 3, Pn – 1 = 75, т = 916):
х º (– 1) 4 ×3× 75 (mod916) Þ х º 225 (mod916).
2. С помощью конечных цепных дробей решить сравнение: 42 x º57(mod75).
Решение. (См. выше – алгоритм решения – в пункте 17. 2).
1) Так как (42;75) = d =3 (проверьте!) и 57  3, то сравнение имеет 3 класса решений. Сократив a, b и т на d =3, получим сравнение: 14 x º19(mod25). Решим его.
3, то сравнение имеет 3 класса решений. Сократив a, b и т на d =3, получим сравнение: 14 x º19(mod25). Решим его.
2) Составим дробь  =
=  и преобразуем её в цепную дробь:
и преобразуем её в цепную дробь:  =
= 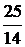 = [1; 1, 3, 1, 2]
= [1; 1, 3, 1, 2]
(проверьте!); п = 4.
3) Найдём Pn – 1 – числитель предпоследней подходящей дроби (для проверки вычис-
| лений найдём и Pn ):
| ak
| 1 1 3 1 2
| Pn – 1 = 9.
|
| Pk
| 1 2 7 9 25
|
4) Воспользуемся формулой (24) (при п = 4, b = 19, Pn – 1 = 9, т = 25):
х º (– 1) 4 ×19× 9 (mod25) Þ х º 171 º – 4 (mod25), или x = – 4 + 25 t, t Î Z.
5) При t =0,1, 2 получим 3 класса решений данного сравнения: х º – 4; 21; 46(mod75).
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Решите сравнения 1-й степени с одной неизвестной с помощью конечных цепных дробей:
312. 37 х º 73 (mod 91). 313. 54 х º 3 (mod 37). 314. 65 х º 111(mod 113).
315. 64 х º 5 (mod 235). 316. 55 х º 37 (mod 87). 317. 37 х º 32 (mod 54).
318. 76 х º 98 (mod 225). 319. 24 х º 34 (mod 62). 320. 34 х º 48 (mod 84).
321. 273 х º 42 (mod 369). 322. 84 х º 72 (mod 234). 323. 285 х º 177(mod 924).



 2, то сравнение имеет d = 2 классов решений по модулю 8 или 1 класс решений по модулю т: d = 8: 2, т.е. по модулю 4.
2, то сравнение имеет d = 2 классов решений по модулю 8 или 1 класс решений по модулю т: d = 8: 2, т.е. по модулю 4. Þ
Þ  Þ
Þ  (q Î Z) –бесконечное множество решений.
(q Î Z) –бесконечное множество решений.
 тi (i = 1, 2,..., s).
тi (i = 1, 2,..., s).
 (**)
(**)
 (***)
(***)
 (р 1 × р 2), то
(р 1 × р 2), то  Þ
Þ 
 2)
2)  ?
? 3, то система совместна.
3, то система совместна.
 Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ
 (Здесь т = [7; 9; 15] = 7 ×9 ×5 = 315).
(Здесь т = [7; 9; 15] = 7 ×9 ×5 = 315). Þ
Þ  Þ
Þ  Þ
Þ  Þ Þ
Þ Þ  Þ
Þ 
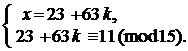 Þ
Þ  Þ
Þ  Þ
Þ Þ
Þ  Þ х = 23 + 63 (1 + 5 q) Þ x = 86 + 315 q.
Þ х = 23 + 63 (1 + 5 q) Þ x = 86 + 315 q. (Здесь т = [11; 35; 5] = 11×35 = 385).
(Здесь т = [11; 35; 5] = 11×35 = 385). Þ
Þ 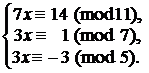 Þ
Þ  Þ
Þ 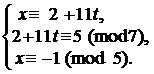 Þ
Þ Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ Þ
Þ  Þ х = – 9 + 77 (– 1 + 5 q) Þ х = – 86 + 385 q.
Þ х = – 9 + 77 (– 1 + 5 q) Þ х = – 86 + 385 q. Þ
Þ Þ
Þ  Þ
Þ  откуда х = 3 + 7(1 + 3 q) Þ
откуда х = 3 + 7(1 + 3 q) Þ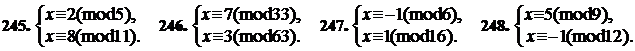
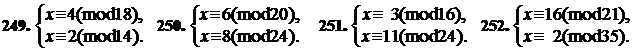
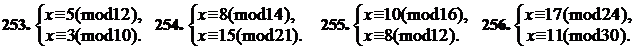
 258.
258.  259.
259.  260.
260. 






 ,
,

 = [4; 3, 1, 2], где n = 3.
= [4; 3, 1, 2], где n = 3.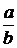 .
. .
.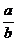 может быть представлено в виде конечной цепной дроби, причём единственным образом..
может быть представлено в виде конечной цепной дроби, причём единственным образом.. в конечную цепную дробь.
в конечную цепную дробь. =
=  преобразовать в конечную цепную дробь.
преобразовать в конечную цепную дробь. = [4; 3, 1, 2], где n = 3.
= [4; 3, 1, 2], где n = 3.
 = 4
= 4  ; А 2 = [4; 3, 1] = 4
; А 2 = [4; 3, 1] = 4  ; А 1 = [4;3] = 4
; А 1 = [4;3] = 4  ; А 0 = [4] = 4.
; А 0 = [4] = 4.

 – несократимая дробь. Если
– несократимая дробь. Если  , где Pk – числитель k-й подходящей дроби,
, где Pk – числитель k-й подходящей дроби,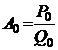 = [ a 0] Þ P 0 = а 0; Q 0 = 1.
= [ a 0] Þ P 0 = а 0; Q 0 = 1.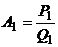 = [ a 0; a 1] Þ P 1 = а 1 × P 0 + 1; Q 1 = а 1.
= [ a 0; a 1] Þ P 1 = а 1 × P 0 + 1; Q 1 = а 1. = [ a 0; a 1, а 2] Þ P 2 = а 2 × P 1 + P 0; Q 2 = а 2 × Q 1 + Q 0.
= [ a 0; a 1, а 2] Þ P 2 = а 2 × P 1 + P 0; Q 2 = а 2 × Q 1 + Q 0. = [ a 0; a 1, а 2 , …, ak ] Þ Pk = аk × Pk – 1 + Pk – 2; Qk = аk × Qk – 1 + Qk – 2
= [ a 0; a 1, а 2 , …, ak ] Þ Pk = аk × Pk – 1 + Pk – 2; Qk = аk × Qk – 1 + Qk – 2
 .
. .
.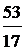 ; б)
; б)  ; в)
; в)  .
. = [3; 8, 2]; б)
= [3; 8, 2]; б)  = [2; 2, 1, 3]; в)
= [2; 2, 1, 3]; в)  = [5; 2, 1, 4, 12].
= [5; 2, 1, 4, 12]. ; А 1 =
; А 1 =  ; А 2 =
; А 2 =  ; А 3 =
; А 3 =  ;
б) А 0 =
;
б) А 0 =  ; А 1 =
; А 1 =  ; А 2 =
; А 2 =  ; А 3 =
; А 3 =  ; А 4 =
; А 4 =  .
.


 ;
б) А 3 =
;
б) А 3 =  .
.
 ; б)
; б)  .
.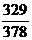 = [0; 1, 6, 1, 2, 2]
= [0; 1, 6, 1, 2, 2]
 = [2; 8, 1, 2]
= [2; 8, 1, 2]
 ;
б)
;
б)  .
.
 ; б) А 3 = [2; 2, 1, 5]; в) А 3 = [3; 11, 2, 4]; г) А 4 = [– 2; 1, 2, 1, 2].
; б) А 3 = [2; 2, 1, 5]; в) А 3 = [3; 11, 2, 4]; г) А 4 = [– 2; 1, 2, 1, 2].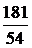 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =
=  ; б)
; б)  =
=  ; в)
; в)  ; г)
; г)  =
=  ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
. и преобразовать её в конечную цепную дробь:
и преобразовать её в конечную цепную дробь:  и преобразуем её в цепную дробь:
и преобразуем её в цепную дробь:  =[5; 2, 1, 4, 12]
=[5; 2, 1, 4, 12] =
=  и преобразуем её в цепную дробь:
и преобразуем её в цепную дробь: 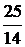 = [1; 1, 3, 1, 2]
= [1; 1, 3, 1, 2]

