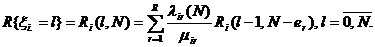Если поступления запросов являются нетипичными и стационарные вероятности их числа в момент поступления -
 запрос поступил сразу же после момента t },
запрос поступил сразу же после момента t },
необязательно равны соответствующим безусловным стационарным вероятностям
 ,
,
но для системы М/М/ 1:
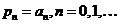 ,
,
тогда, для любого момента t и длины интервала  число запросов, поступивших в интервале
число запросов, поступивших в интервале  , не зависит от числа запросов, находящихся в системе в момент t. При использовании свойств пуассоновского процесса это эквивалентно предположению, что в любой момент времени длительность обслуживания поступивших ранее запросов и интервалы между будущими моментами поступлений являются независимыми, до некоторой степени это выполняется и в сетях пакетной передачи. Такое предположение справедливо, если процесс поступления является пуассоновским, а интервалы между моментами поступления и длительности обслуживания независимы.
, не зависит от числа запросов, находящихся в системе в момент t. При использовании свойств пуассоновского процесса это эквивалентно предположению, что в любой момент времени длительность обслуживания поступивших ранее запросов и интервалы между будущими моментами поступлений являются независимыми, до некоторой степени это выполняется и в сетях пакетной передачи. Такое предположение справедливо, если процесс поступления является пуассоновским, а интервалы между моментами поступления и длительности обслуживания независимы.
Равенство  , выполняется, так как, по предположению, события
, выполняется, так как, по предположению, события 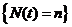 (запрос поступил сразу же после момента t) независимы. В результате условная вероятность будет равна безусловной.
(запрос поступил сразу же после момента t) независимы. В результате условная вероятность будет равна безусловной.
Пусть  соответствует событию, что запрос поступает в интервале
соответствует событию, что запрос поступает в интервале  и
и

 запрос поступает сразу же после момента t }.
запрос поступает сразу же после момента t }.
Используя формулы Байеса можно получить, что:


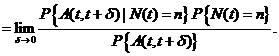
По предположению событие  не зависит от числа запросов, находящихся в системе в момент t. Следовательно
не зависит от числа запросов, находящихся в системе в момент t. Следовательно
 :
:  , а для
, а для  будет получена формула. Таким образом, если процесс поступления запросов пуассоновский, то поступивший в систему запрос определяется обычным состоянием.
будет получена формула. Таким образом, если процесс поступления запросов пуассоновский, то поступивший в систему запрос определяется обычным состоянием.
При распределении числа запросов в системе сразу же после того, как запрос покидает систему, вероятность равна:
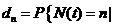 запрос поступает непосредственно перед моментом t }.
запрос поступает непосредственно перед моментом t }.
Соответствующие стационарные вероятности можно обозначить как  . При очень общих предположениях
. При очень общих предположениях  - система достигала стационарного состояния, в котором стационарные вероятности положительны при всех п, и число запросов N(t) имеет приращения, равные единице. Для любого увеличения состояния системы от п до п +1 из-за поступления нового запроса в дальнейшем будет соответствующее уменьшение от n +1 до п из-за ухода запроса из системы. Следовательно, при длительной работе доля переходов из п в п +1 среди общего их числа из любого k в k +1 равна доле переходов из п +1 в п среди всех переходов из любого k +1 в k,а
- система достигала стационарного состояния, в котором стационарные вероятности положительны при всех п, и число запросов N(t) имеет приращения, равные единице. Для любого увеличения состояния системы от п до п +1 из-за поступления нового запроса в дальнейшем будет соответствующее уменьшение от n +1 до п из-за ухода запроса из системы. Следовательно, при длительной работе доля переходов из п в п +1 среди общего их числа из любого k в k +1 равна доле переходов из п +1 в п среди всех переходов из любого k +1 в k,а  , и в стационарном состоянии для поступающего и уходящего запроса система выглядит как статистически одинаковая.
, и в стационарном состоянии для поступающего и уходящего запроса система выглядит как статистически одинаковая.
Система М/М/M с M обслуживающими приборами
Уравнения равновесия для стационарных вероятностей  при
при  можно записать следующим образом:
можно записать следующим образом:
 ,
,  .
.
Из этих уравнений следует, что:

где 
Можно вычислить  , используя формулу и условие
, используя формулу и условие  Тогда:
Тогда:
 , и окончательно
, и окончательно
 .
.
Вероятность того, что поступивший запрос обнаружит в системе, что все обслуживающие приборы заняты, и будет поставлен в очередь для ожидания, равна
 ,
,
следовательно,
PQ □ P { встать в очередь }=  ,
,
где PQ можно определить из формулы Эрланга.
Математическое ожидание числа запросов, находящихся в очереди равно: MO 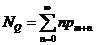 .
.
 дает условное математическое ожидание числа запросов, ожидающих в очереди при поступлении запроса, при условии, что этот запрос направляется в очередь для ожидания. Математическое ожидание при заданном
дает условное математическое ожидание числа запросов, ожидающих в очереди при поступлении запроса, при условии, что этот запрос направляется в очередь для ожидания. Математическое ожидание при заданном  не зависит от числа обслуживающих приборов. Оно указывает, в частности, на то, что, если имеются запросы, ожидающие в очереди, длина очереди в системе М/М/т ведет себя так же, как в системе М/М/m со скоростью обслуживания
не зависит от числа обслуживающих приборов. Оно указывает, в частности, на то, что, если имеются запросы, ожидающие в очереди, длина очереди в системе М/М/т ведет себя так же, как в системе М/М/m со скоростью обслуживания 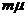 , равной суммарной скорости т обслуживающих приборов.
, равной суммарной скорости т обслуживающих приборов.
Следовательно, средняя задержка в системе равна
tз.ср =  + tож =
+ tож =  +
+ 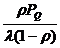 ,
,
и среднее число запросов в системе составляет

Система М/М/M/M с потерями и с Т обслуживающими приборами
Эта система подобна системе М/М/т за исключением того, что, если запрос при поступлении в систему обнаружит, что все т обслуживающих приборов заняты, он не поступит в систему, а потеряется, эта модель широко применяется в телефонии. В корпоративных компьютерных сетях такая модель может использоваться для исследования сети, в которой моменты поступления соответствуют заявкам на установление виртуальных соединений между двумя узлами, а максимально возможное число виртуальных связей равно т. Средняя длительность обслуживания  , в этом случае равна среднему времени использования виртуального соединения.
, в этом случае равна среднему времени использования виртуального соединения.
Пусть  так, что
так, что  Тогда, с учетом равенства
Тогда, с учетом равенства  получается:
получается:
 .
.
Система M/G/ 1
Можно проанализировать СМО с одной очередью, в которой запросы поступают в соответствии с пуассоновским процессом с интенсивностью  , но длительности обслуживания имеют произвольное распределение, не обязательно экспоненциальное, как в системе М/М/ 1. Запросы обслуживаются в порядке поступления, Txi - длительность обслуживания i -го запроса, случайные величины (Tx 1, Tx 2,…) одинаково распределены, взаимно независимы и не зависят от интервалов между моментами поступления.
, но длительности обслуживания имеют произвольное распределение, не обязательно экспоненциальное, как в системе М/М/ 1. Запросы обслуживаются в порядке поступления, Txi - длительность обслуживания i -го запроса, случайные величины (Tx 1, Tx 2,…) одинаково распределены, взаимно независимы и не зависят от интервалов между моментами поступления.
Пусть  - средняя длительность обслуживания,
- средняя длительность обслуживания,  - второй момент длительности обслуживания. Из формулы Поллячека — Хинчина:
- второй момент длительности обслуживания. Из формулы Поллячека — Хинчина:
 ,
,
где MOW - математическое ожидание времени пребывания запроса в очереди, а  .
.
Общее время пребывания в очереди и в обслуживающем приборе равно
 .
.
Применяя формулу Литтла для MOW и Т, можно получить математическое ожидание числа запросов в очереди MO 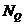 и математическое ожидание числа запросов в системе:
и математическое ожидание числа запросов в системе:
 .
.
Так как в случае M/D/ 1 при данном  получается минимально возможное значение
получается минимально возможное значение  , из этого следует, что при одинаковых значениях
, из этого следует, что при одинаковых значениях  и
и  величины MOW, T, MOQ и N для системы массового обслуживания M/D/ 1 являются нижними границами для соответствующих величин в системе M/G/ 1. Необходимо заметить, что MOW и MO
величины MOW, T, MOQ и N для системы массового обслуживания M/D/ 1 являются нижними границами для соответствующих величин в системе M/G/ 1. Необходимо заметить, что MOW и MO 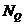 для системы M/D/ 1 равны половине их значений в системе М/М/ 1. Вместе с тем значения Т и N при малых
для системы M/D/ 1 равны половине их значений в системе М/М/ 1. Вместе с тем значения Т и N при малых  для M/D/ 1такие же, как в системе М/М/ 1, и приближаются к половине их значений в системе М/М/ 1 по мере того, как
для M/D/ 1такие же, как в системе М/М/ 1, и приближаются к половине их значений в системе М/М/ 1 по мере того, как  приближается к 1. Дело в том, что математическое ожидание длительности обслуживания одно и то же в обоих случаях и при малых
приближается к 1. Дело в том, что математическое ожидание длительности обслуживания одно и то же в обоих случаях и при малых  большую часть времени пребывания в системе запросы находятся в обслуживающем приборе, а при больших
большую часть времени пребывания в системе запросы находятся в обслуживающем приборе, а при больших  большую часть времени ожидают в очереди.
большую часть времени ожидают в очереди.
Системы M/G/ 1 с перерывами
Пусть T 1, T 2,… - продолжительности последовательных перерывов, которые делает обслуживающий прибор и T 1, T 2,… - независимые одинаково распределенные случайные величины, которые также не зависят от интервалов между моментами поступления запросов и длительностей их обслуживания. Моменты поступления образуют пуассоновский поток, а длительности обслуживания являются независимыми и имеют произвольное распределение. Вновь поступивший в систему запрос должен ждать в очереди завершения обслуживания текущего запроса или завершения перерыва, а затем должен ждать, пока будут обслужены все запросы, стоящие перед ним. Таким образом, выполняется равенство
MOW =  ,
,
где TR - среднее остаточное время для завершения обслуживания или перерыва в момент, когда поступает i -й запрос.
Если М(t) - число обслуживаний, которые завершились к моменту t, a L (t) - число перерывов, которые закончились к моменту t, то для любого момента t, когда точно завершается обслуживание или перерыв справедливо выражение:
 .
.
Предполагается, что среднее по времени можно заменить на среднее по вероятности и получить, что  при возрастании t, где
при возрастании t, где 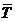 и
и 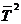 — первый и второй моменты длительности перерыва соответственно.
— первый и второй моменты длительности перерыва соответственно.
Тогда, учитывая, математическое ожидание времени, проведенного в очереди в системе M/G/ 1с перерывами равно:
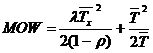 .
.
Пропускная способность узла
Пусть 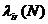 - интенсивность потока (i,r) -заданий, поступающих в узел i сети Q(M,N) в стационарном режиме. Очевидно, что
- интенсивность потока (i,r) -заданий, поступающих в узел i сети Q(M,N) в стационарном режиме. Очевидно, что  - относительная частота посещения r -заявкой узла
- относительная частота посещения r -заявкой узла 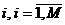 , приходящаяся на одно посещение некоторого выделенного УК i*. Интенсивность
, приходящаяся на одно посещение некоторого выделенного УК i*. Интенсивность 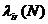 поступающего в узел i потока r- заявок равна интенсивности обслуженного этим узлом потока r- заявок.
поступающего в узел i потока r- заявок равна интенсивности обслуженного этим узлом потока r- заявок.
Следовательно 
При этом, маргинальное распределение общего числа заявок в узле удовлетворяет рекуррентному соотношению:
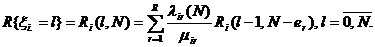





 запрос поступил сразу же после момента t },
запрос поступил сразу же после момента t }, ,
,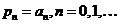 ,
, число запросов, поступивших в интервале
число запросов, поступивших в интервале  , не зависит от числа запросов, находящихся в системе в момент t. При использовании свойств пуассоновского процесса это эквивалентно предположению, что в любой момент времени длительность обслуживания поступивших ранее запросов и интервалы между будущими моментами поступлений являются независимыми, до некоторой степени это выполняется и в сетях пакетной передачи. Такое предположение справедливо, если процесс поступления является пуассоновским, а интервалы между моментами поступления и длительности обслуживания независимы.
, не зависит от числа запросов, находящихся в системе в момент t. При использовании свойств пуассоновского процесса это эквивалентно предположению, что в любой момент времени длительность обслуживания поступивших ранее запросов и интервалы между будущими моментами поступлений являются независимыми, до некоторой степени это выполняется и в сетях пакетной передачи. Такое предположение справедливо, если процесс поступления является пуассоновским, а интервалы между моментами поступления и длительности обслуживания независимы. , выполняется, так как, по предположению, события
, выполняется, так как, по предположению, события 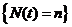 (запрос поступил сразу же после момента t) независимы. В результате условная вероятность будет равна безусловной.
(запрос поступил сразу же после момента t) независимы. В результате условная вероятность будет равна безусловной. соответствует событию, что запрос поступает в интервале
соответствует событию, что запрос поступает в интервале 
 запрос поступает сразу же после момента t }.
запрос поступает сразу же после момента t }.

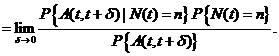
 :
:  , а для
, а для  будет получена формула. Таким образом, если процесс поступления запросов пуассоновский, то поступивший в систему запрос определяется обычным состоянием.
будет получена формула. Таким образом, если процесс поступления запросов пуассоновский, то поступивший в систему запрос определяется обычным состоянием.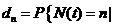 запрос поступает непосредственно перед моментом t }.
запрос поступает непосредственно перед моментом t }. . При очень общих предположениях
. При очень общих предположениях  - система достигала стационарного состояния, в котором стационарные вероятности положительны при всех п, и число запросов N(t) имеет приращения, равные единице. Для любого увеличения состояния системы от п до п +1 из-за поступления нового запроса в дальнейшем будет соответствующее уменьшение от n +1 до п из-за ухода запроса из системы. Следовательно, при длительной работе доля переходов из п в п +1 среди общего их числа из любого k в k +1 равна доле переходов из п +1 в п среди всех переходов из любого k +1 в k,а
- система достигала стационарного состояния, в котором стационарные вероятности положительны при всех п, и число запросов N(t) имеет приращения, равные единице. Для любого увеличения состояния системы от п до п +1 из-за поступления нового запроса в дальнейшем будет соответствующее уменьшение от n +1 до п из-за ухода запроса из системы. Следовательно, при длительной работе доля переходов из п в п +1 среди общего их числа из любого k в k +1 равна доле переходов из п +1 в п среди всех переходов из любого k +1 в k,а  , и в стационарном состоянии для поступающего и уходящего запроса система выглядит как статистически одинаковая.
, и в стационарном состоянии для поступающего и уходящего запроса система выглядит как статистически одинаковая. при
при  можно записать следующим образом:
можно записать следующим образом: ,
,  .
.

 , используя формулу и условие
, используя формулу и условие  Тогда:
Тогда: , и окончательно
, и окончательно .
. ,
, ,
,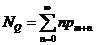 .
. дает условное математическое ожидание числа запросов, ожидающих в очереди при поступлении запроса, при условии, что этот запрос направляется в очередь для ожидания. Математическое ожидание при заданном
дает условное математическое ожидание числа запросов, ожидающих в очереди при поступлении запроса, при условии, что этот запрос направляется в очередь для ожидания. Математическое ожидание при заданном  не зависит от числа обслуживающих приборов. Оно указывает, в частности, на то, что, если имеются запросы, ожидающие в очереди, длина очереди в системе М/М/т ведет себя так же, как в системе М/М/m со скоростью обслуживания
не зависит от числа обслуживающих приборов. Оно указывает, в частности, на то, что, если имеются запросы, ожидающие в очереди, длина очереди в системе М/М/т ведет себя так же, как в системе М/М/m со скоростью обслуживания 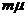 , равной суммарной скорости т обслуживающих приборов.
, равной суммарной скорости т обслуживающих приборов. + tож =
+ tож = 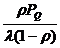 ,
,
 , в этом случае равна среднему времени использования виртуального соединения.
, в этом случае равна среднему времени использования виртуального соединения. так, что
так, что  Тогда, с учетом равенства
Тогда, с учетом равенства  получается:
получается: .
. , но длительности обслуживания имеют произвольное распределение, не обязательно экспоненциальное, как в системе М/М/ 1. Запросы обслуживаются в порядке поступления, Txi - длительность обслуживания i -го запроса, случайные величины (Tx 1, Tx 2,…) одинаково распределены, взаимно независимы и не зависят от интервалов между моментами поступления.
, но длительности обслуживания имеют произвольное распределение, не обязательно экспоненциальное, как в системе М/М/ 1. Запросы обслуживаются в порядке поступления, Txi - длительность обслуживания i -го запроса, случайные величины (Tx 1, Tx 2,…) одинаково распределены, взаимно независимы и не зависят от интервалов между моментами поступления. - средняя длительность обслуживания,
- средняя длительность обслуживания,  - второй момент длительности обслуживания. Из формулы Поллячека — Хинчина:
- второй момент длительности обслуживания. Из формулы Поллячека — Хинчина: ,
, .
. .
.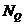 и математическое ожидание числа запросов в системе:
и математическое ожидание числа запросов в системе: .
. получается минимально возможное значение
получается минимально возможное значение  , из этого следует, что при одинаковых значениях
, из этого следует, что при одинаковых значениях  для M/D/ 1такие же, как в системе М/М/ 1, и приближаются к половине их значений в системе М/М/ 1 по мере того, как
для M/D/ 1такие же, как в системе М/М/ 1, и приближаются к половине их значений в системе М/М/ 1 по мере того, как  ,
, .
. при возрастании t, где
при возрастании t, где 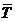 и
и 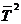 — первый и второй моменты длительности перерыва соответственно.
— первый и второй моменты длительности перерыва соответственно.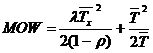 .
.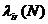 - интенсивность потока (i,r) -заданий, поступающих в узел i сети Q(M,N) в стационарном режиме. Очевидно, что
- интенсивность потока (i,r) -заданий, поступающих в узел i сети Q(M,N) в стационарном режиме. Очевидно, что  - относительная частота посещения r -заявкой узла
- относительная частота посещения r -заявкой узла 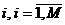 , приходящаяся на одно посещение некоторого выделенного УК i*. Интенсивность
, приходящаяся на одно посещение некоторого выделенного УК i*. Интенсивность