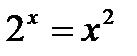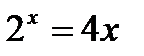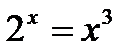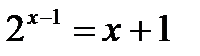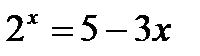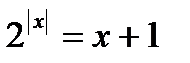Самостоятельная работа (4 часа)
Цель: изучить свойства графиков тригонометрических функций.
Графики и свойства тригонометрических функций.
При введении тригонометрических функций мы обозначали аргумент буквой t, т.к. буквы х и у были заняты – они обозначали координаты вращающейся точки М (t). Сейчас вернемся к прежним обозначениям: х – аргумент, у – функция.
Построим графики функций y = sin x, y = cos x, y = tg x и y = ctg x.
Для изображения графиков тригонометрических функций масштаб по осям выбирается 1 ед = 2 кл. Т.к. аргумент выражается чаще всего долями числа p, то разметим ось абсцисс используя приблизительное равенство p» 3. Тогда числу p соответствует 6 клеток, p/2 — 3 клетки, p/6 — 1 клетка и т.д. Получим т.н. тригонометрический набор координат.
Нанеся на координатную плоскость точки из таблицы значений тригонометрических функций (табл. 1) и соединив их плавной линией, получим искомые графики.
При построении тригонометрических функций мы используем радианную меру измерения углов.
Тогда функция y = sin x представляется графиком (рис.19). Эта кривая называется синусоидой.
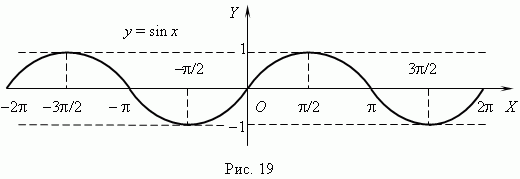
график - синусоида
Свойства функции
Область определения: R
Область значений: [-1; 1]
Четность, нечетность: функция нечетная
Период: 2π
Нули: sin x = 0 при x = π n, n  Z
Z
Промежутки знакопостоянства:
sin x > 0 при x  (2 π n; n + 2 π n), n
(2 π n; n + 2 π n), n  Z
Z
sin x < 0 при x  (- π + 2 π n; 2 π n), n
(- π + 2 π n; 2 π n), n  Z
Z
Экстремумы:
x min = π + 2 π n, n  Z; ymin = -1
Z; ymin = -1
x max = π + 2 π n, n  Z; ymin = 1
Z; ymin = 1
Промежутки монотонности:
Функция возрастает при x  [-
[- 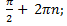
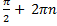 ], n
], n  Z
Z
Функция убывает при x  [
[ 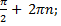
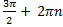 ], n
], n  Z
Z
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на  2
2
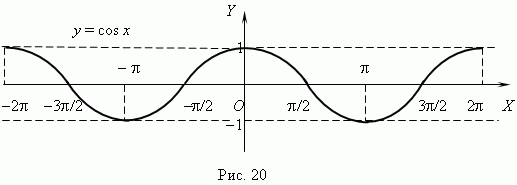
график - косинусоида
Свойства функции
Область определения: R
Область значений: [-1; 1]
Четность, нечетность: функция четная
Период: 2 π
Нули: 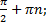 n
n  Z
Z
Промежутки знакопостоянства: cos x > 0 при x  (-
(- 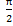 +2 π n;
+2 π n;  + 2 π n), n
+ 2 π n), n  Z
Z
cos x < 0 при x  (
( + 2 π n;
+ 2 π n; 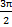 + 2 π n), n
+ 2 π n), n  Z
Z
Экстремумы:
x min = π + 2 π n, n  Z; ymin = -1
Z; ymin = -1
x max = 2 π n, n  Z; ymin = 1
Z; ymin = 1
Промежутки монотонности:
Функция возрастает при x  [-
[- 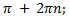
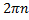 ], n
], n  Z
Z
Функция убывает при x  [
[ 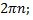
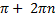 ], n
], n  Z
Z
Преобразования графиков y = sinx и y = cosx:
Графики функций y = sinx и y = cosx можно получить друг из друга путем параллельных переносов
вдоль оси x на  : cos x = sin (x +
: cos x = sin (x +  ); sin x = cos (x -
); sin x = cos (x -  );
);
Из этих графиков очевидны характеристики и свойства этих функций:
- область определения: 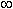 < x +
< x +  область значений: 1
область значений: 1 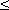 y
y 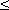 +1;
+1;
- эти функции периодические: их период 2  ;
;
- функции ограниченные (| y | 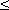 , всюду непрерывные, не монотонные, но
, всюду непрерывные, не монотонные, но
имеющие так называемые интервалы монотонности, внутри которых они
ведут себя, как монотонные функции (см. графики рис.19 и рис.20);
- функции имеют бесчисленное множество нулей.
y= tg x
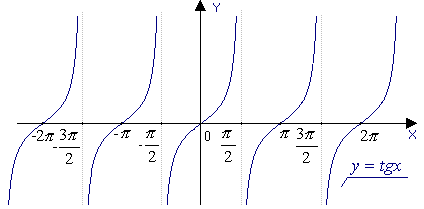
график - тангенсоида
Свойства функции
Область определения: объединение интервалов (- 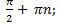
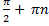 ), n
), n  Z
Z
Область значений: R
Четность, нечетность: функция нечетная
Период: 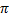
Нули: y = 0 при x = 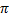 n, n
n, n  Z
Z
Промежутки знакопостоянства: tg x > 0 при x  (π n;
(π n;  + 2 π n), n
+ 2 π n), n  Z
Z
tg x < 0 при x  (-
(- 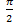 +2 π n; π n), n
+2 π n; π n), n  Z
Z
Экстремумов нет
Промежутки монотонности:
функция возрастает на каждом интервале области определения
Асимптоты: x = 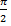 +
+ 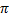 n, n
n, n  Z
Z
y = ctg x
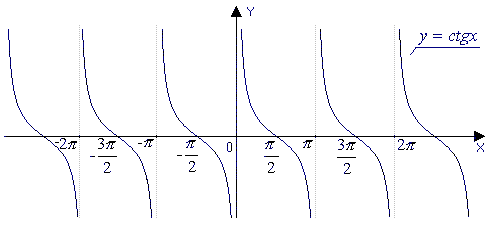
график - катангенсоида
Свойства функции
Область определения: объединение интервалов (π n; π+ π n), n  Z
Z
Область значений: R
Четность, нечетность: функция нечетная
Период: π
Нули: y = 0 при x =  +2 π n, n
+2 π n, n  Z
Z
Промежутки знакопостоянства: ctg x > 0 при x  (π n;
(π n;  + π n), n
+ π n), n  Z
Z
ctg x < 0 при x  (-
(-  + π n; π n), n
+ π n; π n), n  Z
Z
Экстремумов нет
Промежутки монотонности:
функция убывает на каждом интервале области определения
Асимптоты: x = π n, n  Z
Z
Преобразования графика y = ctgx:
График функци y = ctgx получается из графика y = tgx путем отражения относительно любой из координатныхосей и последующим параллельным переносом вдоль оси x на  .
.
Контрольные вопросы.
Тест для самопроверки.
18. Тригонометрические функции определены при любом х
19. Функция у = ctg x определена на (π n; π+ π n),.
20. Областью определения функции у =tg x является объединение интервалов (- 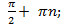
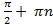 .)
.)
21. Областью значений каких тригонометрических функций является множество [-1; 1]
22. При построении тригонометрических функций мы используем ….меру измерения углов.
23. Функция y = sin x представляется графиком…….
24. Областью определения каких тригонометрических функций является R
25. Какие тригонометрические функции четные, нечетные.
26. Тригонометрические функции периодичны.
27. sin x > 0 при x 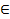 (2 π n; n + 2 π n), n
(2 π n; n + 2 π n), n 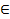 Z
Z
28. cos x < 0 при x 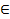 (
( + 2 π n;
+ 2 π n; 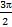 + 2 π n), n
+ 2 π n), n 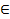 Z
Z
29. Нули функции y = cos x: 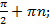 n
n 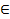 Z
Z
30. Экстремумы какой функции x min = π + 2 π n, n 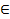 Z; ymin = -1 x max = 2 π n, n
Z; ymin = -1 x max = 2 π n, n 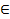 Z; ymin = 1?
Z; ymin = 1?
31. Как можно получить друг из друга графики функций y = sinx и y = cosx?
32. Логарифмическая функция имеет экстремум в точке (1; 0).
33. График функции у= cos x пересекается с осью ОХ в точках….
34. График логарифмической функции находится в верхней полуплоскости.
35. График логарифмической функции симметричен относительно ОХ.
36. График логарифмической функции пересекает ОХ в точке (1; 0).
37. График логарифмической функции находится в 1 и 4 четвертях.
38. Существует логарифм отрицательного числа.
39. Существует логарифм дробного положительного числа.
40. График логарифмической функции проходит через точку (0; 0).
Самостоятельная работа №15(2 часа)
Цель: изучить преобразования графиков функций.
изучить симметрию графиков относительно прямой Y=X.
| Способы построения графиков функций
|
| «по точкам»
|
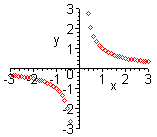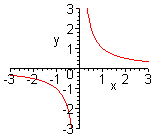
| Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями. (На графике функция 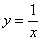 ). ).
|
| Путем сдвига графиков основных функций
|
| Чтобы построить график функции 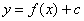 , можно или график функции , можно или график функции 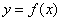 сдвинуть вдоль оси сдвинуть вдоль оси 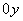 на на 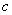 единиц в сторону, совпадающую со знаком единиц в сторону, совпадающую со знаком 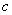 , или перенести параллельно ось , или перенести параллельно ось 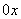 в сторону, противоположную знаку в сторону, противоположную знаку 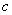 . (На примере функции . (На примере функции 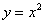 и и 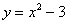 ). ).
|
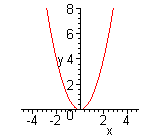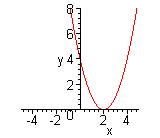
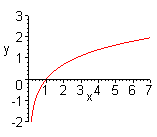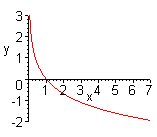
| Чтобы построить график функции 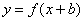 , можно или график функции , можно или график функции 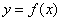 вдоль оси вдоль оси 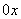 на на 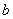 единиц в сторону, противоположную знаку единиц в сторону, противоположную знаку 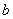 , или перенести параллельно ось , или перенести параллельно ось 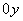 в сторону, совпадающую со знаком в сторону, совпадающую со знаком 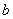 . (На примере функции . (На примере функции 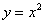 и и 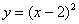 ). ).
|
| путем симметричного отображения относительно осей координат
|
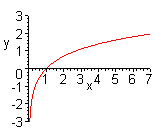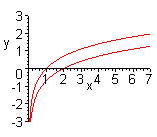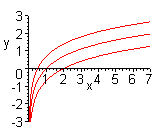
| Чтобы построить график функции 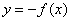 , можно построить изображение, симметричное графику функции , можно построить изображение, симметричное графику функции 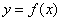 относительно оси относительно оси 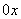 . (На примере функции . (На примере функции 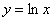 и и 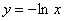 ). ).
|
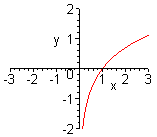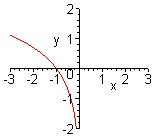
| Чтобы построить график функции 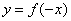 , можно построить изображение, симметричное графику функции , можно построить изображение, симметричное графику функции 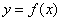 относительно оси относительно оси 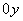 . (На примере функции . (На примере функции 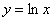 и и 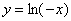 ). ).
|
| Путем деформирования графиков основных функций
|
| Чтобы построить график функции 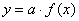 при при 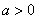 , можно график функции , можно график функции 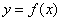 растянуть (сжать) вдоль оси растянуть (сжать) вдоль оси 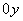 , если , если 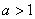 ( ( 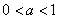 ). (На примере функции ). (На примере функции 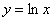 , , 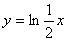 и и 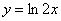 ). ).
|
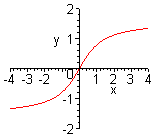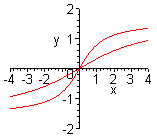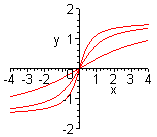
| Чтобы построить график функции 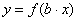 при при 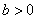 , можно график функции , можно график функции 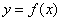 растянуть (сжать) вдоль оси растянуть (сжать) вдоль оси 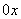 , если , если 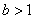 ( ( 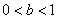 ). ). 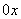 . . 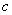 .(На примере функции .(На примере функции 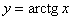 , , 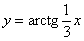 и и 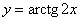 ). ).
|
| Способы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины
|
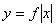
|
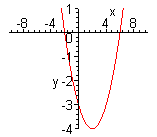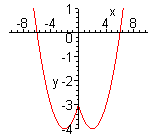
| Функция 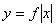 четная. Чтобы построить ее график, достаточно построить для четная. Чтобы построить ее график, достаточно построить для 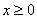 график функции график функции 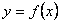 , а затем достроить его левую часть, симметричную правой относительно оси , а затем достроить его левую часть, симметричную правой относительно оси 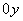 . (На примере функции . (На примере функции 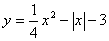 ). ).
|
|
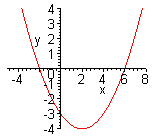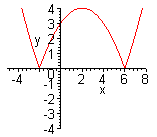
| Можно данную функцию рассматривать как совокупность двух функций: 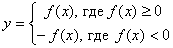 . Чтобы построить график функции . Чтобы построить график функции 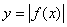 , достаточно построить график функции , достаточно построить график функции 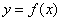 и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси  . (На примере функции . (На примере функции 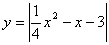 ) )
|
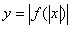
|
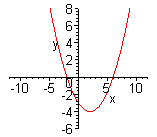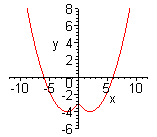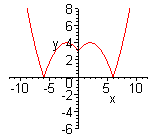
| Функция 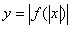 четная. Построить для четная. Построить для 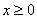 график функции график функции 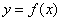 , затем его симметрично отразить относительно оси , затем его симметрично отразить относительно оси 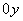 , и, наконец, ту часть полученного графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси , и, наконец, ту часть полученного графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси 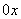 . (На примере функции . (На примере функции 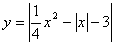 ). ).
|
| Кусочно-линейная функция
|
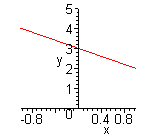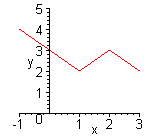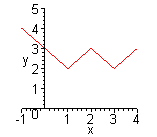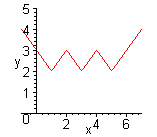
| Графиком кусочно-линейной функции является ломаная линия. Для построения графика находят уравнения звеньев ломаной.(Функция 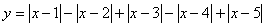 ). Уравнения звеньев ломаной: ). Уравнения звеньев ломаной: 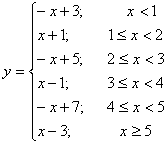
|
Преобразования графиков с помощью параллельного переноса
|
|
|
| Вариант 1
| Номер задания
|
|
|
|
|
|
|
|
|
| Вариант ответа
|
|
|
|
|
|
|
|
|
|
| Укажите для каждой функции ее график
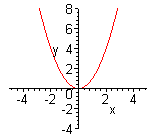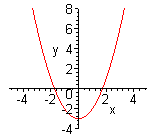
1. у = –х2 + 3 3. у = (х – 3)2 5. у = (х – 4)2 – 2
2. у = –х2 + 4 4. у = –(х + 3)2 6. у = (х + 4)2 – 2
|
|
|
|
|
Найти область определения функции.
1. 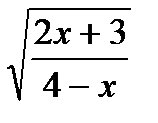 ;
;
2. 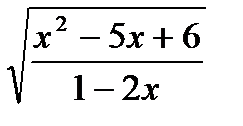
3. 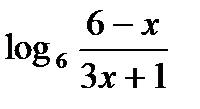 ;
;
4. 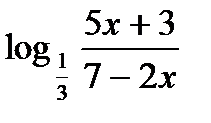
№5.19 (построить графики)
1) 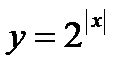 ;
;
2) 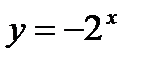 ;
;
3) 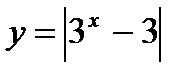 ;
;
4) 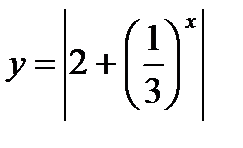 ;
;
5) 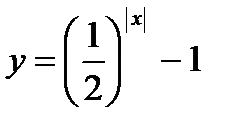 ;
;
6) 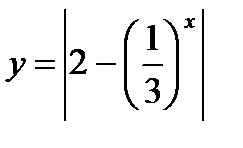 ;
;
7) 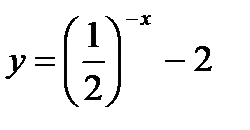 .
.
№ 5.20 (Решить уравнения графически):
1) 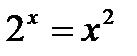
2) 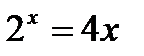
3) 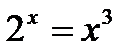
4) 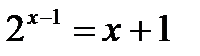
5) 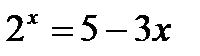
6) 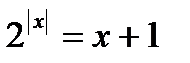
Контрольные вопросы.
Какие преобразования вы знаете?
Какие преобразования позволяют сдвигать график функции вдоль осей?
Какие преобразования позволяют сжимать график функции вдоль осей?
Какие преобразования позволяют симметрично отображать график функции относительно осей?



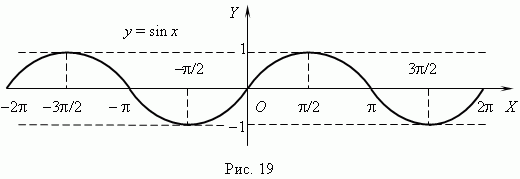
 Z
Z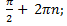
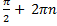 ], n
], n 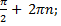
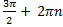 ], n
], n  2
2
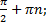 n
n 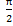 +2 π n;
+2 π n;  + 2 π n), n
+ 2 π n), n 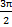 + 2 π n), n
+ 2 π n), n 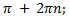
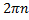 ], n
], n 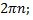
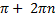 ], n
], n  : cos x = sin (x +
: cos x = sin (x +  < x +
< x +  y
y 
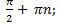
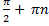 ), n
), n 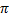
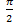 +2 π n; π n), n
+2 π n; π n), n 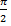 +
+ 
 .
.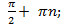
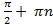 .)
.)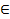 (2 π n; n + 2 π n), n
(2 π n; n + 2 π n), n  + 2 π n;
+ 2 π n; 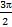 + 2 π n), n
+ 2 π n), n 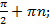 n
n 
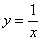 ).
).

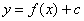 , можно или график функции
, можно или график функции 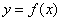 сдвинуть вдоль оси
сдвинуть вдоль оси 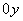 на
на 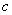 единиц в сторону, совпадающую со знаком
единиц в сторону, совпадающую со знаком 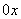 в сторону, противоположную знаку
в сторону, противоположную знаку 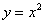 и
и 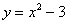 ).
).

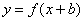 , можно или график функции
, можно или график функции 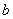 единиц в сторону, противоположную знаку
единиц в сторону, противоположную знаку 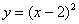 ).
).

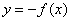 , можно построить изображение, симметричное графику функции
, можно построить изображение, симметричное графику функции 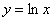 и
и 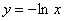 ).
).

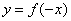 , можно построить изображение, симметричное графику функции
, можно построить изображение, симметричное графику функции 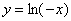 ).
).

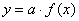 при
при 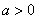 , можно график функции
, можно график функции 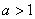 (
( 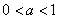 ). (На примере функции
). (На примере функции 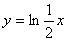 и
и 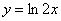 ).
).

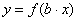 при
при 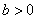 , можно график функции
, можно график функции 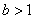 (
( 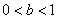 ).
). 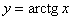 ,
, 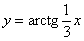 и
и 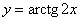 ).
).
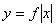

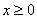 график функции
график функции 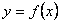 , а затем достроить его левую часть, симметричную правой относительно оси
, а затем достроить его левую часть, симметричную правой относительно оси 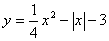 ).
).
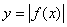

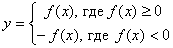 . Чтобы построить график функции
. Чтобы построить график функции 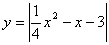 )
)
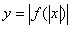

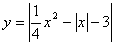 ).
).
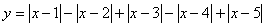 ). Уравнения звеньев ломаной:
). Уравнения звеньев ломаной: 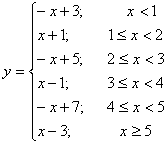
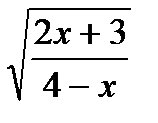 ;
;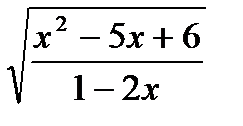
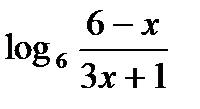 ;
;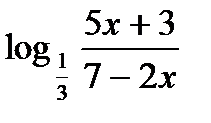
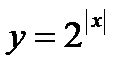 ;
;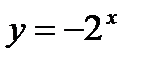 ;
;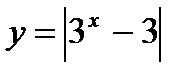 ;
;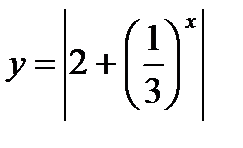 ;
;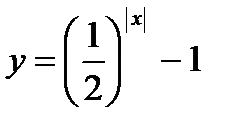 ;
;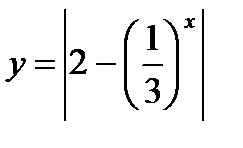 ;
;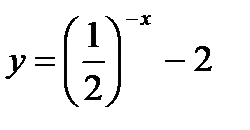 .
.