Этот метод имеет ограниченную область применения. Этим методом можно решать следующие задачи:
- Задачи с двумя переменными, имеющими симметричную форму записи.
- Задачи с n переменными, имеющие каноническую форму записи, если выполняется условие n-r≤2, где n – число неизвестных, r – ранг системы линейных уравнений (1).
Задача типа 2 сводится к задаче типа 1, для чего нужно перейти от канонической к симметричной форме записи.
Рассмотрим решение задач типа 1.
Найти X =(x1,x2), который является решением (1), удовл. (2),
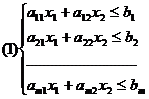
(2) x1≥0, x2≥0
и на котором целевая функция f(X)=c1x1+c2x2 (3) достигает экстремума (максимума или минимума).
Решение задачи содержит два этапа:
I. Построим ОДР


ОДР находится в 1-й координатной четверти
система (1) содержит линейные неравенства с двумя переменными
(7) 
Решением такого неравенства является любая пара чисел (x1; x2), которая при подстановке в (7) обращает его в верное числовое равенство.
На координатной плоскости (x1; x2) – точка.
Множество решений (7) – некоторое множество точек на x1Ox2.
Выясним, какую область на плоскости x1Ox2 образуют точки, которые являются решением ограничений (1) и (2).
Заменим неравенство (7) соответствующим ему равенством.
 - (8)
- (8)
это уравнение определяет на плоскости x1Ox2 прямую линию. Эта линия делит плоскость x1Ox2 на 2 полуплоскости π1 и π2.
Утверждение. Точки одной из этих полуплоскостей являются решением
 , (*)
, (*)
а точки другой полуплоскости являются решением неравенства  . (**)
. (**)
Докажем это утверждение.
Доказательство:
Возьмём т. M1 (x1’, x2’), М1  m
m
М0 – проекция т. М1
 ={x1’- x10; x2’- x20}
={x1’- x10; x2’- x20}
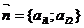
М0  m;
m; 
Выясним знак выражения  в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
т. 
 (*)
(*)
Знак выражения зависит от знака 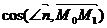
1) 

2) 
Тогда 


Для того, чтобы определить полуплоскость, в которой выполняются соответствующие неравенства, достаточно подставить в неравенство координаты какой-либо одной точки, не лежащей на граничной прямой.
Если неравенство удовлетворяется, то областью решения будет полуплоскость, в которой находится эта точка; если нет – то в другой.
Чтобы построить ОДР на координатной плоскости x10x2, нужно построить граничные прямые и области решений каждого неравенства системы; пересечение областей решения этих неравенств, взятое в первом квадранте и будет областью решений данной задачи.
II. Нахождение ОДР оптимального решения задачи.
Рассмотрим уравнение  (3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент
(3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент  ). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.

 - это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим
- это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим 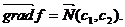
Определение.
Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, на которые данная линия уровня делит координатную плоскость, называется опорной прямой.
Чтобы найти ОДР оптимального решения, выполним:
1. Строим  в начале координат.
в начале координат.
2. Перпендикулярно  проводим одну из линий уровня, имеющую общие точки с ОДР.
проводим одну из линий уровня, имеющую общие точки с ОДР.
3. Перемещая эту линию уровня в направлении  в задаче на max или в противоположном направлении в задаче на min, находим опорную прямую.
в задаче на max или в противоположном направлении в задаче на min, находим опорную прямую.
4. Совместно решив уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой, найдем оптимальное решение. В зависимости от вида ОДР и целевой функции задача может иметь единственное решение, бесконечное множество решений, или не иметь решений ввиду несовместности системы ограничений или неограниченности целевой функции ОДР.
Пример.

Решим совместно уравнения прямых BC и DC, и имеющих общую точку с опорной прямой, найдём оптимальное решение.
§5. Преобразование однократного замещения.
Пусть дана система линейных уравнений
(1) 
r<n (ранг системы)
Приведём эту систему к разрешённому виду методом Жордано-Гаусса и выпишем общее решение системы (общее решение системы – это формулы, выражающие базисные неизвестные через свободные).
Общее решение
(1’) 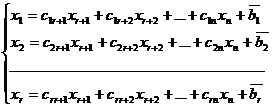
Положив в этих формулах значение всех свободных неизвестных, равных нулю, мы найдём базисное решение системы.

Исходная система (1) будет иметь не одно базисное решение, т.к. из n неизвестных можно составить разные наборы из r неизвестных, но не каждый такой набор из r неизвестных можно взять за базисные неизвестные, т.к. среди r векторов коэффициентов при этих неизвестных могут быть линейно зависимые и, следовательно, базиса из них составить нельзя. Если мы знаем какое-либо одно базисное решение, то, преобразовав систему от одного единичного базиса к другому, можем найти любое другое базисное решение системы.
Пример.
Дана система линейных уравнений, приведённая к единичному базису. Требуется преобразовать её к какому-либо другому единичному базису.





| Базисные неизвестные
| x1
| x2
| x3
| x4
| x5
| bi
| Базисное решение
|
| x1,x4,x5
|
|
-3
| 

|
|
| 
| 
|
|
|

|
-3

| 
|
|
| 
|
|
| x3,x4,x5
| 
| 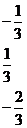
|
|
|
| 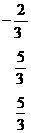
| 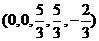
|
Для того чтобы найти какой-либо другой единичный базис, возьмём за разрешающий элемент любой неравный нулю коэффициент при каком-либо свободном неизвестном и выполним одну итерацию методом Жордано-Гаусса.
Свободное неизвестное x3 стало базисным, а базисное неизвестно x1 стало свободным. Такое преобразование называется преобразованием однократного замещения, т.к. произошло замещение базисного неизвестного x1 свободным неизвестным x3. Т.о. данная система уравнений преобразована к новому единичному базису, в котором вектор-коэффициенты при x3,x4,x5. Последовательно выполняя преобразования однократного замещения, можно найти все базисы векторов коэффициентов и все базисы решений данной системы.
Замечание.
Для данной системы уравнений нельзя в качестве базисных неизвестных взять набор x1,x2,x4, т.к. им соответствуют вектор-коэффициенты 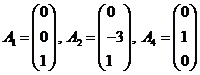 , которые линейно зависимы, т.к. А1-А2-3А4=θ.
, которые линейно зависимы, т.к. А1-А2-3А4=θ.



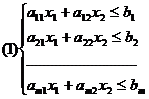



 - (8)
- (8) , (*)
, (*) . (**)
. (**) m
m ={x1’- x10; x2’- x20}
={x1’- x10; x2’- x20}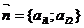
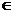 m;
m; 
 в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
 (*)
(*)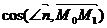






 (3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент
(3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент  ). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
 - это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим
- это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим 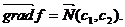
 в начале координат.
в начале координат. проводим одну из линий уровня, имеющую общие точки с ОДР.
проводим одну из линий уровня, имеющую общие точки с ОДР.

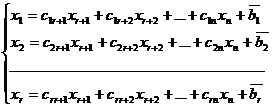










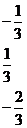
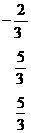
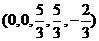
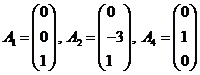 , которые линейно зависимы, т.к. А1-А2-3А4=θ.
, которые линейно зависимы, т.к. А1-А2-3А4=θ.


