

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
Топ:
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Рассмотрим свободные колебания системы с конечным числом степеней свободы. В качестве объекта рассмотрим упругую невесомую балку, изображенную на рис.14.3 и с n сосредоточенными массами m 1, m 2, m 3,..., mn. Пренебрегаем продольными деформациями оси балки в процессе колебаний. При этом положение системы однозначно определяется перемещениями сосредоточенных масс yi (t) (i = 1,2,3,..., n) в произвольные моменты времени t, вызванными упругими деформациями балки в поперечном направлении.

Рис.14.3
Во время движения, пренебрегая сопротивлением внутренних и внешних сил, на балку будут действовать в качестве внешних сил инерционные силы  , (i = 1,2,3,..., n). Применяя метод сил, перемещение произвольной массы yi (t) записывается в виде суммы:
, (i = 1,2,3,..., n). Применяя метод сил, перемещение произвольной массы yi (t) записывается в виде суммы:
 , (14.11)
, (14.11)
где  - перемещение i- ой массы от статической единичной силы, приложенной к k- ой массе от статической единичной силы по направлению соответствующей инерционной силы.
- перемещение i- ой массы от статической единичной силы, приложенной к k- ой массе от статической единичной силы по направлению соответствующей инерционной силы.
Подставляя выражение инерционных сил в систему уравнений (14.11), получим:
 , (i = 1,2,3,...,n). (14.12)
, (i = 1,2,3,...,n). (14.12)
Система дифференциальных уравнений движения (14.12), описывающая свободные колебания заданной балки, представляет собой замкнутую систему дифференциальных уравнений второго порядка с постоянными коэффициентами, решение которой в общем случае записывается в виде:
 . (14.13)
. (14.13)
Рассмотрим одно частное произвольное решение соответствующее r- ой форме колебаний:
 . (14.14)
. (14.14)
Подставляя (14.14) в (14.12) получим:
 , (14.15)
, (14.15)
которое распадается на две группы уравнений:
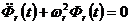 (14.16)
(14.16)
и
 (14.17)
(14.17)
Решение уравнения (14.16) записывается в виде:
 , (r = 1,2,3,..., n). (14.18)
, (r = 1,2,3,..., n). (14.18)
Как видно из (14.18), по произвольной форме r = 1,2,3,..., n колебания происходят по гармоническому закону с частотой  . Здесь
. Здесь  - частота собственных колебаний заданной системы, соответствующая r- ой форме.
- частота собственных колебаний заданной системы, соответствующая r- ой форме.
|
|
Согласно (14.14)  - является перемещением i- ой массы при r- ой форме колебания, значения которой определяется из решения системы алгебраических уравнений (14.17).
- является перемещением i- ой массы при r- ой форме колебания, значения которой определяется из решения системы алгебраических уравнений (14.17).
Система (14.17) относительно  (i = 1,2,3,..., n) имеет различные решения. Очевидно, решение
(i = 1,2,3,..., n) имеет различные решения. Очевидно, решение  º 0 свидетельствует об отсутствии движения системы, т.е. состояние покоя системы, которое нас не интересует.
º 0 свидетельствует об отсутствии движения системы, т.е. состояние покоя системы, которое нас не интересует.
Система (14.17) может иметь решения, отличные от нулевого лишь в том случае, когда ее определитель равен нулю, т.е. когда выполняется условие:
 , (14.19)
, (14.19)
где принято обозначение  .
.
Раскрывая определитель (14.19), получаем уравнения n -ой степени относительно  , а при его решении получим n значений
, а при его решении получим n значений  . Каждому значению
. Каждому значению  (r = 1,2,3,..., n) будет соответствовать своя собственная частота:
(r = 1,2,3,..., n) будет соответствовать своя собственная частота:
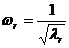 ,
,
и свой собственный вектор:
 .
.
При этом собственные формы упругих систем ортогональны между собой:
 , (r, k = 1,2,3,..., n; r ¹ k). (14.20)
, (r, k = 1,2,3,..., n; r ¹ k). (14.20)
Величины  непосредственно из решения (14.17) определить нельзя, они могут быть найдены с точностью до произвольного постоянного множителя, т.е. по существу могут быть найдены отношения между
непосредственно из решения (14.17) определить нельзя, они могут быть найдены с точностью до произвольного постоянного множителя, т.е. по существу могут быть найдены отношения между  . Принимая обозначения
. Принимая обозначения  система (14.17) преобразуется в вид:
система (14.17) преобразуется в вид:

Последняя система имеет одно лишнее уравнение, так как имеем n уравнений относительно (n -1) неизвестных  . Отбрасывая одно из этих уравнений, решая оставшуюся систему определяют все неизвестные
. Отбрасывая одно из этих уравнений, решая оставшуюся систему определяют все неизвестные  .
.
Далее, полагая  , по формуле
, по формуле  определяются все остальные амплитуды перемещений масс при r- ой произвольной форме колебаний.
определяются все остальные амплитуды перемещений масс при r- ой произвольной форме колебаний.
Возвращаясь к выражению (14.13) с учетом (14.18) можем записать:
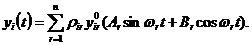 (14.21)
(14.21)
Учитывая, что  , Ar и Br являются произвольными постоянными, решение (14.21) можно записать в более удобной форме:
, Ar и Br являются произвольными постоянными, решение (14.21) можно записать в более удобной форме:
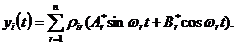
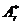 и
и  можно выразить через начальные условия каждой массы при t = 0, которыми являются перемещения i -ой массы
можно выразить через начальные условия каждой массы при t = 0, которыми являются перемещения i -ой массы  и ее скорости
и ее скорости  , и следовательно, задача о свободных колебаниях системы с произвольным числом свободы будет полностью решена.
, и следовательно, задача о свободных колебаниях системы с произвольным числом свободы будет полностью решена.
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!