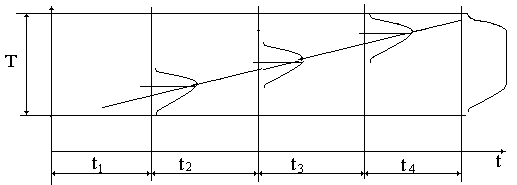
Наблюдения за изготовлением деталей на станке с одной настройки при неизменных условиях и измерением одним и тем же инструментом или прибором выявляют наличие рассеяния размеров, что указывает на наличие случайной составляющей погрешности на закономерно изменяющемся или постоянном уровне. Сам уровень характеризует систематическую составляющую погрешности.
Систематической погрешностью называется составляющая погрешности, которая остаётся постоянной или изменяется по определённому закону в зависимости от случайных факторов.
Систематической погрешность может быть постоянной и переменной. Например, неточность настройки прибора, отклонение от рабочей температуры – это постоянные систематические погрешности. При этом математическое ожидание: МХ = а. При переменных систематических погрешностях (например, износ инструмента) математическое ожидание будет: МХ (t)= a(t).
Cистематические погрешностиможно частично или полностью устранить, используя поправочные коэффициенты. Если полностью устранить не удаётся, то
их учитывают в допуске на размер.
Случайной составляющей погрешностью называется погрешность, которая изменяется случайно в зависимости от множества факторов не постоянных по величине и по знаку. Например, повторные измерения.
Эти погрешности определить и устранить невозможно, их можно только уменьшить. Например, стабилизировать усилие зажима.
При помощи теории вероятности и математической статистики можно оценить только суммарное значение случайных погрешностей измерения.
Случайные погрешности измерения могут быть дискретными (например, разброс диаметров поверхностей) или непрерывными (например, изменение диаметров измеренных вдоль оси цилиндра).
При проведении большого числа повторных измерений появление случайных погрешностей измерения подчиняется определённым закономерностям, изучением которых занимается теория вероятностей и математическая статистика. С точки зрения последней случайную погрешность измерения можно охарактеризовать с помощью распределения вероятности их появления или плотностью распределения вероятности Рх (хi), представляющую собой предел отношения вероятности того, что случайная величина х находится в пределах от Х до Х +D Х и величине интервала Dх.
Рх (хi) = lim [ Р(х < Х < х+Dх)] / Dх
Обычно характер рассеяния размеров подчиняется определённому закону распределения.
1. Закон Максвелла. Ему подчиняется рассеяние торцевого и радиального биения

2. Экспоненциальный закон Вейбула – Гнеденко. Ему подчиняются рассеяния отказов машин:

3. Закон нормального распределения (закон Гауса). Этому закону подчиняются суммарные погрешности, когда ни один из факторов не является превалирующим. Например, погрешности измерения размеров.


у – плотность вероятности погрешностей измерений, е = 2,718;
Вид кривой и её положение по оси Х полностью определяется математическим ожиданием. Математическое ожидание МХ характеризуеттеоретическое значение среднеарифметической погрешности DХ при бесконечно большом количестве измерений:
для дискретной величины - МХ = а = åхiр(х i),
для непрерывной - МХ = ò х px (x) dx
Значение МХ характеризует положение центра группирования случайных величин.
Параметр б– среднеквадратичное отклонение как мера рассеяния результатов измеренийопределяется:
для дискретной - б =Öå(хI- МХ )2 р(х i);
для непрерывной - б =Öò (хI- МХ )2 px (x) dx.
Случайные погрешности влияют на форму кривой распределения, т.е. при его уменьшении происходит сужение кривой, при увеличении - расширение.

Систематическая погрешность на форму кривой не влияет, но смещает центр группирования, при этом амплитуда кривой не изменяется:
- для постоянной, например, на величину погрешности настройки прибора:

- для переменной, например, износ измерительного наконечника во времени:
На практике случайную величину погрешности измерения удобно выразить через нормированное отклонение:
T = DX / б, (DX"0, б"1).
Так как на практике мы оперируем конечным числом значений, то вместо б
Определяют среднеквадратичную погрешность (дисперсию) S"б:

Среднеквадратичная погрешность среднеарифметической величиныХсрравна 
Наиболее вероятным значением действительной величины является среднеарифметическое ее значение Хср = ΣХi/n.
Поэтому для снижения погрешности измерения используется измерение одной и той же величины не менее трёх раз, а затем определяют среднеарифметическую погрешность:

В математической статистике доказано, что отклонение среднеарифметического в Ön раз меньше, чем отклонение отдельных измерений. Погрешность результата измерений определяется 
Это не значит, что с увеличением количества измерений можно достичь бесконечной точности. Если эта величина меньше, чем разрешающая способность прибора, то дальнейшее увеличение количества измерений бессмысленна.При числе измерений n< 30 используется коэффициент
Стъюдента:

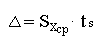 Увеличивать число измерений следует до тех пор, пока доверительный интервал, который определяется по формуле:
Увеличивать число измерений следует до тех пор, пока доверительный интервал, который определяется по формуле:
будет меньше возможной точности измерения инструментом или прибором, равной: Сси = цд /2, а для ответственных измерений: Сси = цд /3, гдецд-цена деления.Доверительные границы результатов измерений являются предельные значения случайных величин Х. Найти границы доверительного интервала, дисперсии при нормальном распределении и известной доверительной вероятности можно с помощью распределения Пирсона.
Функция для треугольного закона Симпсона выражается соотношением:
(1/ά2) (ά - │∆│) при │∆│ ≤ ά, 0 при │∆│> ά
Функция для равномерного закона распределения выражается соотношением:
1/(2ά) при │∆│ ≤ ά, 0 при │∆│ > ά
Если неизвестна дисперсия, то используется распределение Стъюдента, а при известной дисперсии и неизвестном законе распределения используется неравенство Чебышева.
Качество измерений характеризуется сходимостью результатов измерений, а их повторяемость воспроизводимостью.
Качество измерений определяется относительной погрешностью δ, т.к.
δ = Δ · 100% / Хи, т.е. с уменьшением Хи δ увеличивается.
Хи - измеряемая величина.
Приведенная погрешность, определяемая по формуле γ = Δ· 100% / Хн, численно равна классу точности прибора.
Хн – диапазон измерения прибора.
В основе определения предела допустимой погрешности измерения лежит принцип – реальная погрешность измерения всегда имеет предел.
Погрешность измерения называется мультипликативной, если она изменяется пропорционально изменению измеряемой величины.
По форме количественного выражения погрешности измерения делятся на абсолютные и относительные.
В метрологии при оценке годности параметра возможны ошибки 1(первого) и 11(второго) рода, которые оцениваются уровнем значимостиq = 1- Р,
где Р - доверительная вероятность.
Ошибки 1 рода – когда q не должен быть достаточно малым, чтобы забраковать деталь при правильной оценке;
Ошибки 11 рода – слишком малое значение qможет привести к ложной оценке.
Поэтому уровень значимости должен находиться в пределах 0,02 ≤ q ≤ 0,1.
При планировании измерений во время экспериментов обязательно необходимо обратить внимание на характеристику объекта измерения.

















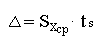 Увеличивать число измерений следует до тех пор, пока доверительный интервал, который определяется по формуле:
Увеличивать число измерений следует до тех пор, пока доверительный интервал, который определяется по формуле:


