Определение: Пусть  . Суммой чисел
. Суммой чисел 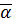 и
и  называется действительное число
называется действительное число 
Теорема: Множество  является аддитивной абелевой упорядоченной архимедовой группой. Сложение на
является аддитивной абелевой упорядоченной архимедовой группой. Сложение на  согласуется со сложением на
согласуется со сложением на 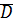 .
.
Доказательство:
· Сложение -б.а.о.По определению  .
.
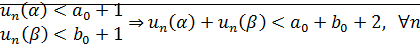
Поэтому множество 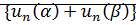 ограничено сверху и поэтому
ограничено сверху и поэтому 
· коммутативность
 – рациональные числа(конечные десятичные дроби), а сложение рац. чисел коммутативно.
– рациональные числа(конечные десятичные дроби), а сложение рац. чисел коммутативно.
· сложение на  и
и  согласуется.Обозначим сложение на
согласуется.Обозначим сложение на  как
как  , на
, на  как +.
как +.
1. 
2. 
3. 


Доказательство ОП.


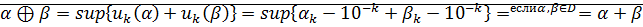
· ассоциативность. 


аналогично доказывается 
Согласно следствию теоремы о плотности 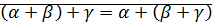
· существование нуля. 0 является нейтральным элементом относительно сложения.

· противоположный элемент. Каждый элемент имеет противоположный

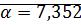


·  упорядоченная группа.
упорядоченная группа. 
· Архимедовость 

По свойству архимедовости для рациональных чисел

 ⊠
⊠
Определение: Упорядоченная аддитивная абелева группа, для которой выполняется свойство Архимеда, называется архимедовой.
Поле действительных чисел.
Определение:Модулем действительного числа 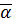 называется
называется
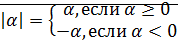
Определение: Пусть 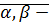 действителные числа, их произведением называется действительное число, которое определяется следующим образом:
действителные числа, их произведением называется действительное число, которое определяется следующим образом:
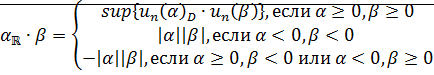
Теорема: Множество 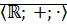 является кольцом. Умножение на
является кольцом. Умножение на 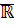 согласуется с умножением на
согласуется с умножением на 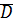 .
.
Доказательство:
1. для сложения всё уже доказано
2. Умножение – б. а. о.

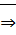 множество
множество 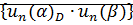 ограничено сверху
ограничено сверху 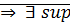 этого множества.
этого множества.
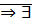 и единственным образом определено умножение неотрицательных действ-ых чисел.
и единственным образом определено умножение неотрицательных действ-ых чисел.
Следовательно, определено умножение действительных чисел.
3. ассоциативность: доказательство достаточно провести для неотрицательных чисел, потому что для других чисел это следует из этого случая:
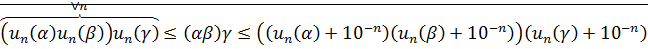 <
<
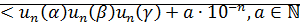
Аналогично:
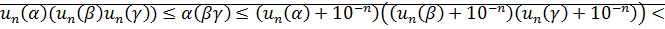
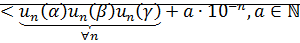
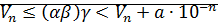
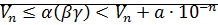
согласно следствию теоремы о плотности множества D в множестве 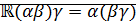
4. дистрибутивность 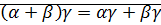 – это равенство очевидно, если одно из чисел
– это равенство очевидно, если одно из чисел 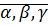 равно
равно 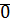 , или
, или 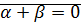 .
.
Достаточно доказать дистрибутивность для 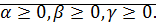 Доказательство аналогично доказательству для ассоциативности. ⊠
Доказательство аналогично доказательству для ассоциативности. ⊠
Теорема: 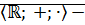 поле.
поле.
Доказательство: достаточно доказать, что если 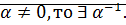
Будем считать, что 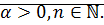 Тогда
Тогда 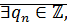 что
что 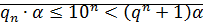
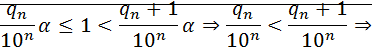
последовательность 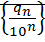 ограниченасверху
ограниченасверху 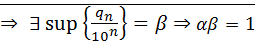 ⊠
⊠
Теорема: Множество действительных чисел содержит множество рациональных чисел. Отношение «=», отношение порядка, операции умножения и сложения на множестве 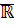 согласуются с соответствующими операциями на множестве
согласуются с соответствующими операциями на множестве 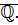
Доказательство: Множество 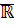 содержит множество
содержит множество 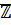 , поэтому мн-во
, поэтому мн-во 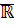 содержит мн-во чисел вида
содержит мн-во чисел вида 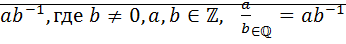 ⊠
⊠
Определение, свойства и алгебраические операции с комплексными числами. Действия над комплексными числами в алгебраической и тригонометрической формах. Вложение поля действительных чисел в поле комплексных чисел
Определение: Системой комплексных чисел называется множество 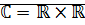 с операциями сложение и умножение:
с операциями сложение и умножение:
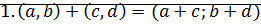 ;
; 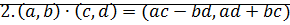 .
.
Теорема: Система комплексных чисел 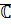 является полем.
является полем.
Доказательство:
1. Сложение коммут-но, ассоц-но, нулевой элемент 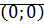 ; противоположный
; противоположный 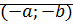 .
.
2. Умножение коммутативно, ассоциативно, единица 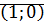 ;
;
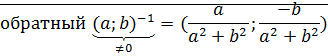
3. дистрибутивность ⊠
Обозначим 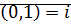 – называется комплексной единицей.
– называется комплексной единицей. 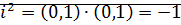 .
. 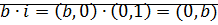 . Поэтому
. Поэтому 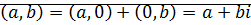 .
.
Определение: Комплексное число 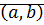 записанное в виде
записанное в виде 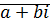 называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Утверждение: Сложение и умножение комплексных чисел в алгебраической форме:
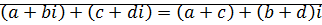 ;
;
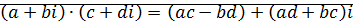 ;
;
Доказательство:
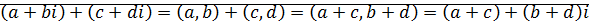 .
.
Аналогично для умножения. ⊠
Замечание: Рассмотрим пару 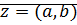 . Поставим в соответствие числа на декартовой плоскости с координатами
. Поставим в соответствие числа на декартовой плоскости с координатами 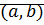 .
.
Длина вектора 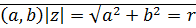
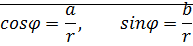
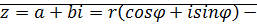 эта форма записи комплексного числа называется тригонометрической.
эта форма записи комплексного числа называется тригонометрической.
Утверждение: Умножение комплексных чисел в тригонометрической форме:
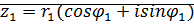 ;
; 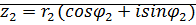 ,
,
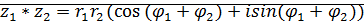 .
.
Утверждение: Если 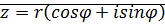 ,
, 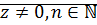 , то
, то 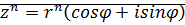 .
.
Определение: Корнем -ой степени из компл. числа 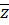 назыв. такое число
назыв. такое число 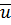 , что
, что 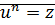 .
.
Обозначение: 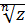 .
.
Теорема: Пусть 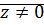 - комплексное число, тогда
- комплексное число, тогда 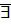 ровно
ровно 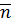 значений корня -ой степени из
значений корня -ой степени из 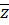 и они находятся по формуле:
и они находятся по формуле:
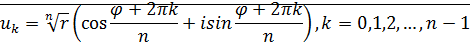
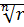 - арифметическое значение корня.
- арифметическое значение корня.
Следствие: Корни степени 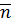 из
из 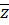 находятся в вершинах правильного -ка.
находятся в вершинах правильного -ка.
Следствие: Мн-во 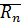 всех корней степени
всех корней степени 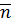 из 1 является мультипликативной группой.
из 1 является мультипликативной группой.
Доказательство:
· 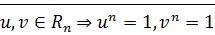
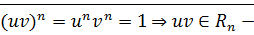 бинарная алгебраическая операция
бинарная алгебраическая операция
· 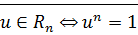
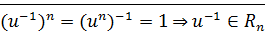
· 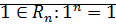 ⊠
⊠



 . Суммой чисел
. Суммой чисел 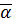 и
и  называется действительное число
называется действительное число 
 является аддитивной абелевой упорядоченной архимедовой группой. Сложение на
является аддитивной абелевой упорядоченной архимедовой группой. Сложение на  согласуется со сложением на
согласуется со сложением на 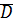 .
.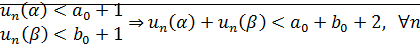
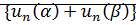 ограничено сверху и поэтому
ограничено сверху и поэтому 
 – рациональные числа(конечные десятичные дроби), а сложение рац. чисел коммутативно.
– рациональные числа(конечные десятичные дроби), а сложение рац. чисел коммутативно. , на
, на 






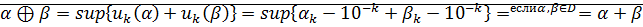






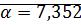


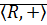 упорядоченная группа.
упорядоченная группа. 



 ⊠
⊠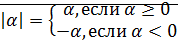
 действителные числа, их произведением называется действительное число, которое определяется следующим образом:
действителные числа, их произведением называется действительное число, которое определяется следующим образом: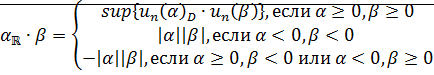
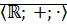 является кольцом. Умножение на
является кольцом. Умножение на 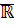 согласуется с умножением на
согласуется с умножением на 
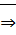 множество
множество 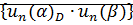 ограничено сверху
ограничено сверху 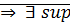 этого множества.
этого множества.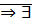 и единственным образом определено умножение неотрицательных действ-ых чисел.
и единственным образом определено умножение неотрицательных действ-ых чисел.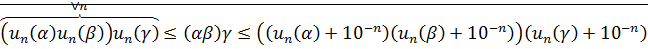 <
<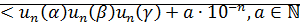
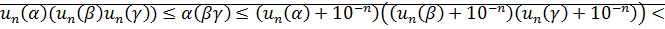
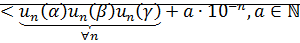
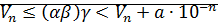
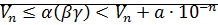
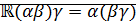
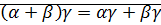 – это равенство очевидно, если одно из чисел
– это равенство очевидно, если одно из чисел 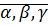 равно
равно 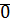 , или
, или 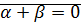 .
.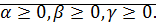 Доказательство аналогично доказательству для ассоциативности. ⊠
Доказательство аналогично доказательству для ассоциативности. ⊠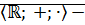 поле.
поле.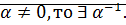
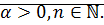 Тогда
Тогда 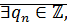 что
что 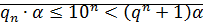
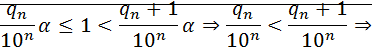
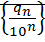 ограниченасверху
ограниченасверху 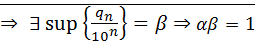 ⊠
⊠
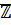 , поэтому мн-во
, поэтому мн-во 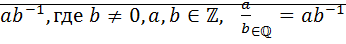 ⊠
⊠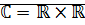 с операциями сложение и умножение:
с операциями сложение и умножение: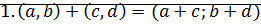 ;
; 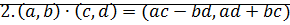 .
.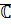 является полем.
является полем.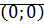 ; противоположный
; противоположный 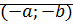 .
.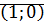 ;
;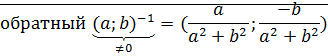
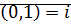 – называется комплексной единицей.
– называется комплексной единицей. 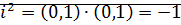 .
. 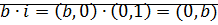 . Поэтому
. Поэтому 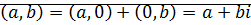 .
.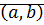 записанное в виде
записанное в виде 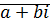 называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.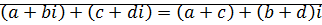 ;
;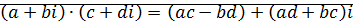 ;
;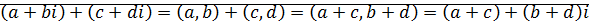 .
.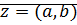 . Поставим в соответствие числа на декартовой плоскости с координатами
. Поставим в соответствие числа на декартовой плоскости с координатами 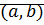 .
.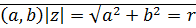
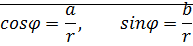
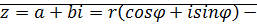 эта форма записи комплексного числа называется тригонометрической.
эта форма записи комплексного числа называется тригонометрической.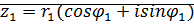 ;
; 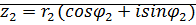 ,
,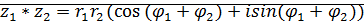 .
.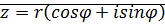 ,
, 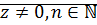 , то
, то 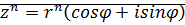 .
.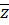 назыв. такое число
назыв. такое число 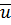 , что
, что 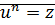 .
.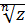 .
.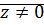 - комплексное число, тогда
- комплексное число, тогда 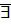 ровно
ровно 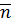 значений корня -ой степени из
значений корня -ой степени из 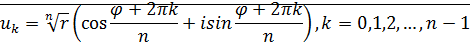
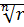 - арифметическое значение корня.
- арифметическое значение корня.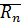 всех корней степени
всех корней степени 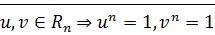
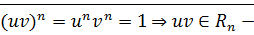 бинарная алгебраическая операция
бинарная алгебраическая операция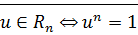
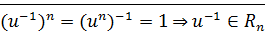
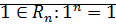 ⊠
⊠
