Материал к зачёту по математике
Студентки 1 курса 117 группы
педиатрического факультета
Аристовой Ольги Николаевны
Билет 1. Случайное событие. Определение вероятности (статистическое и классическое). Понятие о совместных и несовместных событиях, зависимых и независимых событиях.
Случайное событие – событие, которое в данных условиях может произойти, а может не произойти
Статистическое определение вероятности – это предел, к которому стремится относительная частота появления данного события при неограниченном возрастании числа испытаний.
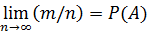
Классическое определение вероятности – это отношение числа ожидаемых событий к полному числу возможных в данном опыте событий.
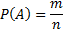
Совместимые события – это события, появление одного из которых не исключает появление другого.
Несовместимые события - это события, появление одного из которых исключает появление другого.
Зависимое событие – это событие, на вероятность которого оказывает влияние исход другого события.
Независимое событие – это событие, на вероятность которого не влияет исход другого события.
Билет 2. Теоремы сложения вероятностей для несовместных и совместных событий.
Теорема сложения вероятностей для несовместных событий:
Вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей.

Теорема сложения вероятностей для совместных событий:
Вероятность появления хотя бы одного из нескольких совместных событий равна сомме их вероятностей без вероятности их совместного появления.

Билет 3. Теоремы умножения вероятностей для независимых и зависимых событий. Условные вероятности.
Теорема умножения вероятностей для независимых событий:
Вероятность совместного появления независимых событий равна произведению их вероятностей. 
Теорема умножения вероятностей для зависимых событий:
Вероятность появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже наступили.

Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло.
Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).
Билет 5. Распределение дискретных случайных величин, их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение (формулы, пояснения).
Случайная величина – это величина, значение которой может быть различным в зависимости от случайных обстоятельств.
Если случайная величина принимает конечное счетное значение х1, х2,..., которым сопоставляется n значений вероятностей:Р(х1), Р(х2) и т.д., то распределение называется дискретным, а случайную величину – дискретной.
Билет 6. Непрерывные и дискретные случайные величины. Закон распределения Бернулли. Формулы для математического ожидания и дисперсии. Примеры.
Случайная величина – это величина, значение которой может быть различным в зависимости от случайных обстоятельств.
Случайная величина называется дискретной, если она принимает счетное множество значений(число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека).
Непрерывная случайная величина принимает любые значения внутри некоторого интервала(температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы).
Билет 7. Непрерывные и дискретные случайные величины. Закон распределения Пуассона. Формулы для математического ожидания и дисперсии. Примеры.
Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения. Например, время, масса, объем.
Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.
Распределение Пуассона применяется, когда вероятность появления события очень мала и исчисляется сотыми или тысячными долями единицы.

Где m -число ожидаемых событий, Pn(m)-вероятность появления m искомых событий в серии из n независимых испытаний, а -наивероятнейшая частота появления ожидаемого события, е -основание натурального логарифма.
Билет 8. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры.
Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения. Например, время, масса, объем.
Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.
Плотность вероятности: для непрерывных случайных величина вероятность p(x) всегда равна нулю, поскольку количество возможных численных значений величины х в любом конечном интервале её изменения бесконечно велико. В связи с этим, для непрерывных случайных величин введена дополнительная характеристика – плотность вероятность.  (x) (ро). Она определяется как производная вероятность по величине х:
(x) (ро). Она определяется как производная вероятность по величине х:

Тогда, используя представление об определённом интеграле, можно выразить вероятность попадания случайной величины в некоторый интервал a<x<b, как

Нормальный закон распределения характеризуется тем, что для него среднее арифметическое значение случайной величины является наиболее вероятным.
формула нормального распределения Гаусса
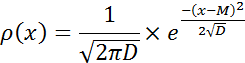
где М - математическое ожидание случайной величины, D - дисперсия;, х – значение величины
 График нормального распределения
График нормального распределения
Точечная оценка.



 Из генеральной совокупности производятся разные выборки одинакового объёма, равнымn. Их выборочные средние x1, x2, x3,..., xi,... являются случайными величинами, распределёнными по нормальному закону, их математическое ожидание равно математическому ожиданию генеральной совокупности, т.е. генеральной средней:
Из генеральной совокупности производятся разные выборки одинакового объёма, равнымn. Их выборочные средние x1, x2, x3,..., xi,... являются случайными величинами, распределёнными по нормальному закону, их математическое ожидание равно математическому ожиданию генеральной совокупности, т.е. генеральной средней:
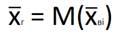
При достаточно большой выборке за генеральную среднюю приближённо принимают выборочную среднюю, математическое ожидание дисперсий и среднее квадратическое отклонение различных выборок, составленных из генеральной совокупности, при больших объёмах выборок приближённо равно генеральной дисперсии и генеральному среднему квадратическому отклонению соответственно.
Интервальная оценка
Интервальной оценкой генеральной средней пользуются при небольшом объёме выборки.
В этом случае указывается интервал (доверительный интервал), в котором с определённой (доверительной) вероятностью p находится генеральная средняя. Доверительная вероятность определяет вероятность, с которой генеральная средняя попадает в интервал:
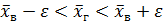
Где положительное число e (эпсилон) характеризует точность оценки.
Наиболее часто p принимает интервалы 0,95; 0,99; 0,999. Чем больше p, тем шире интервал, тем больше e.
Для выборок небольшого объёма в выражении доверительного интервала точность оценки определяется по формуле:
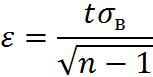
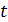 – коэффициент Стьюдента,
– коэффициент Стьюдента, 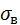 – среднее квадратическое выборки
– среднее квадратическое выборки
Соответственно, подставив данное выражение в неравенство
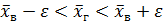
получаем общий вид интервала для генеральной средней в доверительной вероятности
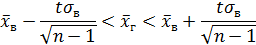
Билет 12. Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя). Примеры.
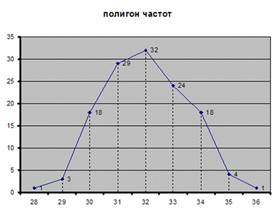
Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (x1; n1), (x2;n2).
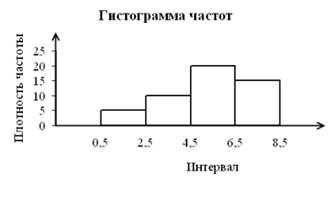
Гистограмма частот – совокупность смежных прямоугольников, построенных на одной прямой линии, основания прямоугольников одинаковы и равны a, а высоту равны отношению частоты к a.
Наиболее распространёнными характеристиками статистического распределения являются средние величины: мода, медиана и выборочная средняя.
Медиа́на — равна варианте, которая расположена в середине статистического распределения, делит статистический ряд на два равные части.
Мода – равна варианте, которой соответствует наибольшая частота.
Выборочная средняя – определяется как среднее арифметическое значение вариант статистического ряда.
Билет 13. Прямые и косвенные измерения. Погрешности измерений. Абсолютная и относительная погрешности измерений. Систематическая, приборная, грубая, случайная погрешности. Примеры.
При прямом измерении числовые значения искомой величины получаются непосредственным сравнением её с мерой (пример – измерение температуры тела медицинским термометром)
Косвенные измерения – это измерения, которые сводятся к нахождению искомой величины по известной зависимости между нею и непосредственно измеренными величинами (например, определение массы тела при взвешивании с учетом выталкивающей силы, определение вязкости жидкости по скорости падения в ней шарика)
Погрешность измерений - этоколичественная характеристика качества измерений.
 xi = xi – X0
xi = xi – X0
Абсолютная погрешность измерения( x) – это разность между результатом измерения и истинным значением измеряемой величины.
x) – это разность между результатом измерения и истинным значением измеряемой величины.
Качество измерений характеризуется относительной погрешностью, которая показывает процентную долю погрешности от истинного значения измеряемой величины
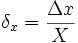 * 100%
* 100%
В величины погрешностей измерений дают вклад несколько различных источников. Им соответствуют, так называемые, грубые, систематические, инструментальные (приборные) и случайные погрешности.
Грубые погрешности – резко изменяют результат измерения и возникают в результате промахов, допускаемых персоналом и неконтролируемых резких изменений в условиях измерений.
Систематические погрешности – имеют постоянные по величине и знаку значения, в ходе всей серии повторных измерений и возникают в результате дефектов измерительных приборов или нарушения методики измерений.
Приборные погрешности – являются характеристикой любого измерительного инструмента и не могу быть равны нулю
Случайные погрешности – являются следствием непредсказуемых статических процессов и объекте измерения, и измерительном приборе, а также случайныхизмерений в условиях проведения опыта. (например, показания электронного термометра, измеряющего температуру воздуха будут варьировать в результате конвекции, вариаций напряжения питания датчика температуры.)
Билет 14. Методы оценки приборной и случайной погрешностей. Коэффициент Стьюдента. Методы оценки косвенных измерений. Примеры.
Для оценки приборных и случайных погрешностей нужно предварительно исключить грубые и систематические погрешности. Случайные погрешности подчиняются нормальному распределению. Искомый результат оказывается в доверительном интервале

 X0 = x + S
X0 = x + S 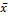 - когда a = 68% (a – доверительный интервал)
- когда a = 68% (a – доверительный интервал)

 X0 = x + 2S
X0 = x + 2S 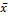 – когда a = 95%
– когда a = 95%

 X0 = x + 3S
X0 = x + 3S 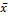 – когда а = 99,7%
– когда а = 99,7%
При малом объёме выборки (5,4,3 измерения) доверительные интервалы для результатов измерений определяют по формуле:
 X0 = x + tanSx, где tan – коэффициент Стьюдента для различных a – доверительных вероятностей, n – числа повторных измерений. Sx - среднее квадратическое среднего арифметического выборки.
X0 = x + tanSx, где tan – коэффициент Стьюдента для различных a – доверительных вероятностей, n – числа повторных измерений. Sx - среднее квадратическое среднего арифметического выборки.
Если учесть вклад инструментальной (приборной) погрешности, то общая погрешность будет равна квадратному корню из суммы квадратов случайной и приборной погрешностей.
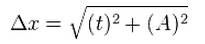 (брать из методичкиМонича и Малиновской, с. 115 внизу)
(брать из методичкиМонича и Малиновской, с. 115 внизу)
Методы оценки косвенных измерений:
Погрешность косвенных измерений определяется как корень из суммы квадратов частных производных по прямо измеряемым величинам, помноженных на погрешности измеряемых величин.
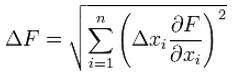 (брать с. 117 методичкаМонича и Малиновской)
(брать с. 117 методичкаМонича и Малиновской)
Пример – в ходе одной из лабораторных работ были определены погрешности косвенных измерений импеданса живой ткани на разных частотах.
Материал к зачёту по математике
Студентки 1 курса 117 группы
педиатрического факультета
Аристовой Ольги Николаевны



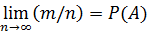
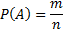





 (x) (ро). Она определяется как производная вероятность по величине х:
(x) (ро). Она определяется как производная вероятность по величине х:

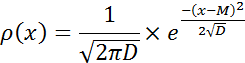
 График нормального распределения
График нормального распределения


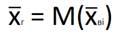
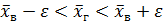
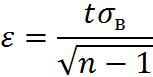
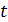 – коэффициент Стьюдента,
– коэффициент Стьюдента, 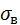 – среднее квадратическое выборки
– среднее квадратическое выборки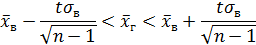


 xi = xi – X0
xi = xi – X0 x) – это разность между результатом измерения и истинным значением измеряемой величины.
x) – это разность между результатом измерения и истинным значением измеряемой величины.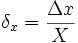 * 100%
* 100%
 X0 = x + S
X0 = x + S 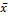 - когда a = 68% (a – доверительный интервал)
- когда a = 68% (a – доверительный интервал)
 X0 = x + 2S
X0 = x + 2S 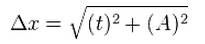 (брать из методичкиМонича и Малиновской, с. 115 внизу)
(брать из методичкиМонича и Малиновской, с. 115 внизу)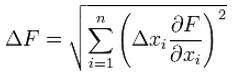 (брать с. 117 методичкаМонича и Малиновской)
(брать с. 117 методичкаМонича и Малиновской)


