Дискретные случайные величины. Законы
Распределения биномиальное, геометрическое и Пуассона.
Опр. Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно.
Опр. Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.  , причем
, причем 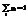 . Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения
. Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения 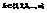 с вероятностями
с вероятностями 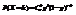 .
.  Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения
Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения  с вероятностями
с вероятностями 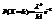 . Обозначают
. Обозначают  , т.е. случайная величина Х имеет распределение Пуассона с параметром λ.
, т.е. случайная величина Х имеет распределение Пуассона с параметром λ.  Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения
Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения 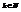 с вероятностями
с вероятностями  , где q=1-p.
, где q=1-p.
 .
.
31. Функция распределения и плотность вероятности непрерывной случайной величины
Если функция распределения Fx (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины px (x), которая связана с функцией распределения Fx (x) формулами
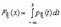 и.
и. 
Отсюда, в частности, следует, что для любой случайной величины. 
Мат ожидание ДСВ и их свойства.
Опр. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Обозначают математическое ожидание случайной величины Х через MX или М(Х).  – случайная величина Х принимает конечное число значений.
– случайная величина Х принимает конечное число значений.  – принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
– принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Свойства математического ожидания:
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: M(C)=C. Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно,  .
.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X).
Ряд распределения случайной величины СХ
Математическое ожидание случайной величины СХ  .
.
Опр. Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn  .
.
Моменты случайной величины
Моме́нтслуча́йной величины́ — числовая характеристика распределения данной случайной величины. Определения
Если дана случайная величина Х определённая на некотором вероятностном пространстве, то:К-мнача́льным моментом случайной величины Х где 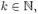 называется величина
называется величина 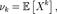 если математическое ожидание
если математическое ожидание 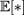 в правой части этого равенства определено; К-м центра́льным моментом случайной величины называется величина
в правой части этого равенства определено; К-м центра́льным моментом случайной величины называется величина
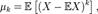 К-м абсолю́тным и К -м центральным абсолютным моментами случайной величины называется соответственно величины
К-м абсолю́тным и К -м центральным абсолютным моментами случайной величины называется соответственно величины 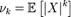 и
и 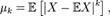 К-м факториальным моментом случайной величины Х называется величина
К-м факториальным моментом случайной величины Х называется величина 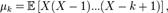
если математическое ожидание в правой части этого равенства определено.
Абсолютные моменты могут быть определены не только для целых k, но и для любых положительных действительных в случае, если соответствующие интегралы сходятся.
Ковариация.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции.
Опр. Ковариацией между случайными величинами Х и Y называется число 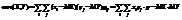 , где
, где 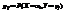 .Для непрерывных случайных величин X и Y используют формулу
.Для непрерывных случайных величин X и Y используют формулу 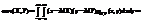
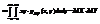 . Покажем, что если случайные величины Х и Y независимы, то
. Покажем, что если случайные величины Х и Y независимы, то 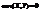 . Пусть Х и Y—непрерывные случайные величины
. Пусть Х и Y—непрерывные случайные величины 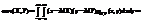
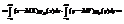
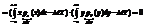
Ф.мног.слювел.
Функцией распределения n-мерной случайной величиной (Х1, Х2, …, Хn)
называется вероятность выполнения n неравенств вида Хi < xi:

Закон больших чисел.
Вариационный ряд.
Множество всех вариант выборки, расположенных в порядке возрастания их значений, вместе с их соответствующими частотами или относительными частотами называется вариационным рядом:
Таблица интервалов, содержащая данную выборку значений случайной величины Х и соответствующие частоты или относительные частоты, называется статистическим рядом. Статистический ряд распределения вероятностей определяется по
исходной выборке объемом n, если анализируемая случайная величина Х является дискретной с известным множеством значений {x1..xm }:

Гистограмма – статистический аналог графика плотности вероятности f *(x) случайной величины, и она строится по интервальному статистическомуряду. Гистограмма представляет собой совокупность прямоугольников, построенных, как на основаниях, на интервалах hj статистического ряда с высотой равной статистической плотности вероятности в соответствующем
Эпмирическая функция.
Если x 1, x 2, … x n – выборка значений случайной величины Х, то эмпирической функцией распределения называется функция действительного аргумента x Î (- ∞; ∞), обозначаемая через  , равная относительной частоте выборочных значений, меньших числа x.
, равная относительной частоте выборочных значений, меньших числа x.
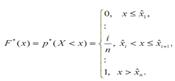
Так как относительная частота значений случайной величины Х, удовлетворяющих неравенству Х < x, в выборке объема n стремится к вероятности выполнения этого неравенства, то при n → ∞ имеем, что  =
=  → P(X < x) = Fх(x).
→ P(X < x) = Fх(x).
Эмпирическая функция распределения обладает всеми свойствами теоретической функции распределения.
1. Эмпирическая функция распределения является неубывающей функцией, то есть 

 при x 1 < x 2.
при x 1 < x 2.
2. Справедливы следующие равенства:


 и
и 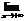
 .
.
3. Все значения эмпирической функции распределения находятся между 0 и 1, то есть
Выборочное среднее
Пусть  — выборка из распределения вероятности, определённая на некотором вероятностном пространстве
— выборка из распределения вероятности, определённая на некотором вероятностном пространстве  . Тогда её выборочным средним называется случайная величина
. Тогда её выборочным средним называется случайная величина
 .
.
Выборочная дисперсия
Пусть  — выборка из распределения вероятности. Тогда
— выборка из распределения вероятности. Тогда
Выборочная дисперсия — это случайная величина
 ,
,
где символ  обозначает выборочное среднее.
обозначает выборочное среднее.
Несмещённая (исправленная) дисперсия — это случайная величина
 .
.
50. Распределение  (хи-квадрат) с
(хи-квадрат) с  степенями свободы — это распределение суммы квадратов
степенями свободы — это распределение суммы квадратов  независимых стандартных нормальных случайных величин. Пусть
независимых стандартных нормальных случайных величин. Пусть 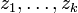 — совместно независимые стандартные нормальные случайные величины, то есть:
— совместно независимые стандартные нормальные случайные величины, то есть:  . Тогда случайная величина
. Тогда случайная величина

имеет распределение хи-квадрат с  степенями свободы, то есть
степенями свободы, то есть  .
.
Распределение хи-квадрат является частным случаем гамма - распределения, и имеет вид:
 ,
,
где  означает Гамма-распределение, а
означает Гамма-распределение, а  — Гамма-функцию.
— Гамма-функцию.
Функция распределения имеет следующий вид:
 ,
,
где 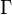 и
и  обозначают соответственно полную и неполную гамма-функции.
обозначают соответственно полную и неполную гамма-функции.
51 Распределе́ниеСтью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма СилиГоссета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент». Пусть  — независимыестандартные нормальные случайные величины, такие что
— независимыестандартные нормальные случайные величины, такие что  . Тогда распределение случайной величины
. Тогда распределение случайной величины  , где
, где

называется распределением Стьюдента с  степенями свободы. Пишут
степенями свободы. Пишут  . Её распределение абсолютно непрерывно и имеет плотность
. Её распределение абсолютно непрерывно и имеет плотность
 ,
,
где  — гамма-функция Эйлера.
— гамма-функция Эйлера.
52 Распределе́ниеФи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Пусть  — две независимые случайные величины, имеющие распределение хи-квадрат:
— две независимые случайные величины, имеющие распределение хи-квадрат:  , где
, где  . Тогда распределение случайной величины
. Тогда распределение случайной величины
, 
называется распределением Фишера (распределением Снедекора) со степенями свободы  и
и  . Пишут
. Пишут  .
.
Дискретные случайные величины. Законы



 , причем
, причем 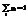 . Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения
. Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения 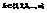 с вероятностями
с вероятностями 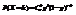 .
.  Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения
Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения  с вероятностями
с вероятностями 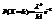 . Обозначают
. Обозначают  , т.е. случайная величина Х имеет распределение Пуассона с параметром λ.
, т.е. случайная величина Х имеет распределение Пуассона с параметром λ.  Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения
Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения 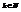 с вероятностями
с вероятностями  , где q=1-p.
, где q=1-p. .
.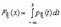 и.
и. 

 – случайная величина Х принимает конечное число значений.
– случайная величина Х принимает конечное число значений.  – принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
– принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. .
. .
. .
.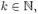 называется величина
называется величина 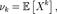 если математическое ожидание
если математическое ожидание 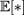 в правой части этого равенства определено; К-м центра́льным моментом случайной величины называется величина
в правой части этого равенства определено; К-м центра́льным моментом случайной величины называется величина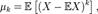 К-м абсолю́тным и К -м центральным абсолютным моментами случайной величины называется соответственно величины
К-м абсолю́тным и К -м центральным абсолютным моментами случайной величины называется соответственно величины 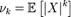 и
и 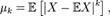 К-м факториальным моментом случайной величины Х называется величина
К-м факториальным моментом случайной величины Х называется величина 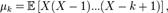
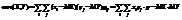 , где
, где 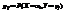 .Для непрерывных случайных величин X и Y используют формулу
.Для непрерывных случайных величин X и Y используют формулу 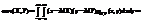
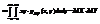 . Покажем, что если случайные величины Х и Y независимы, то
. Покажем, что если случайные величины Х и Y независимы, то 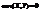 . Пусть Х и Y—непрерывные случайные величины
. Пусть Х и Y—непрерывные случайные величины 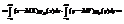
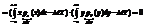



 …
… 


 …
… 


 …
… 

 , равная относительной частоте выборочных значений, меньших числа x.
, равная относительной частоте выборочных значений, меньших числа x.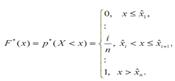
 =
=  → P(X < x) = Fх(x).
→ P(X < x) = Fх(x).

 при x 1 < x 2.
при x 1 < x 2.

 и
и 
 .
. — выборка из распределения вероятности, определённая на некотором вероятностном пространстве
— выборка из распределения вероятности, определённая на некотором вероятностном пространстве  . Тогда её выборочным средним называется случайная величина
. Тогда её выборочным средним называется случайная величина .
. — выборка из распределения вероятности. Тогда
— выборка из распределения вероятности. Тогда ,
, обозначает выборочное среднее.
обозначает выборочное среднее. .
. (хи-квадрат) с
(хи-квадрат) с  степенями свободы — это распределение суммы квадратов
степенями свободы — это распределение суммы квадратов 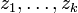 — совместно независимые стандартные нормальные случайные величины, то есть:
— совместно независимые стандартные нормальные случайные величины, то есть:  . Тогда случайная величина
. Тогда случайная величина
 .
. ,
, означает Гамма-распределение, а
означает Гамма-распределение, а  — Гамма-функцию.
— Гамма-функцию. ,
,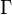 и
и  обозначают соответственно полную и неполную гамма-функции.
обозначают соответственно полную и неполную гамма-функции. — независимыестандартные нормальные случайные величины, такие что
— независимыестандартные нормальные случайные величины, такие что  . Тогда распределение случайной величины
. Тогда распределение случайной величины  , где
, где
 степенями свободы. Пишут
степенями свободы. Пишут  . Её распределение абсолютно непрерывно и имеет плотность
. Её распределение абсолютно непрерывно и имеет плотность ,
, — гамма-функция Эйлера.
— гамма-функция Эйлера. — две независимые случайные величины, имеющие распределение хи-квадрат:
— две независимые случайные величины, имеющие распределение хи-квадрат:  , где
, где  . Тогда распределение случайной величины
. Тогда распределение случайной величины
 и
и  . Пишут
. Пишут  .
.

