Способ расчёта смешанного произведения векторов чисто алгебраический:
Смешанное произведение векторов 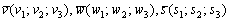 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 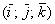 правой ориентации, выражается формулой:
правой ориентации, выражается формулой:

Определение, строго говоря, неполное, но в теоретические тонкости вникать не будем, правая ориентация базиса – это его «нормальная» ориентация, в которой мы будем решать практические задачи. Вполне достаточно.
Как и для векторного произведения, координаты векторов следует «укладывать» в определитель в строгом порядке. Если в смешанном произведении  выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.
выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.
Следует отметить, что координаты векторов не обязательно записывать в строки, их можно записать и в столбцы – слева направо, и тоже в строгом порядке:

Значение определителя от этого не изменится.
Второй важный момент касается компланарности векторов. Как уже отмечалось, если векторы 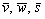 компланарны, то
компланарны, то 
Такое задание уже было!
Пример 11
Даны векторы  .
.
Вычислить:
а) смешанное произведение векторов;
б) объём параллелепипеда, построенного на векторах  ;
;
в) объём тетраэдра, построенного на векторах  .
.
Решение: Всё быстро и просто:
а) По формуле смешанного произведения:

(Определитель раскрыт по первому столбцу)
б) Объём параллелепипеда, построенного на векторах  , равен модулю смешанного произведения данных векторов:
, равен модулю смешанного произведения данных векторов:

в) Вычислим объём тетраэдра, построенного на данных векторах:

Ответ: 
В пункте а) тоже можно было добавить размерность «кубические единицы», но здесь к объёму добавляется знак «минус», поэтому смотреться будет всё-таки не очень.
На практике, по моей субъективной оценке, в 95-99% случаев требуется вычислить объём треугольной пирамиды:
Пример 12
Вычислить объём треугольной пирамиды, если даны её вершины 
Решение: рекомендую выполнить схематический рисунок пирамидки, чтобы лучше понять суть проводимых действий.
Сначала найдём векторы:

Вычислим смешанное произведение:

(Определитель раскрыт по первой строке)
Вычислим объём треугольной пирамиды  :
:

Ответ: 
Рассмотренная задача имеет не единственное решение, можно было взять и другую группу векторов, начиная движение от любой другой вершины пирамиды. Чем-то похоже на задачу предыдущей части урока о площади треугольника.
Объём тетраэдра – хит смешанного произведения, поэтому заключительный счастливый номер пусть будет таким же:
Пример 13
Вычислить объём пирамиды, заданной вершинами 
Это пример для самостоятельного решения. В образце решения рассмотрены векторы, отложенные от «традиционной» точки  .
.
Решения и ответы:
Пример 2: Решение: По соответствующей формуле:

Ответ: 
Пример 5: Решение:
1) Выразим вектор  через вектор
через вектор  :
:

2) Вычислим длину векторного произведения:

Ответ: 
Пример 7: Решение: 1) Найдём векторное произведение:

2) Вычислим длину векторного произведения:

Ответ: 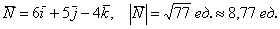
Пример 9: Решение: Найдём вектор:
 .
.
Векторное произведение:

Площадь параллелограмма:

Ответ: 
Пример 13: Решение: Найдём векторы:

Вычислим смешанное произведение:

(Определитель раскрыт по первой строке)
Вычислим объём пирамиды  :
:

Ответ: 
Формулы деления отрезка в данном отношении.
Формулы координат середины отрезка
Понятие деления отрезка в данном отношении
Нередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек  и, очевидное невероятное – отрезок
и, очевидное невероятное – отрезок  :
:

Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок  делится на две части с помощью некоторой точки
делится на две части с помощью некоторой точки  , которая, понятно, расположена прямо на нём:
, которая, понятно, расположена прямо на нём:

В данном примере точка  делит отрезок
делит отрезок  ТАКИМ образом, что отрезок
ТАКИМ образом, что отрезок  в два раза короче отрезка
в два раза короче отрезка  . ЕЩЁ можно сказать, что точка
. ЕЩЁ можно сказать, что точка  делит отрезок
делит отрезок  в отношении
в отношении  («один к двум»), считая от вершины
(«один к двум»), считая от вершины 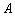 .
.
На сухом математическом языке этот факт записывают следующим образом:  , или чаще в виде привычной пропорции:
, или чаще в виде привычной пропорции:  . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае:
. Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае:  .
.
Пропорцию несложно составить и в другом порядке:  – сия запись означает, что отрезок
– сия запись означает, что отрезок  в два раза длиннее отрезка
в два раза длиннее отрезка  , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
, но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение:  . Если составить пропорцию наоборот, тогда получаем:
. Если составить пропорцию наоборот, тогда получаем:  .
.
После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.
Формулы деления отрезка в данном отношении на плоскости
Если известны две точки плоскости  , то координаты точки
, то координаты точки  , которая делит отрезок
, которая делит отрезок  в отношении
в отношении  , выражаются формулами:
, выражаются формулами:

Такая вот универсальная задача.
Пример 1
Найти координаты точки 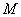 , делящей отрезок
, делящей отрезок  в отношении
в отношении  , если известны точки
, если известны точки 
Решение: В данной задаче  . По формулам деления отрезка в данном отношении, найдём точку
. По формулам деления отрезка в данном отношении, найдём точку  :
:

Ответ: 
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.
В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:

Действительно, соотношение  выполняется, то есть отрезок
выполняется, то есть отрезок  в три раза короче отрезка
в три раза короче отрезка  . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
. Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Равноценен второй способ решения: в нём отсчёт начинается с точки  и справедливым является отношение:
и справедливым является отношение:  (человеческими словами, отрезок
(человеческими словами, отрезок  в три раза длиннее отрезка
в три раза длиннее отрезка  ). По формулам деления отрезка в данном отношении:
). По формулам деления отрезка в данном отношении:

Ответ: 
Заметьте, что в формулах необходимо переместить координаты точки  на первое место, поскольку маленький триллер начинался именно с неё.
на первое место, поскольку маленький триллер начинался именно с неё.
Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок  , то предполагается, что вы составите пропорцию
, то предполагается, что вы составите пропорцию  , если дан отрезок
, если дан отрезок  , то «негласно» подразумевается пропорция
, то «негласно» подразумевается пропорция  .
.
А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки.
Пример 2
Даны точки  . Найти:
. Найти:
а) точку 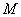 , делящую отрезок
, делящую отрезок  в отношении
в отношении 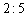 ;
;
б) точку  , делящую отрезок
, делящую отрезок  в отношении
в отношении  .
.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Иногда встречаются задачи, где неизвестен один из концов отрезка:
Пример 3
Точка  принадлежит отрезку
принадлежит отрезку  . Известно, что отрезок
. Известно, что отрезок  в два раза длиннее отрезка
в два раза длиннее отрезка  . Найти точку
. Найти точку  , если
, если  .
.
Решение: Из условия следует, что точка  делит отрезок
делит отрезок  в отношении
в отношении  , считая от вершины
, считая от вершины  , то есть, справедлива пропорция:
, то есть, справедлива пропорция:  . По формулам деления отрезка в данном отношении:
. По формулам деления отрезка в данном отношении:

Сейчас нам неизвестны координаты точки  :
:  , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
, но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
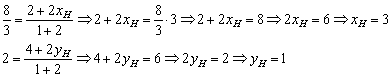
Ответ: 
Для проверки можно взять концы отрезка  и, пользуясь формулами в прямом порядке, убедиться, что при соотношении
и, пользуясь формулами в прямом порядке, убедиться, что при соотношении  действительно получится точка
действительно получится точка  . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
. И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
Пример 4
Точка  . Отрезок
. Отрезок  в полтора раза короче отрезка
в полтора раза короче отрезка  . Найти точку
. Найти точку 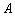 , если известны координат точек
, если известны координат точек  .
.
Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.
Формулы деления отрезка в данном отношении в пространстве
Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.
Если известны две точки пространства  , то координаты точки
, то координаты точки  , которая делит отрезок
, которая делит отрезок  в отношении
в отношении  , выражаются формулами:
, выражаются формулами:
 .
.
Пример 5
Даны точки  . Найти координаты точки
. Найти координаты точки 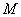 , принадлежащей отрезку
, принадлежащей отрезку  , если известно, что
, если известно, что  .
.
Решение: Из условия следует отношение:  . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость – пропорцию в условии рациональнее было записать так:
. Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость – пропорцию в условии рациональнее было записать так: 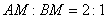 .
.
По формулам координат середины отрезка:

Ответ: 
Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.
Что касается дробей в ответе, не удивляйтесь, обычное дело. В высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде  пойдёт, но вариант с неправильными дробями более стандартен.
пойдёт, но вариант с неправильными дробями более стандартен.
Разминочная задача для самостоятельного решения:
Пример 6
Даны точки  . Найти координаты точки
. Найти координаты точки 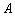 , если известно, что она делит отрезок
, если известно, что она делит отрезок  в отношении
в отношении  .
.
Решение и ответ в конце. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.
Формулы координат середины отрезка
Даже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. 
пропорция  . И общие формулы
. И общие формулы  чудесным образом преображаются в нечто знакомое и простое:
чудесным образом преображаются в нечто знакомое и простое:

Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:

Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка  , то координаты его середины
, то координаты его середины 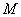 выражаются формулами:
выражаются формулами:

Пример 7
Параллелограмм  задан координатами своих вершин
задан координатами своих вершин  . Найти точку пересечения его диагоналей.
. Найти точку пересечения его диагоналей.
Решение: По известному свойству, диагонали параллелограмма своей точкой пересечения  делятся пополам, поэтому задачу можно решить двумя способами.
делятся пополам, поэтому задачу можно решить двумя способами.
Способ первый: Рассмотрим противоположные вершины 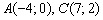 . По формулам деления отрезка пополам найдём середину диагонали
. По формулам деления отрезка пополам найдём середину диагонали 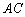 :
:

В результате: 
Способ второй: Рассмотрим противоположные вершины  . По формулам деления отрезка пополам найдём середину диагонали
. По формулам деления отрезка пополам найдём середину диагонали  :
:

Таким образом: 
Ответ: 
Пространственный отрезок для самостоятельного решения:
Пример 8
Даны точки  . Найти середину
. Найти середину  отрезка
отрезка  .
.
Решение в конце.
Пример 9
Точка 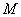 делит отрезок
делит отрезок  пополам. Найти точку
пополам. Найти точку  , если известны точки
, если известны точки 
Решение: Используем формулы координат середины отрезка:

Нам неизвестны координаты 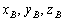 . И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:
. И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:

Ответ: 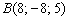
Проверка выполняется даже устно: берём концы отрезка  и находим его середину.
и находим его середину.
Решения и ответы:
Пример 2: Решение:
а)  . Используем формулы деления отрезка в данном отношении:
. Используем формулы деления отрезка в данном отношении:
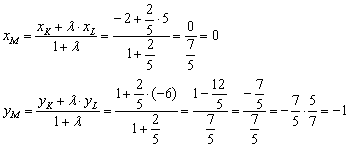
Ответ: 
б) 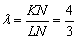 . Используем формулы деления отрезка в данном отношении:
. Используем формулы деления отрезка в данном отношении:
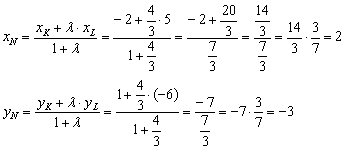
Ответ: 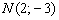
Пример 4: Решение: Используем формулы деления отрезка в данном отношении:

Из условия следует, что  .
.
Примечание: формулировка условия «отрезок  в полтора раза короче отрезка
в полтора раза короче отрезка  » эквивалентна формулировке «отрезок
» эквивалентна формулировке «отрезок  в полтора раза длиннее отрезка
в полтора раза длиннее отрезка  », именно из этих соображений и составлена пропорция.
», именно из этих соображений и составлена пропорция.
По условию  , таким образом:
, таким образом:

Ответ: 
Пример 6: Решение: Используем формулы деления отрезка в данном отношении:

В данной задаче  .
.
Таким образом:

Ответ: 
Пример 8: Решение: Используем формулы координат середины отрезка:
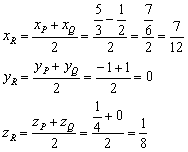
Ответ: 
Уравнение прямой на плоскости.
Направляющий вектор прямой. Вектор нормали
Прямая линия на плоскости – это одна из простейших геометрических фигур. Для освоения материала необходимо уметь строить прямую; знать, каким уравнением задаётся прямая, в частности, прямая, проходящая через начало координат и прямые, параллельные координатным осям.
Мы рассмотрим способы, с помощью которых можно составить уравнение прямой на плоскости. Рекомендую не пренебрегать практическими примерами (даже если кажется очень просто), так как я буду снабжать их элементарными и важными фактами, техническими приёмами, которые потребуются в дальнейшем, в том числе и в других разделах высшей математики.
Уравнение прямой с угловым коэффициентом
Всем известный «школьный» вид уравнения прямой  называется уравнением прямой с угловым коэффициентом
называется уравнением прямой с угловым коэффициентом  . Например, если прямая задана уравнением
. Например, если прямая задана уравнением  , то её угловой коэффициент:
, то её угловой коэффициент:  . Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:
. Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси  и данной прямой:
и данной прямой:  , причём угол
, причём угол  «откручивается» против часовой стрелки.
«откручивается» против часовой стрелки.
Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых. Рассмотрим «красную» прямую  и её угловой коэффициент
и её угловой коэффициент  . Согласно вышесказанному:
. Согласно вышесказанному:  (угол «альфа» обозначен зелёной дугой). Для «синей» прямой
(угол «альфа» обозначен зелёной дугой). Для «синей» прямой  с угловым коэффициентом
с угловым коэффициентом  справедливо равенство
справедливо равенство  (угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс.
(угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс.
При этом возможны следующие случаи:
1) Если угловой коэффициент отрицателен: 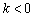 , то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.
, то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.
2) Если угловой коэффициент положителен: 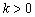 , то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.
, то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.
3) Если угловой коэффициент равен нулю:  , то уравнение
, то уравнение  принимает вид
принимает вид  , и соответствующая прямая параллельна оси
, и соответствующая прямая параллельна оси  . Пример – «жёлтая» прямая.
. Пример – «жёлтая» прямая.
4) Для семейства прямых 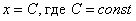 , параллельных оси
, параллельных оси  (на чертеже нет примера, кроме самой оси
(на чертеже нет примера, кроме самой оси  ), угловой коэффициент не определён. В данной ситуации
), угловой коэффициент не определён. В данной ситуации  , а тангенса угла 90 градусов не существует.
, а тангенса угла 90 градусов не существует.
Чем больше угловой коэффициент по модулю, тем круче идёт график прямой.
Например, рассмотрим две прямые  . Здесь
. Здесь  , поэтому прямая
, поэтому прямая  имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
В свою очередь, прямая  более крутА, чем прямые
более крутА, чем прямые  .
.
Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой.
Для прямых  справедливо неравенство
справедливо неравенство  , таким образом, прямая
, таким образом, прямая  более полога.
более полога.
Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – если на чертеже получилось «явно что-то не то». Желательно, чтобы вам сразу было понятно, что, например, прямая  весьма крутА и идёт снизу вверх, а прямая
весьма крутА и идёт снизу вверх, а прямая  – очень полога, близко прижата к оси
– очень полога, близко прижата к оси  и идёт сверху вниз.
и идёт сверху вниз.
В геометрических задачах часто фигурируют несколько прямых, поэтому их удобно как-нибудь обозначать.
Обозначения: прямые обозначаются маленькими латинскими буквами:  . Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через
. Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через 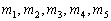 .
.
Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: 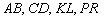 и т.д. Обозначение
и т.д. Обозначение  совершенно очевидно подразумевает, что точки
совершенно очевидно подразумевает, что точки  принадлежат прямой
принадлежат прямой  .
.
Как составить уравнение прямой с угловым коэффициентом?
Если известна точка  , принадлежащая некоторой прямой, и угловой коэффициент
, принадлежащая некоторой прямой, и угловой коэффициент  этой прямой, то уравнение данной прямой выражается формулой:
этой прямой, то уравнение данной прямой выражается формулой:

Пример 1
Составить уравнение прямой с угловым коэффициентом  , если известно, что точка
, если известно, что точка  принадлежит данной прямой.
принадлежит данной прямой.
Решение: Уравнение прямой составим по формуле  . В данном случае:
. В данном случае:

Ответ: 
Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение  и убеждаемся, что наш угловой коэффициент
и убеждаемся, что наш угловой коэффициент  на своём месте. Во-вторых, координаты точки
на своём месте. Во-вторых, координаты точки  должны удовлетворять данному уравнению. Подставим их в уравнение:
должны удовлетворять данному уравнению. Подставим их в уравнение:

Получено верное равенство, значит, точка  удовлетворяет полученному уравнению.
удовлетворяет полученному уравнению.
Вывод: уравнение найдено правильно.
пример для самостоятельного решения:
Пример 2
Составить уравнение прямой, если известно, что её угол наклона к положительному направлению оси  составляет
составляет  , и точка
, и точка  принадлежит данной прямой.
принадлежит данной прямой.
Общее уравнение прямой
Ностальгически машем ручкой привычному  и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно:
и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно:
Общее уравнение прямой имеет вид: 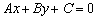 , где
, где 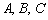 – некоторые числа. При этом коэффициенты
– некоторые числа. При этом коэффициенты  одновременно не равны нулю, так как уравнение теряет смысл.
одновременно не равны нулю, так как уравнение теряет смысл.
Рассмотрим уравнение с угловым коэффициентом  . Сначала перенесём все слагаемые в левую часть:
. Сначала перенесём все слагаемые в левую часть:

Слагаемое с «иксом» нужно поставить на первое место:

В принципе, уравнение уже имеет вид 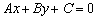 , но по правилам математического этикета коэффициент первого слагаемого (в данном случае
, но по правилам математического этикета коэффициент первого слагаемого (в данном случае 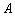 ) должен быть положительным. Меняем знаки:
) должен быть положительным. Меняем знаки:

Готово.
Запомните эту техническую особенность! Первый коэффициент (чаще всего 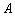 ) делаем положительным!
) делаем положительным!
В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме. Ну, а при необходимости его легко привести к «школьному» виду с угловым коэффициентом  (за исключением прямых, параллельных оси ординат).
(за исключением прямых, параллельных оси ординат).
Направляющий вектор прямой
Зададимся вопросом, что достаточно знать, чтобы построить прямую?
Вектор, который параллелен прямой, называется направляющим вектором данной прямой. Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).
Направляющий вектор я буду обозначать следующим образом:  .
.
Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку  , которая принадлежит прямой.
, которая принадлежит прямой.
Как составить уравнение прямой по точке и направляющему вектору?
Если известна некоторая точка  , принадлежащая прямой, и направляющий вектор
, принадлежащая прямой, и направляющий вектор  этой прямой, то уравнение данной прямой можно составить по формуле:
этой прямой, то уравнение данной прямой можно составить по формуле:

Иногда его называют каноническим уравнением прямой.
Что делать, когда одна из координат  равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.
равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.
Пример 3
Составить уравнение прямой по точке 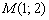 и направляющему вектору
и направляющему вектору 
Решение: Уравнение прямой составим по формуле  . В данном случае:
. В данном случае:

С помощью свойств пропорции избавляемся от дробей:

И приводим уравнение к общему виду:

Ответ: 
Чертежа в таких примерах, как правило, делать не нужно, но понимания ради:

На чертеже мы видим исходную точку 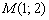 , исходный направляющий вектор
, исходный направляющий вектор  (его можно отложить от любой точки плоскости) и построенную прямую
(его можно отложить от любой точки плоскости) и построенную прямую  . Кстати, во многих случаях построение прямой удобнее всего осуществлять как раз с помощью уравнения с угловым коэффициентом. Наше уравнение
. Кстати, во многих случаях построение прямой удобнее всего осуществлять как раз с помощью уравнения с угловым коэффициентом. Наше уравнение  легко преобразовать к виду
легко преобразовать к виду  и без проблем подобрать ещё одну точку для построения прямой.
и без проблем подобрать ещё одну точку для построения прямой.
Как отмечалось в начале параграфа, у прямой бесконечно много направляющих векторов, и все они коллинеарны. Для примера я нарисовал три таких вектора:  . Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой
. Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой  .
.
Составим уравнение прямой по точке 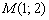 и направляющему вектору
и направляющему вектору  :
:

Разруливаем пропорцию:

Делим обе части на –2 и получаем знакомое уравнение: 
Желающие могут аналогичным образом протестировать векторы  или любой другой коллинеарный вектор.
или любой другой коллинеарный вектор.
Теперь решим обратную задачу:
Как найти направляющий вектор по общему уравнению прямой?
Очень просто:
Если прямая задана общим уравнением 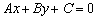 в прямоугольной системе координат, то вектор
в прямоугольной системе координат, то вектор  является направляющим вектором данной прямой.
является направляющим вектором данной прямой.
Примеры нахождения направляющих векторов прямых:

Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить:
Так, уравнение  задаёт прямую, которая параллельна оси
задаёт прямую, которая параллельна оси  и координаты полученного направляющего вектора
и координаты полученного направляющего вектора  удобно разделить на –2, получая в точности базисный вектор
удобно разделить на –2, получая в точности базисный вектор 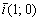 в качестве направляющего вектора. Логично.
в качестве направляющего вектора. Логично.
Аналогично, уравнение  задаёт прямую, параллельную оси
задаёт прямую, параллельную оси  , и, разделив координаты вектора
, и, разделив координаты вектора 
|
|
|





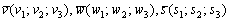 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 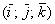 правой ориентации, выражается формулой:
правой ориентации, выражается формулой:
 выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.
выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.
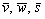 компланарны, то
компланарны, то 
 .
. ;
;






 :
:


 .
.

 через вектор
через вектор  :
: 




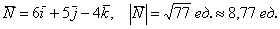
 .
. 




 :
: 

 и, очевидное невероятное – отрезок
и, очевидное невероятное – отрезок  :
:
 , которая, понятно, расположена прямо на нём:
, которая, понятно, расположена прямо на нём:
 в два раза короче отрезка
в два раза короче отрезка  . ЕЩЁ можно сказать, что точка
. ЕЩЁ можно сказать, что точка  («один к двум»), считая от вершины
(«один к двум»), считая от вершины 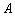 .
. , или чаще в виде привычной пропорции:
, или чаще в виде привычной пропорции:  . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае:
. Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае:  .
. – сия запись означает, что отрезок
– сия запись означает, что отрезок 
 . Если составить пропорцию наоборот, тогда получаем:
. Если составить пропорцию наоборот, тогда получаем:  .
. , то координаты точки
, то координаты точки  , которая делит отрезок
, которая делит отрезок  , выражаются формулами:
, выражаются формулами:
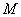 , делящей отрезок
, делящей отрезок  , если известны точки
, если известны точки 
 . По формулам деления отрезка в данном отношении, найдём точку
. По формулам деления отрезка в данном отношении, найдём точку 


 выполняется, то есть отрезок
выполняется, то есть отрезок  и справедливым является отношение:
и справедливым является отношение:  (человеческими словами, отрезок
(человеческими словами, отрезок 
 , то «негласно» подразумевается пропорция
, то «негласно» подразумевается пропорция  .
. . Найти:
. Найти: в отношении
в отношении 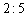 ;
; , делящую отрезок
, делящую отрезок  .
. принадлежит отрезку
принадлежит отрезку  . Известно, что отрезок
. Известно, что отрезок  в два раза длиннее отрезка
в два раза длиннее отрезка  . Найти точку
. Найти точку  , если
, если  .
. , считая от вершины
, считая от вершины  , то есть, справедлива пропорция:
, то есть, справедлива пропорция:  . По формулам деления отрезка в данном отношении:
. По формулам деления отрезка в данном отношении:
 , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
, но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями: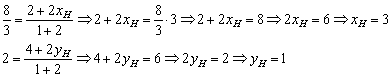

 и, пользуясь формулами в прямом порядке, убедиться, что при соотношении
и, пользуясь формулами в прямом порядке, убедиться, что при соотношении  . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
. И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения: . Отрезок
. Отрезок  .
. , то координаты точки
, то координаты точки  , которая делит отрезок
, которая делит отрезок  .
. . Найти координаты точки
. Найти координаты точки  .
. . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость – пропорцию в условии рациональнее было записать так:
. Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость – пропорцию в условии рациональнее было записать так: 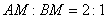 .
.

 пойдёт, но вариант с неправильными дробями более стандартен.
пойдёт, но вариант с неправильными дробями более стандартен. . Найти координаты точки
. Найти координаты точки  в отношении
в отношении  .
.
 . И общие формулы
. И общие формулы 

 , то координаты его середины
, то координаты его середины 
 . Найти точку пересечения его диагоналей.
. Найти точку пересечения его диагоналей. делятся пополам, поэтому задачу можно решить двумя способами.
делятся пополам, поэтому задачу можно решить двумя способами.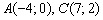 . По формулам деления отрезка пополам найдём середину диагонали
. По формулам деления отрезка пополам найдём середину диагонали 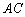 :
:

 . По формулам деления отрезка пополам найдём середину диагонали
. По формулам деления отрезка пополам найдём середину диагонали  :
:
 . Найти середину
. Найти середину  отрезка
отрезка  .
.
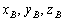 . И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:
. И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:
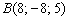
 и находим его середину.
и находим его середину. . Используем формулы деления отрезка в данном отношении:
. Используем формулы деления отрезка в данном отношении: 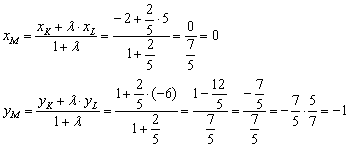

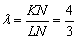 . Используем формулы деления отрезка в данном отношении:
. Используем формулы деления отрезка в данном отношении: 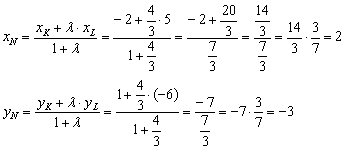
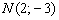
 .
.


 .
. 

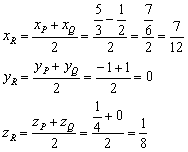

 называется уравнением прямой с угловым коэффициентом
называется уравнением прямой с угловым коэффициентом  . Например, если прямая задана уравнением
. Например, если прямая задана уравнением  , то её угловой коэффициент:
, то её угловой коэффициент:  . Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:
. Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:
 и данной прямой:
и данной прямой:  , причём угол
, причём угол  «откручивается» против часовой стрелки.
«откручивается» против часовой стрелки. . Согласно вышесказанному:
. Согласно вышесказанному:  (угол «альфа» обозначен зелёной дугой). Для «синей» прямой
(угол «альфа» обозначен зелёной дугой). Для «синей» прямой  с угловым коэффициентом
с угловым коэффициентом  справедливо равенство
справедливо равенство  (угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс.
(угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс.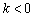 , то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.
, то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.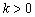 , то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.
, то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже. , то уравнение
, то уравнение  , и соответствующая прямая параллельна оси
, и соответствующая прямая параллельна оси 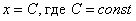 , параллельных оси
, параллельных оси  (на чертеже нет примера, кроме самой оси
(на чертеже нет примера, кроме самой оси  , а тангенса угла 90 градусов не существует.
, а тангенса угла 90 градусов не существует. . Здесь
. Здесь  , поэтому прямая
, поэтому прямая  имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов. .
. справедливо неравенство
справедливо неравенство  , таким образом, прямая
, таким образом, прямая  более полога.
более полога. весьма крутА и идёт снизу вверх, а прямая
весьма крутА и идёт снизу вверх, а прямая  – очень полога, близко прижата к оси
– очень полога, близко прижата к оси  и идёт сверху вниз.
и идёт сверху вниз. . Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через
. Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через 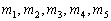 .
.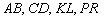 и т.д. Обозначение
и т.д. Обозначение  принадлежат прямой
принадлежат прямой  , принадлежащая некоторой прямой, и угловой коэффициент
, принадлежащая некоторой прямой, и угловой коэффициент 
 , если известно, что точка
, если известно, что точка  принадлежит данной прямой.
принадлежит данной прямой.


 , и точка
, и точка  принадлежит данной прямой.
принадлежит данной прямой.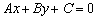 , где
, где 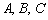 – некоторые числа. При этом коэффициенты
– некоторые числа. При этом коэффициенты  одновременно не равны нулю, так как уравнение теряет смысл.
одновременно не равны нулю, так как уравнение теряет смысл.


 .
.
 равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.
равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.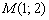 и направляющему вектору
и направляющему вектору 





 и без проблем подобрать ещё одну точку для построения прямой.
и без проблем подобрать ещё одну точку для построения прямой. . Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой
. Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой  :
:


 или любой другой коллинеарный вектор.
или любой другой коллинеарный вектор. является направляющим вектором данной прямой.
является направляющим вектором данной прямой.
 задаёт прямую, которая параллельна оси
задаёт прямую, которая параллельна оси  удобно разделить на –2, получая в точности базисный вектор
удобно разделить на –2, получая в точности базисный вектор 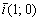 в качестве направляющего вектора. Логично.
в качестве направляющего вектора. Логично. задаёт прямую, параллельную оси
задаёт прямую, параллельную оси  , и, разделив координаты вектора
, и, разделив координаты вектора 


