

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Аналитическая геометрия
Векторы. Действия с векторами.
Координаты вектора. Простейшие задачи с векторами.
Что означает прилагательное «аналитическая»? Аналитическое решение предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решений практически всех задач аналитической геометрии заключается в применении формул.
Понятие вектора. Свободный вектор
Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
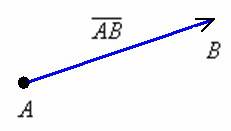
В данном случае началом отрезка является точка  , концом отрезка – точка
, концом отрезка – точка 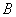 . Сам вектор обозначен через
. Сам вектор обозначен через  . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор
. Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор  , и это уже совершенно другой вектор.
, и это уже совершенно другой вектор.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором 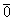 . У такого вектора конец и начало совпадают.
. У такого вектора конец и начало совпадают.
!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.
Способызаписи векторов:
1) Векторы можно записать двумя большими латинскими буквами:
 и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
2) Векторы также записывают маленькими латинскими буквами:
 В частности, наш вектор
В частности, наш вектор  можно для краткости пере обозначить маленькой латинской буквой
можно для краткости пере обозначить маленькой латинской буквой  .
.
Длиной или модулем ненулевого вектора  называется длина отрезка
называется длина отрезка  . Длина нулевого вектора
. Длина нулевого вектора 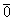 равна нулю. Логично.
равна нулю. Логично.
Длина вектора обозначается знаком модуля:  ,
, 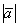
|
|
Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.
То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.
Если совсем просто – вектор можно отложить от любой точки:

Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте вектор произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ.
Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.
Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения вектора имеет значение.
Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.
Как найти длину вектора?
Если дан вектор плоскости 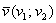 , то его длина вычисляется по формуле
, то его длина вычисляется по формуле 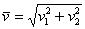 .
.
Если дан вектор пространства  , то его длина вычисляется по формуле
, то его длина вычисляется по формуле  .
.
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
Пример 5
Даны точки  и
и  . Найти длину вектора
. Найти длину вектора  .
.
Я взял те же точки, что и в Примере 3.
Решение: Сначала найдём вектор  :
:
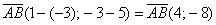
По формуле 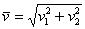 вычислим длину вектора:
вычислим длину вектора:

Ответ: 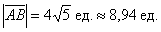
Выполним чертеж к задаче:

В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.
|
|
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка  равна длине вектора
равна длине вектора  . Так же очевидно, что длина вектора
. Так же очевидно, что длина вектора  будет такой же. По итогу:
будет такой же. По итогу: 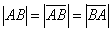
Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки  и
и  . Найти длину отрезка
. Найти длину отрезка  .
.
Вместо применения формулы  , поступаем так:
, поступаем так:
1) Находим вектор 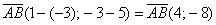 .
.
2) А теперь ссылаемся на то, что длина отрезка  равна длине вектора
равна длине вектора  :
:

Этот способ широко практикуется в ходе решений задач аналитической геометрии.
Вышесказанное справедливо и для пространственного случая
Для тренировки:
Пример 6
а) Даны точки  и
и 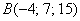 . Найти длину вектора
. Найти длину вектора  .
.
б) Даны векторы  ,
,  ,
,  и
и  . Найти их длины.
. Найти их длины.
Решения и ответы в конце.
Угол между векторами
Продолжаем выжимать полезные вещи из скалярного произведения. Снова посмотрим на нашу формулу  . По правилу пропорции сбросим длины векторов в знаменатель левой части:
. По правилу пропорции сбросим длины векторов в знаменатель левой части:
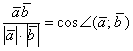
А части поменяем местами:

В чём смысл данной формулы? Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.
Скалярное произведение 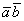 – это число? Число. Длины векторов
– это число? Число. Длины векторов  – числа? Числа. Значит, дробь
– числа? Числа. Значит, дробь  тоже является некоторым числом
тоже является некоторым числом  . А если известен косинус угла:
. А если известен косинус угла: 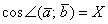 , то с помощью обратной функции легко найти и сам угол:
, то с помощью обратной функции легко найти и сам угол: 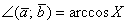 .
.
Пример 7
Найти угол между векторами  и
и  , если известно, что
, если известно, что  .
.
Решение: Используем формулу:

На заключительном этапе вычислений использован технический приём – устранение иррациональности в знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на  .
.
Итак, если  , то:
, то:

Ответ: 
Опять, не забываем указывать размерность – радианы и градусы. Теперь вы сможете самостоятельно справиться с более сложным заданием:
Пример 7*
Даны  – длины векторов
– длины векторов  ,
,  и угол между ними
и угол между ними  . Найти угол между векторами
. Найти угол между векторами  ,
,  .
.
Задание даже не столько сложное, сколько многоходовое.
Разберём алгоритм решения:
1) По условию требуется найти угол между векторами  и
и 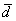 , поэтому нужно использовать формулу
, поэтому нужно использовать формулу  .
.
2) Находим скалярное произведение  (см. Примеры №№3,4).
(см. Примеры №№3,4).
3) Находим длину вектора  и длину вектора
и длину вектора 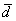 (см. Примеры №№5,6).
(см. Примеры №№5,6).
4) Концовка решения совпадает с Примером №7 – нам известно число  , а значит, легко найти и сам угол:
, а значит, легко найти и сам угол: 
Краткое решение и ответ в конце.
Скалярное произведение векторов,
заданных координатами в ортонормированном базисе
|
|
Прежде чем продолжать дальше, скажу, что все рассмотренные выше утверждения, теоремы и задачи (первого раздела данной статьи) справедливы как для плоскости, так и для пространства.
Второе важное замечание касается базиса. В данном разделе рассматриваются только ортонормированные базисы плоскости и пространства.
Повествование опять пойдёт параллельно – и для векторов плоскости и для пространственных векторов.
Скалярное произведение в координатах
Скалярное произведение векторов 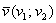 и
и  , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 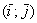 , выражается формулой
, выражается формулой 
Скалярное произведение векторов  , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 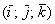 , выражается формулой
, выражается формулой 
То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.
Пример 8
Найти скалярное произведение векторов:
а)  и
и 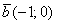
б)  и
и  , если даны точки
, если даны точки 
Решение:
а) Здесь даны векторы плоскости. По формуле  :
:

К слову: скалярное произведение получилось отрицательным, значит, угол между данными векторами является тупым. Пытливые умы могут отложить на плоскости векторы 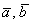 от одной точки, и убедиться, что это действительно так.
от одной точки, и убедиться, что это действительно так.
б) А тут речь идёт о точках и векторах пространства. Сначала найдём векторы:

Надеюсь, эта простейшая задача у вас уже отработана.
По формуле  вычислим скалярное произведение:
вычислим скалярное произведение:

К слову: скалярное произведение положительно, значит, угол между пространственными векторами 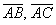 является острым.
является острым.
Ответ: 
Проверка векторов на ортогональность с помощью скалярного произведения
Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю: векторы  и
и  ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда  . В координатах данный факт запишется следующим образом:
. В координатах данный факт запишется следующим образом:
 (для векторов плоскости);
(для векторов плоскости);
 (для векторов пространства).
(для векторов пространства).
Пример 9
а) Проверить ортогональность векторов: 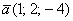 и
и 
б) Выяснить, будут ли перпендикулярными отрезки  и
и 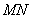 , если
, если 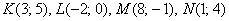
Решение:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение:
 , следовательно,
, следовательно, 
б) Здесь речь идёт об обычных отрезках плоскости (в чём сходство и различия вектора и отрезка, я очень подробно разъяснил на первом уроке). Речь идёт об обычных отрезках, а задача всё равно решается через векторы. Найдём векторы:

|
|
Вычислим их скалярное произведение:
 , значит, отрезки
, значит, отрезки  и
и 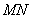 не перпендикулярны.
не перпендикулярны.
Обратите внимание на два существенных момента:
– В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
– В окончательном выводе «между строк» подразумевается: «если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными». Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках: «значит, отрезки  и
и 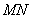 не перпендикулярны».
не перпендикулярны».
Ответ: а)  , б) отрезки
, б) отрезки  не перпендикулярны.
не перпендикулярны.
Пример 10
Даны четыре точки пространства  . Выяснить будут ли перпендикулярными следующие прямые:
. Выяснить будут ли перпендикулярными следующие прямые:
а)  ;
;
б)  .
.
Это задача для самостоятельного решения. В условии требуется проверить перпендикулярность прямых. А решается задача снова через векторы по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно – если удастся доказать перпендикулярность векторов, то из этого автоматически будет следовать перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых.
Полное решение и ответ в конце.
Пример 11
При каком значении  векторы
векторы  будут ортогональны?
будут ортогональны?
Решение: По условию требуется найти такое значение параметра  , чтобы данные векторы были ортогональны. Два вектора пространства
, чтобы данные векторы были ортогональны. Два вектора пространства  ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 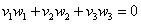 .
.
Дело за малым, составим уравнение:

Раскрываем скобки и приводим подобные слагаемые:

Решаем простейшее линейное уравнение:

Ответ: при 
В рассмотренной задаче легко выполнить проверку, в исходные векторы  подставляем полученное значение параметра
подставляем полученное значение параметра  :
:

И находим скалярное произведение:
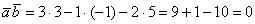 – да, действительно, при
– да, действительно, при  векторы
векторы 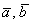 ортогональны, что и требовалось проверить.
ортогональны, что и требовалось проверить.
Пример 12
При каком значении  скалярное произведение векторов
скалярное произведение векторов  будет равно –2?
будет равно –2?
Это простенький пример с векторами плоскости. Для самостоятельного решения.
Немного усложним задачу:
Скалярное произведение в координатах, если векторы заданы суммами векторов
Пример 13
Найти скалярное произведение векторов  , если
, если 
Решение: напрашивается трафаретный путь предыдущего раздела, где мы раскрывали скобки:  . Но зачем? Есть более лаконичное решение:
. Но зачем? Есть более лаконичное решение:
Найдём вектор  :
:

Найдём вектор 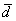 :
:
 .
.
Вычислим скалярное произведение:

Ответ: 
Пример 14
Найти скалярное произведение векторов  и
и  , если
, если 
Это пример для самостоятельного решения. Здесь можно использовать ассоциативность операции, то есть не считать  , а сразу вынести тройку за пределы скалярного произведения и домножить на неё в последнюю очередь. Решение и ответ в конце урока.
, а сразу вынести тройку за пределы скалярного произведения и домножить на неё в последнюю очередь. Решение и ответ в конце урока.
|
|
В заключение параграфа провокационный пример на вычисление длины вектора:
Пример 15
Найти длины векторов  , если
, если 
Решение: снова напрашивается способ предыдущего раздела:  , но существует и другая дорога:
, но существует и другая дорога:
Найдём вектор  :
:
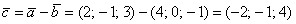
И его длину по тривиальной формуле  :
:

При вычислении длины вектора  :
:
 можно воспользоваться очевидным свойством длины вектора? Что можно сказать о длине вектора
можно воспользоваться очевидным свойством длины вектора? Что можно сказать о длине вектора  ? Данный вектор длиннее вектора
? Данный вектор длиннее вектора  в 5 раз. Направление противоположно, но это не играет роли, ведь разговор о длине. Очевидно, что длина вектора
в 5 раз. Направление противоположно, но это не играет роли, ведь разговор о длине. Очевидно, что длина вектора  равна произведению модуля числа
равна произведению модуля числа  на длину вектора
на длину вектора  :
:
 – знак модуля «съедает» возможный минус числа
– знак модуля «съедает» возможный минус числа  .
.
Таким образом:

Ответ: 
Формула косинуса угла между векторами, которые заданы координатами
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами  выразить через координаты векторов
выразить через координаты векторов  :
:
Косинус угла между векторами плоскости 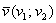 и
и  , заданными в ортонормированном базисе
, заданными в ортонормированном базисе 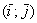 , выражается формулой:
, выражается формулой:
 .
.
Косинус угла между векторами пространства  , заданными в ортонормированном базисе
, заданными в ортонормированном базисе 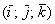 , выражается формулой:
, выражается формулой:
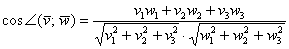
Пример 16
Даны три вершины треугольника  . Найти
. Найти  (угол при вершине
(угол при вершине  ).
).
Решение: По условию чертёж выполнять не требуется, но всё-таки:

Требуемый угол  помечен зелёной дугой. Сразу вспоминаем школьное обозначение угла:
помечен зелёной дугой. Сразу вспоминаем школьное обозначение угла:  – особое внимание на среднюю букву
– особое внимание на среднюю букву 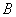 – это и есть нужная нам вершина угла. Для краткости можно было также записать просто
– это и есть нужная нам вершина угла. Для краткости можно было также записать просто 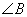 .
.
Из чертежа совершенно очевидно, что угол  треугольника совпадает с углом между векторами
треугольника совпадает с углом между векторами  и
и  , иными словами:
, иными словами:  .
.
Проведённый анализ желательно научиться выполнять мысленно.
Найдём векторы:

Вычислим скалярное произведение:

И длины векторов:

Косинус угла:

«одной строкой»:
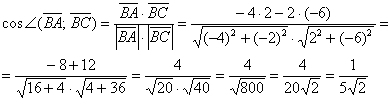
Вот и пример «плохого» значения косинуса. Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:

Ответ: 
В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем указать точный ответ:  и приближенное значение угла:
и приближенное значение угла:  , найденное с помощью калькулятора.
, найденное с помощью калькулятора.
Те, кто получил удовольствие от процесса, могут вычислить углы  , и убедиться в справедливости канонического равенства
, и убедиться в справедливости канонического равенства 
Пример 17
В пространстве задан треугольник координатами своих вершин  . Найти угол между сторонами
. Найти угол между сторонами  и
и 
Это пример для самостоятельного решения. Полное решение и ответ в конце
Проекция вектора на вектор. Проекция вектора на координатные оси.
Направляющие косинусы вектора
Рассмотрим векторы  и
и 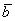 :
:

Спроецируем вектор  на вектор
на вектор 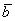 , для этого из начала и конца вектора
, для этого из начала и конца вектора  опустим перпендикуляры на вектор
опустим перпендикуляры на вектор 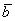 (зелёные пунктирные линии). Представьте, что на вектор
(зелёные пунктирные линии). Представьте, что на вектор 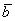 перпендикулярно падают лучи света. Тогда отрезок
перпендикулярно падают лучи света. Тогда отрезок  (красная линия) будет «тенью» вектора
(красная линия) будет «тенью» вектора  . В данном случае проекцией вектора
. В данном случае проекцией вектора  на вектор
на вектор 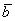 является ДЛИНА отрезка
является ДЛИНА отрезка  . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Данное ЧИСЛО обозначается следующим образом:  , «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.
, «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись  читается так: «проекция вектора «а» на вектор «б»».
читается так: «проекция вектора «а» на вектор «б»».
Что произойдёт, если вектор «б» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «б». И вектор «а» будет проецироваться уже на направление вектора «б», попросту – на прямую, содержащую вектор «б». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «б».
Если угол между векторами 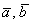 острый (как на рисунке), то
острый (как на рисунке), то 
Если векторы 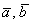 ортогональны, то
ортогональны, то  (проекцией является точка, размеры которой считаются нулевыми).
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами 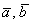 тупой (на рисунке мысленно переставьте стрелочку вектора
тупой (на рисунке мысленно переставьте стрелочку вектора  ), то
), то  (та же длина, но взятая со знаком минус).
(та же длина, но взятая со знаком минус).
Отложим данные векторы от одной точки:

Очевидно, что при перемещении вектора его проекция не меняется
Вспомним школу. Рассмотрим прямоугольный треугольник. Косинусом острого угла называется отношение прилежащего катета к гипотенузе. В данном случае:

С другой стороны, у нас уже получена формула косинуса угла между векторами:

Таким образом:

Сокращаем знаменатели обеих частей на  и получаем формулу для вычисления проекции:
и получаем формулу для вычисления проекции:

Формула выведена, распишем её в координатах:
Если векторы плоскости 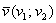 и
и  , заданы в ортонормированном базисе
, заданы в ортонормированном базисе 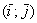 , то проекция вектора
, то проекция вектора  на вектор
на вектор  выражается формулой:
выражается формулой:
 .
.
Если векторы пространства  , заданы в ортонормированном базисе
, заданы в ортонормированном базисе 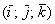 , то проекция вектора
, то проекция вектора  на вектор
на вектор  выражается формулой:
выражается формулой:

Пример 18
Найти проекцию вектора  на вектор
на вектор 
Решение в одну строчку:

Ответ: 
Проекция – это ДЛИНА, поэтому обязательно указываем размерность. Длина, конечно, своеобразная, в случае тупизны угла между векторами к ней добавляется знак «минус».
В задачах приходится находить не только проекцию вектора на вектор, но и проекцию отрезка на отрезок, отрезка на прямую и т.д. Но, так или иначе, в решении используются векторы!
Пример 19
Треугольник задан своими вершинами  . Найти:
. Найти:
а) проекцию стороны  на сторону
на сторону  ;
;
б) проекцию стороны  на сторону
на сторону  .
.
Это задача для самостоятельного решения. Решение и ответ в конце.
Выясним геометрический смысл координат векторов в ортонормированном базисе:
Проекция вектора на координатные оси.
Направляющие косинусы вектора
Рассмотрим вектор плоскости  , заданный своими координатами в ортонормированном базисе
, заданный своими координатами в ортонормированном базисе 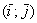 . Для удобства я отложу его от начала координат:
. Для удобства я отложу его от начала координат:

Проекцией вектора  на координатную ось
на координатную ось  является в точности его первая координата:
является в точности его первая координата: 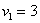 (красная черта). Обозначим через
(красная черта). Обозначим через  угол между вектором
угол между вектором  и координатным вектором
и координатным вектором  :
:  (красная дуга). Тогда:
(красная дуга). Тогда:
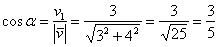 (определение косинуса в прямоугольном треугольнике недавно упоминалось).
(определение косинуса в прямоугольном треугольнике недавно упоминалось).
Аналогично со второй координатой: проекцией вектора  на координатную ось
на координатную ось  является его вторая координата:
является его вторая координата:  (малиновая черта). Обозначим через
(малиновая черта). Обозначим через  угол между вектором
угол между вектором  и координатным вектором
и координатным вектором  :
:  (двойная малиновая дуга). Тогда:
(двойная малиновая дуга). Тогда:

Косинусы  называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство
называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство  . Проверим его справедливость для рассматриваемого вектора:
. Проверим его справедливость для рассматриваемого вектора:
 , что и требовалось проверить.
, что и требовалось проверить.
Заметьте, что приведённые выше выкладки не изменятся, если вектор  отложить от любой другой точки плоскости.
отложить от любой другой точки плоскости.
Итак, координаты вектора в ортонормированном базисе – это его проекции на направления соответствующих координатных векторов (координатные оси).
Направляющие косинусы ненулевого вектора 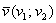 , заданного в ортонормированном базисе
, заданного в ортонормированном базисе 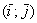 , выражаются формулами
, выражаются формулами  , а сами координаты вектора можно выразить через его длину и данные косинусы:
, а сами координаты вектора можно выразить через его длину и данные косинусы:  , то есть:
, то есть:  .
.
Кроме того, вектор с координатами из соответствующих направляющих косинусов:
– коллинеарен исходному вектору «в»;
– его длина равна единице (так называемый единичный вектор).
С пространственными векторами, заданными в ортонормированном базисе 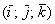 , разборки точно такие же. Рассмотрим произвольный ненулевой вектор
, разборки точно такие же. Рассмотрим произвольный ненулевой вектор  . Его координаты представляют собой проекции вектора на оси
. Его координаты представляют собой проекции вектора на оси  соответственно. Обозначим углы данного вектора с ортами через:
соответственно. Обозначим углы данного вектора с ортами через:  . Тогда направляющие косинусы вектора выражаются формулами:
. Тогда направляющие косинусы вектора выражаются формулами:  , и справедливым является равенство
, и справедливым является равенство  .
.
В практических задачах чаще всего требуется найти направляющие косинусы вектора, заключительный пример урока:
Пример 20
Найти направляющие косинусы векторов:
а)  , проверить, что
, проверить, что  ;
;
б)  , проверить, что
, проверить, что  .
.
Простая задача для самостоятельного решения. Фактически, она состоит в том, чтобы найти длину векторов и составить эти самые направляющие косинусы. Однако не забывайте, что вместе с направляющими косинусами нам автоматически становятся известными единичные векторы, которые коллинеарны векторам «а» и «б».
Пример 2: Решение:
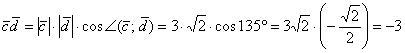
Ответ: 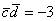
Пример 4: Решение:

Ответ: 
Пример 6: Решение:

Ответ: 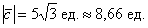
Пример 7*: Решение: Используем формулу  .
.
Найдём скалярное произведение:

Найдём длину вектора  :
:

Найдём длину вектора 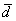 :
:

Таким образом:

Ответ: 
Пример 10: Решение:
а) Найдем векторы:

Вычислим скалярное произведение:
 , значит, прямые
, значит, прямые  не перпендикулярны.
не перпендикулярны.
б) Найдем векторы:
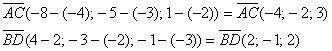
Вычислим скалярное произведение:
 , значит, прямые
, значит, прямые  перпендикулярны.
перпендикулярны.
Ответ: а) прямые  не перпендикулярны, б)
не перпендикулярны, б) 
Пример 12: Решение: Составим и решим уравнение:

Ответ: при 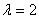
Пример 14: Решение:

Ответ: 
Пример 17: Решение: Найдем векторы 
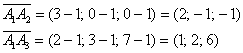
Вычислим косинус угла:
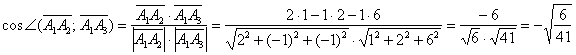
Угол: 
Ответ: 
Пример 19: Решение: Найдём векторы:


Ответ: 
Пример 20: Решение:
а) Найдём длину вектора:  .
.
Направляющие косинусы:  .
.
Проверка:  , что и требовалось проверить.
, что и требовалось проверить.
б) Найдём длину вектора:  .
.
Направляющие косинусы:
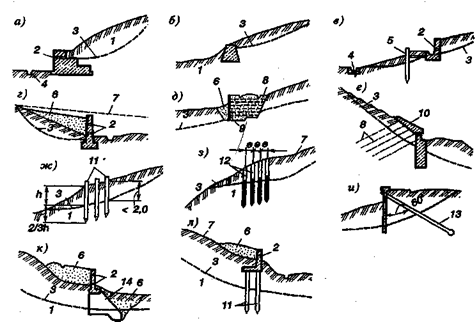
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
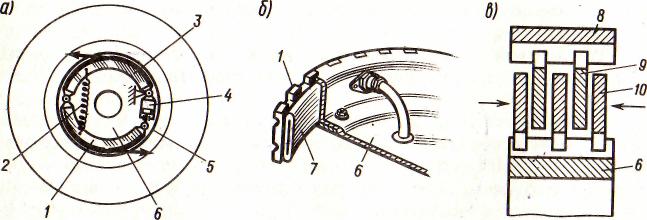
Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
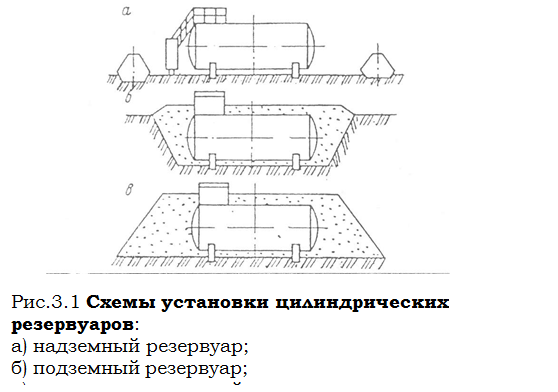
История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!