МАТЕМАТИКА
Программа, методические указания и задания к выполнению контрольной работы для учащихся заочной формы получения образования специальности 2-27 01 01 «Экономика и организация производства»
Содержание
| Введение
|
|
| 1. Тематический план
|
|
| 2. Содержание дисциплины и методические рекомендации по ее
изучению
|
|
| 3. Общие указания по выполнению контрольной работы
|
|
| 4. Варианты заданий для домашней контрольной работы
|
|
| 5. Задания домашней контрольной работы
|
|
| Приложение 1 Контрольные вопросы по курсу изучения дисциплины
"Математика"
|
|
| Приложение 2 Формулы тригонометрии
|
|
| Литература
|
|
Введение
Современное состояние развития общества характеризуется математизацией и информатизацией всего научного знания. Обладая огромным эвристическим потенциалом, математика облегчает стратегические оценки широкого спектра задач, обеспечивает экономическое развитие общества.
Важность математического образования обусловлена еще и тем, что математика – неотъемлемая и существенная часть общечеловеческой культуры. Поэтому следует подчеркнуть большую роль математического образования при формировании общей культуры человека.
Основными задачами математического образования учащихся ССО являются:
· формирование математической компетентности учащихся в контексте будущей профессиональной деятельности и для продолжения образования;
· обучение учащихся навыкам использования основных общенаучных методов познания с целью их последующего применения в профессиональной деятельности для анализа и исследования реальных процессов и явлений;
· формирование представлений о методологическом значении и роли математики в научно-техническом прогрессе, о культурологической сущности математики.
Дисциплина "Математика" изучается самостоятельно по рекомендуемой литературе. Теоретическое изучение дисциплины расширяется и углубляется выполнением практических заданий во время сессии и одной домашней контрольной работы, которая содержит 8 заданий и выполняется по вариантам.
Изучать программный материал рекомендуется не только по предлагаемой литературе, но и используя другие учебники и справочники.
После усвоения темы следует устно ответить на вопросы для самопроверки.
1. Примерный тематический план
|
Тема
| Количество часов
|
|
Всего
| На самостоят.изучение
| Обзор-ные лекции
| В т.ч. практ. занятия
|
| 1. Введение в курс математики
|
|
|
|
|
| 2. Матрицы и определители. Системы линейных алгебраических уравнений
|
|
|
|
|
| 3. Функция. Последовательность
|
|
|
|
|
| 4. Предел последовательности и предел функции. Непрерывность функции
|
|
|
|
|
| 5. Дифференциальное исчисление функций одной и многих переменных
|
|
|
|
|
| 6. Неопределенный интеграл. Определенный интеграл
|
|
|
|
|
| 7. Дифференциальные уравнения
|
|
|
|
|
| 8. Комбинаторика, теория графов, теория вероятностей
|
|
|
|
|
| 9. Профессионально значимые темы
|
|
|
|
|
| Всего:
|
|
|
|
|
2. Содержание дисциплины и методические рекомендации по ее изучению
Тема 1. Введение в курс математики
Содержание программы
1.1. Математика как составная часть мировой культуры и ее роль в научно-техническом прогрессе. Значение математического образования для подготовки специалистов со средним специальным образованием.
1.2. Высказывания. Логические операции над высказываниями. Типы теорем. Система и совокупность утверждений.
1.3. Знак конечной суммы элементов 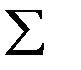 .Факториал.
.Факториал.
1.4. Множества и операции над множествами. Числовые множества N, Z, Q, I, R.
1.5. Расширение понятия числа. Понятие комплексного числа, арифметические действия над комплексными числами.
1.6. Формулы сокращенного умножения.
1.7. Многочлены. Корни многочлена. Действия над многочленами. Разложение многочленов на множители.
Содержание темы
Введение
Применение математических методов в экономике теперь уже вышло из стадии только теоретических рассуждений, математические методы все больше и больше внедряются в практику планирования и анализа деятельности предприятий.
А.Г.Лукашенко было сказано: «Внимание экономистов должно быть направлено на изыскания путей наиболее эффективного использования в народном хозяйстве материальных и трудовых ресурсов, наилучших методов планирования и организации промышленного и сельскохозяйственного производства».
Многочлены
Выражение вида 
где  называется многочленом n-й степени от одной переменной х, записанным в стандартном виде.
называется многочленом n-й степени от одной переменной х, записанным в стандартном виде.
Числа  называются коэффициентами данного многочлена,
называются коэффициентами данного многочлена, 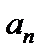 – старшим коэффициентом,
– старшим коэффициентом,  – свободным членом. Число
– свободным членом. Число 
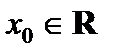 называется корнем многочлена
называется корнем многочлена  если
если 
Комплексные числа
Число вида z = a + bi, где а и b - действительные числа, i - мнимая единица, определяемая равенством i 2 = -1, называется комплексным числом. Любое комплексное число z = a + bi изображается точкой плоскости М (а, b) илирадиус-вектором  точки М. Обратно, любой точке М (а, b) плоскости соответствует комплексное число z = a + bi. Плоскость, точки которой отождествляются с комплексными числами, называют комплексной плоскостью, где ось Ох называется действительной осью, Оу – мнимой осью.
точки М. Обратно, любой точке М (а, b) плоскости соответствует комплексное число z = a + bi. Плоскость, точки которой отождествляются с комплексными числами, называют комплексной плоскостью, где ось Ох называется действительной осью, Оу – мнимой осью.
Im
b М
0 а Re
Пример 1.3. Изобразить комплексные числа на комплексной плоскости:
z1 = 2 + 3i, z2 = - i, z3 = 
Pешение
Чтобы изобразить z3 на комплексной плоскости, переведем его в алгебраическую форму:
z3 =  = 3(cos (π +
= 3(cos (π +  ) + isin (π +
) + isin (π +  )) = 3(- cos
)) = 3(- cos  - isin
- isin  ) =
) =
= 3(  )=
)=  .
.
Построим комплексную плоскость:
Im
3 z1
-2 0 1 2
z2 Re
z3
Выражение a + bi называют алгебраической формой комплексного числа. Число а называют действительной частью, число b - мнимой частью комплексного числа: а = Re z, b = Im z.
Два комплексных числа называют равными, если равны их соответствующие действительные и мнимые части. Комплексное число равно нулю, если равны нулю его действительная и мнимая часть.
Комплексные числа, отличающиеся знаком мнимой части, называются сопряженными и обозначаются z = a + bi и  = a - bi.
= a - bi.
Действия над комплексными числами в алгебраической форме:
1) чтобы сложить два комплексных числа, необходимо сложить соответственно их действительные и мнимые части:
(a + bi) + (c + di) = (a + c) + (b + d)i,
2) при вычитании одного комплексного числа из другого необходимо вычесть отдельно их действительные и мнимые части:
(a + bi) - (c + di) = (a - c) + (b - d)i,
3) умножение двух комплексных чисел выполняем по правилам алгебры и замены i2 его значением:
(a + bi)(c + di) = (aс - bd) + (bc + ad)i,
4) чтобы разделить два комплексных числа, нужно умножить числитель и знаменатель на число, сопряженное знаменателю:
 .
.
5) комплексное число возводят в степень по правилам алгебры, а также используя формулу бинома Ньютона, принимая во внимание, что
i2= -1
Пример 1.4 Вычислить (1 + i)8.
Решение
(1 + i)8 = ((1 + i)2)4 = (1 + 2i + i2)4 = (1 + 2i – 1)4 = (2i)4 = 16i4 = 16(i2)2 =
=16(-1)2 = 16
Ответ: 16.
Пример 1.5. Вычислить

Решение

Пример 1.6. Решите уравнение х2 – 2х + 5 = 0.
Решение
х2 – 2х + 5 = 0
D = - 16
x1 = 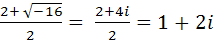 ,
,
x2 =  .
.
Ответ: x1 = 1 + 2i, x2 = 1 – 2i.
Пример 1.7. Решите уравнение 5х – 2у + хi + yi = 4 + 5i.
Решение
Следуя определению равенства двух комплексных чисел, выделим в левой и правой частях уравнения действительные и мнимые части и приравняем их.
(5х – 2у) + (х + у)i = 4 + 5i

Получили систему двух линейных уравнений с двумя неизвестными. Решая ее методом замены, найдем значения х и у.

Ответ: х = 2, у = 3.
Пример 1.8. Разложите на комплексные множители по формуле разности квадратов число 5.
Решение
5 = 4 + 1 = 4 – (- 1) = 4 – i2 = (2 – i)(2 + i).
Ответ: (2 – i)(2 + i).
Решение
Если число 1 + i  возвести в 9-ую степень по правилам действия над комплексными числами в алгебраической форме, то мы не достигнем необходимого результата. В данном случае сначала комплексное число представим в тригонометрической форме, а затем уже возведем в степень. Найдем модель и аргумент комплексного числа z = 1 + i
возвести в 9-ую степень по правилам действия над комплексными числами в алгебраической форме, то мы не достигнем необходимого результата. В данном случае сначала комплексное число представим в тригонометрической форме, а затем уже возведем в степень. Найдем модель и аргумент комплексного числа z = 1 + i  .
.
r =  = 2,
= 2,
Т. к. a > 0, b > 0, то φ =  =
= 
 2(cos
2(cos  )
) 
z9 = 29 (cos  + isin
+ isin  ) = 512 (cos 3π + isin 3π) = 512 (- 1 + i . 0) = - 512
) = 512 (cos 3π + isin 3π) = 512 (- 1 + i . 0) = - 512
Ответ: - 512
Показательная форма комплексного числа имеет вид
z = re iφ
где e iφ = сos φ + sin φ – формула Эйлера,
r =  - модуль комплексного числа,
- модуль комплексного числа,
φ = arg z – аргумент комплексного числа, вычисление которого смотрите выше.
Действия над комплексными числами в показательной форме:
1) z1z2 = r1r2  ,
,
2)  =
=  ,
,
3) z n = r n e inφ
Контрольные вопросы
1. Какую роль играет математика в развитии мировой культуры?
2. Что называется высказыванием?
3. Назовите логические операции над высказываниями.
4. Что определяет знак  ?
?
5. Что называется факториалом числа?
6. Дайте определения множества и операций над множествами.
7. Какие числовые множества вы знаете?
8. Что называется многочленом?
9. Назовите действия над многочленами.
10. Что называется корнем многочлена?
11. Как разложить многочлен на множители?
12. Что называют комплексным числом?
13. Как определяется мнимая единица?
14. Какова алгебраическая форма комплексного числа?
15. Как изображается геометрически комплексное число?
16. Что представляет собой комплексная плоскость?
17. Что называют действительной частью комплексного числа?
18. Что называют мнимой частью комплексного числа?
19. Какие комплексные числа называют сопряженными?
20. Как определяется равенство комплексных чисел?
21. Что следует из равенства a + bi = 0?
22. Каковы правила сложения и вычитания комплексных чисел?
23. Как найти частное двух комплексных чисел?
24. Что называется модулем комплексного числа, как его найти?
25. Что называют аргументом комплексного числа, как его найти?
26. Что представляет собой тригонометрическая форма комплексного числа?
27. Какова формула произведения двух комплексных чисел?
28. Какова формула частного двух комплексных чисел?
29. Что представляет собой формула Муавра?
Содержание программы
1.1. Понятие матрицы с числовыми элементами, виды матриц. Линейные операции над матрицами.
1.2. Транспонирование и умножение матриц. Степень матрицы с натуральным показателем.
1.3. Элементарные преобразования матриц, эквивалентные матрицы. Сведение матрицы к треугольной и трапециевидной формам.
1.4. Определители 2-ги и 3-го порядков, их свойства, способы вычисления.
1.5. Понятие систем линейных алгебраических уравнений с тремя неизвестными.
1.6. Решение систем линейных алгебраических уравнений с тремя неизвестными методом Крамера.
1.7. Решение систем линейных алгебраических уравнений с тремя неизвестными методом Гаусса.
Содержание темы
Матрицы и операции над ними
Матрицей называется система т.п чисел, расположенных в прямоугольной таблице из т строк и п столбцов. Числа этой таблицы называются элементами матрицы. Обозначение матрицы:
 ;
;  ;
;  .
.
аij - элемент, принадлежащий i -ой строке и j -ому столбцу. Числа i и j называются индексами элемента. Матрицу, имеющую т строк и п столбцов, называют матрицей размеров т  п (читается т на п).
п (читается т на п).
Матрицу обозначают также одной заглавной буквой:
А =  .
.
Матрица называется квадратной, у которой число строк равно числу столбцов (т = п):

Порядком квадратной матрицы называется число её строк. Элементы а11, а22, ..., апп квадратной матрицы образуют её главную диагональ, элементы а1п, а2п-1, …, ап1 образуют побочную диагональ.
Треугольной называют матрицу, элементы которой, расположенные по одну сторону от главной диагонали, равны нулю.
 .
.
Две матрицы А и В называются равными (А=В), если они имеют одинаковое количество строк и одинаковое число столбцов и их соответствующие элементы равны.
Суммой (разностью) двух данных матриц одинаковой размерности является матрица той же размерности, элементы которой равны сумме (разности) соответствующих элементов данных матриц.
Чтобы умножить матрицу на число необходимо каждый элемент матрицы умножить на это число.
Произведением матрицы А размерности mxn на матрицу В размерности nxp называется матрица С размерности mxp элементы которой находятся по формуле сij=ai1·b1j+ ai2·b2j+…+ ain·bnj.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.
Элементарными преобразованиями матрицы называют следующие преобразования:
1) умножение строки (столбца) матрицы на число, отличное от нуля;
2) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
3) перестановка местами двух строк (столбцов).
Определитель матрицы
Определителем 2-го порядка называется число
а11а22 – а12а21 = 
Числа а11, а22, а12 , а 21 называются элементами определителя. Элементы а11, а22 образуют главную диагональ определителя, а12 , а21 - побочную.
Определитель обозначается ∆ или det.
Определителем 3-го порядка называется число
∆ = a11  - a12
- a12  + a13
+ a13 
Определитель III порядка можно вычислять методом Саррюса:
 = а11 . а22 . а33 + а12 . а23 . а31 + а13 . а21 . а32 – а13 . а22 . а31 –
= а11 . а22 . а33 + а12 . а23 . а31 + а13 . а21 . а32 – а13 . а22 . а31 –
– а12 . а21 . а33 – а11 . а23 . а32
Свойства определителей:
1. Величина определителя не изменится при замене строк столбцами с теми же номерами.
2. Величина определителя не изменится при сложении элементов какой-либо строки (столбца) с соответствующими элементами другой строки (столбца), умноженными на одно и то же число.
3. При перестановке двух строк (столбцов) определитель меняет знак.
4. Определитель равен нулю, если он содержит нулевую строку(столбец).
5. Определитель равен нулю, если элементы одной строки(столбца) пропорциональны соответствующим элементам другой строки (столбца).
6. Общий множитель всех элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.
Пример 2.1. Найти 2А-В+С, если

Решение
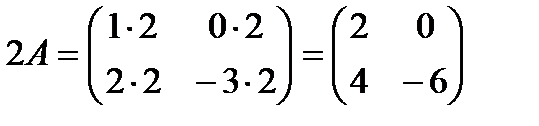


Пример 2.2. Найти произведение матриц  и
и  .
.
Решение
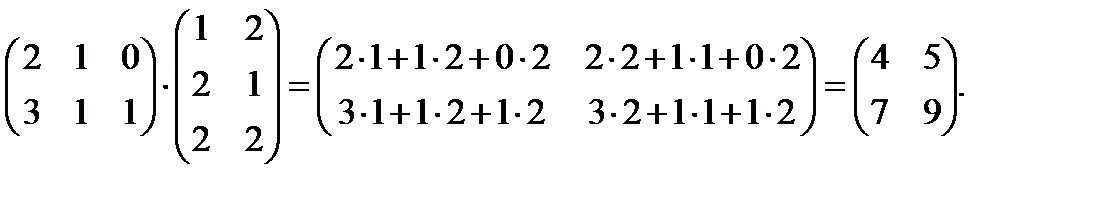
Пример 2.3. Вычислить определитель второго порядка 
Решение
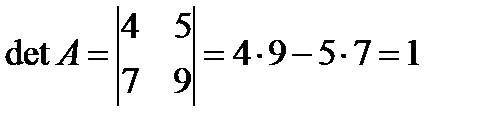
Пример 2.4. Вычислить определитель третьего порядка 
Решение
Найдем определитель по правилу Саррюса(треугольников)
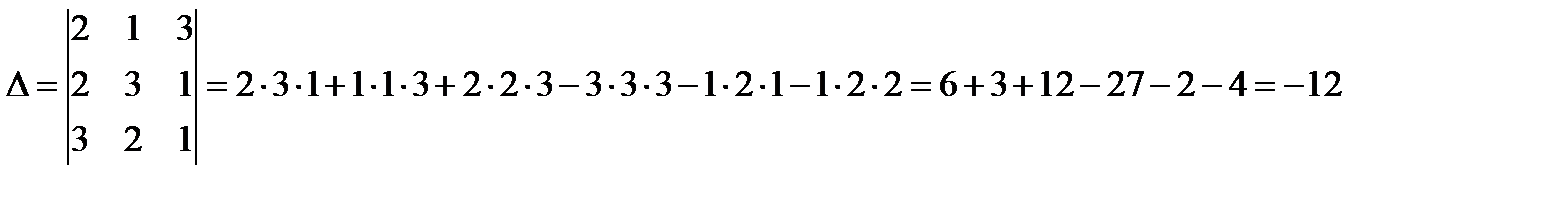
Решение
Вычислим определители:
 = 1 .
= 1 .  - 2 .
- 2 . 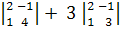 = 2.
= 2.
Т. к. определитель системы ∆ = 2 ≠ 0, то система имеет единственное решение.
 = 5 .
= 5 .  - 2 .
- 2 .  = 2,
= 2,
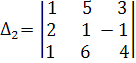 = 1 .
= 1 . 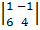 - 5 .
- 5 .  = - 2,
= - 2,
 = 1 .
= 1 .  - 2 .
- 2 .  = 4.
= 4.
По формуле Крамера:
 ,
,  .
.
Ответ: (1; - 1; 2)
Пусть требуется решить систему п линейных уравнений с п неизвестными

Наиболее распространенным методом решения системы линейных уравнений является алгоритм последовательного исключения неизвестных, который называется методом Гаусса. Согласно этому методу составляется соответствующая данной системе расширенная матрица и приводится к треугольному виду путем проведения преобразований над ее строками.

По полученной матрице составляется система линейных уравнений, решить которую не представляет трудности. Продемонстрируем данный метод на конкретных примерах.
Пример 2.6. Решить систему линейных уравнений методом Гаусса:

Решение
Запишем расширенную матрицу системы и преобразуем её:

К элементам второй строки прибавим соответствующие элементы первой строки, умноженные на (-2). К элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на (-3).

К элементам третьей строки прибавим соответствующие элементы второй строки, умноженные на (-2).

Оформим проведенные преобразования в виде:

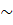


Полученной матрице соответствует система линейных уравнений:
 ⇔
⇔  ⇔
⇔ 
Ответ: (-1; 2; 3)
Пример 2.7. Решить систему линейных уравнений методом Гаусса:

Решение
Запишем расширенную матрицу системы и преобразуем её:


Запишем соответствующую полученной матрице систему. Зафиксировав х3 , выразим х2,х1:



Ответ: (
Контрольные вопросы
1. Что называется матрицей?
2. Какая матрица называется квадратной?
3. Как определяется порядок матрицы?
4. Какая матрица называется треугольной?
5. Какие элементарные преобразования можно производить над матрицами?
6. Назовите линейные операции над матрицами.
7. Что называется определителем первого прядка?
8. Что называется главной диагональю определителя?
9. Что называется побочной диагональю определителя?
10. Что представляет собой определитель второго порядка?
11. Как вычисляется определитель третьего порядка?
12. Какая система линейных уравнений называется совместной? Несовместной?
13. Какая линейная система называется невырожденной?
14. Что представляет собой определитель системы линейных уравнений?
15. Что представляют собой формулы Крамера для решения систем линейных уравнений?
16. В чём заключается метод Гаусса решения линейной системы?
Практическое занятие № 1 (2часа)
Содержание программы
3.1. Понятие функции, ее свойства, график. Сложная функция. Обратная функция.
3.2. Элементарные функции. Графики основных элементарных функций. Преобразования графиков.
3.3. Графический метод решения уравнений и систем двух уравнений с двумя неизвестными.
3.4. числовая последовательность. Виды последовательностей.
Содержание темы
Пусть X и Y некоторые числовые множества 

Если каждому  по некоторому правилу f ставится в соответствие единственный элемент
по некоторому правилу f ставится в соответствие единственный элемент 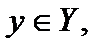 то говорят, что задана функция. Обозначается
то говорят, что задана функция. Обозначается  где х – аргумент или независимая переменная функции; у – значение функции или зависимая переменная.
где х – аргумент или независимая переменная функции; у – значение функции или зависимая переменная.
Множество Х значений независимой переменной называется областью определения функции и обозначается 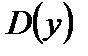 или
или 
Множество всех значений зависимой переменной Y называется множеством значений функции и обозначается  или
или 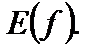
Частное значение функции  при заданном частном значении аргумента
при заданном частном значении аргумента 
 обозначается
обозначается 
Графиком функции  называется множество всех точек плоскости с координатами
называется множество всех точек плоскости с координатами  где
где 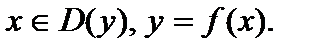
Свойства функции:
1. Четность и нечетность функции.
Функция  называется четной, если:
называется четной, если:
1)  – симметричное множество относительно
– симметричное множество относительно 
2) для любого  выполняется равенство
выполняется равенство 
Функция  называется нечетной, если:
называется нечетной, если:
1)  – симметричное множество относительно
– симметричное множество относительно 
2) для любого  выполняется равенство
выполняется равенство 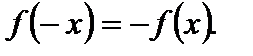
Если функция  является четной или нечетной, то говорят, что она обладает свойством четности.
является четной или нечетной, то говорят, что она обладает свойством четности.
График четной функции симметричен относительно оси  график нечетной – относительно начала координат.
график нечетной – относительно начала координат.
2. Периодичность функции.
Функция  с областью определения
с областью определения  называется периодической, если существует такое число
называется периодической, если существует такое число  что для любого значения
что для любого значения  выполняются условия:
выполняются условия:
1) 
2) 
Число Т называется периодом функции.
3. Монотонность функции.
Пусть х 1, х 2 – произвольные значения из области  функции
функции  такие, что
такие, что 
Если при данном условии выполняется:
 то функция называется возрастающей;
то функция называется возрастающей;
 – убывающей;
– убывающей;
 – неубывающей;
– неубывающей;
 – невозрастающей.
– невозрастающей.
4. Промежутки знакопостоянства функции. Нули функции.
Числовые промежутки, на которых функция сохраняет свой знак (т. е.  или
или  ), называются промежутками знакопостоянства.
), называются промежутками знакопостоянства.
Значения аргумента 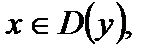 при которых функция
при которых функция 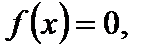 называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
Пример 3.1. Найти область определения функции

Решение 
 (3.1)
(3.1)
Найдем соответствующее  множество точек.
множество точек.
Неравенство  равносильно неравенству
равносильно неравенству

Решая его, получаем: 
Условие  означает, что
означает, что  т. е.
т. е. 
Приходим к заключению, что  Получаем
Получаем 
Таким образом, система (3.1) равносильна системе

Следовательно, 
Пример 3.2. Найти множество значений функции

Решение Найдем область определения функции 


Последнее условие выполняется только для  Вычисляем значение функции в этой точке:
Вычисляем значение функции в этой точке:  Следовательно,
Следовательно, 
Пример 3.3. Исследовать функцию на четность: 
Решение Замечаем, что функция  имеет
имеет  Следовательно, функция определена на симметричном множестве.
Следовательно, функция определена на симметричном множестве.
Рассмотрим ее значение для – х: 
Поскольку выполняются оба условия четности функции, заключаем, что функция  – четная.
– четная.
Преобразования графиков
Приведем графики некоторых функций:
1)  – прямая линия; 2)
– прямая линия; 2)  – квадратичная парабола;
– квадратичная парабола;
3)  – кубическая парабола; 4)
– кубическая парабола; 4)  – гипербола;
– гипербола;
5)  – график квадратного корня;
– график квадратного корня;
Правила преобразования графиков:
Пусть дана функция 
1. Для построения графика функции  исходный график функции
исходный график функции  симметрично отображаем относительно оси Ох (рис. 1).
симметрично отображаем относительно оси Ох (рис. 1).
2. Для функции 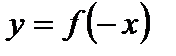 заданный график симметрично отображаем относительно оси Оу (рис. 2).
заданный график симметрично отображаем относительно оси Оу (рис. 2).
Рис. 1 Рис. 2
3. Для функции  этот график получается параллельным переносом графика функции
этот график получается параллельным переносом графика функции 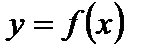 на
на  масштабных единиц вдоль оси Оу вверх, если
масштабных единиц вдоль оси Оу вверх, если 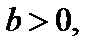 и вниз, если
и вниз, если  (рис. 3).
(рис. 3).
4. Для функции  этот график получается параллельным переносом графика функции
этот график получается параллельным переносом графика функции  на
на  масштабных единиц вдоль оси Ох вправо, если
масштабных единиц вдоль оси Ох вправо, если  и влево, если
и влево, если  (рис. 4).
(рис. 4).
Рис. 3 Рис. 4
5. Для функции  где
где  график функции
график функции 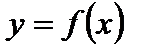 «растянут» в k раз вдоль оси Оу (от оси Ох), если
«растянут» в k раз вдоль оси Оу (от оси Ох), если  «сжат» в
«сжат» в  раз вдоль оси Оу (к оси Ох), если
раз вдоль оси Оу (к оси Ох), если  (рис. 5).
(рис. 5).
Рис. 5
6. Для функции  где
где  график
график  «растянут» вдоль оси Ох (от оси Оу) в
«растянут» вдоль оси Ох (от оси Оу) в  раз при
раз при  «сжат» вдоль Ох (коси Оу) в m раз, при
«сжат» вдоль Ох (коси Оу) в m раз, при  (рис. 6).
(рис. 6).



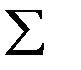 .Факториал.
.Факториал.
 называется многочленом n-й степени от одной переменной х, записанным в стандартном виде.
называется многочленом n-й степени от одной переменной х, записанным в стандартном виде. называются коэффициентами данного многочлена,
называются коэффициентами данного многочлена, 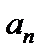 – старшим коэффициентом,
– старшим коэффициентом,  – свободным членом. Число
– свободным членом. Число 
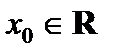 называется корнем многочлена
называется корнем многочлена  если
если 
 точки М. Обратно, любой точке М (а, b) плоскости соответствует комплексное число z = a + bi. Плоскость, точки которой отождествляются с комплексными числами, называют комплексной плоскостью, где ось Ох называется действительной осью, Оу – мнимой осью.
точки М. Обратно, любой точке М (а, b) плоскости соответствует комплексное число z = a + bi. Плоскость, точки которой отождествляются с комплексными числами, называют комплексной плоскостью, где ось Ох называется действительной осью, Оу – мнимой осью.
 ) + isin (π +
) + isin (π +  )=
)=  .
. = a - bi.
= a - bi. .
.

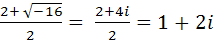 ,
, .
.

 возвести в 9-ую степень по правилам действия над комплексными числами в алгебраической форме, то мы не достигнем необходимого результата. В данном случае сначала комплексное число представим в тригонометрической форме, а затем уже возведем в степень. Найдем модель и аргумент комплексного числа z = 1 + i
возвести в 9-ую степень по правилам действия над комплексными числами в алгебраической форме, то мы не достигнем необходимого результата. В данном случае сначала комплексное число представим в тригонометрической форме, а затем уже возведем в степень. Найдем модель и аргумент комплексного числа z = 1 + i  = 2,
= 2, =
= 
 2(cos
2(cos  )
) 
 + isin
+ isin  - модуль комплексного числа,
- модуль комплексного числа, ,
, =
=  ,
, ?
? ;
;  ;
;  .
. п (читается т на п).
п (читается т на п).
 .
.
 - a12
- a12  + a13
+ a13 
 = а11 . а22 . а33 + а12 . а23 . а31 + а13 . а21 . а32 – а13 . а22 . а31 –
= а11 . а22 . а33 + а12 . а23 . а31 + а13 . а21 . а32 – а13 . а22 . а31 –
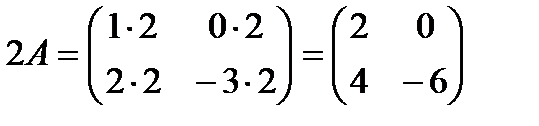


 и
и  .
.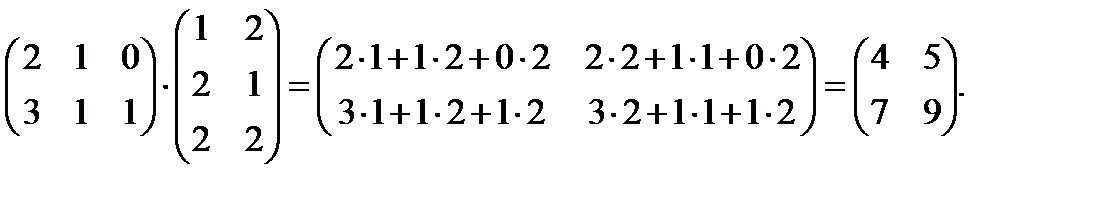

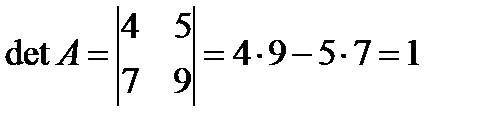

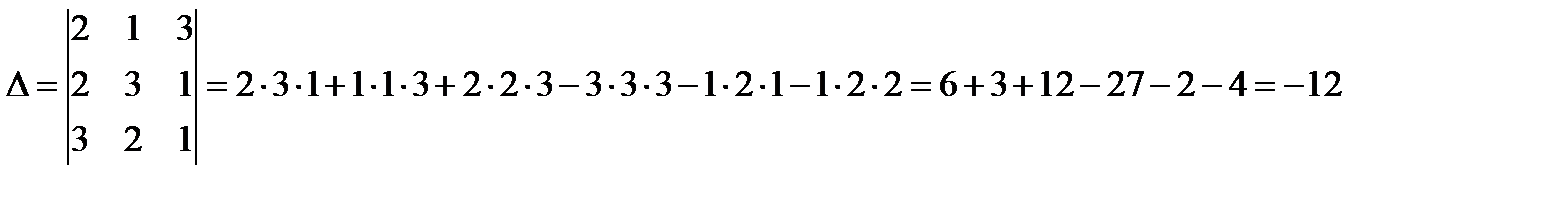
 = 1 .
= 1 .  - 2 .
- 2 . 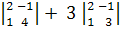 = 2.
= 2. = 5 .
= 5 .  = 2,
= 2,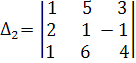 = 1 .
= 1 . 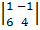 - 5 .
- 5 .  = - 2,
= - 2, = 1 .
= 1 .  - 2 .
- 2 .  = 4.
= 4. ,
,  .
.





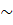
 ⇔
⇔  ⇔
⇔ 









 по некоторому правилу f ставится в соответствие единственный элемент
по некоторому правилу f ставится в соответствие единственный элемент 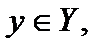 то говорят, что задана функция. Обозначается
то говорят, что задана функция. Обозначается  где х – аргумент или независимая переменная функции; у – значение функции или зависимая переменная.
где х – аргумент или независимая переменная функции; у – значение функции или зависимая переменная.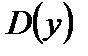 или
или 
 или
или 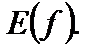
 при заданном частном значении аргумента
при заданном частном значении аргумента 
 обозначается
обозначается 
 называется множество всех точек плоскости с координатами
называется множество всех точек плоскости с координатами  где
где 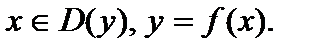
 называется четной, если:
называется четной, если: – симметричное множество относительно
– симметричное множество относительно 
 выполняется равенство
выполняется равенство 
 называется нечетной, если:
называется нечетной, если: – симметричное множество относительно
– симметричное множество относительно 
 выполняется равенство
выполняется равенство 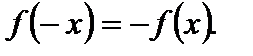
 является четной или нечетной, то говорят, что она обладает свойством четности.
является четной или нечетной, то говорят, что она обладает свойством четности. график нечетной – относительно начала координат.
график нечетной – относительно начала координат. с областью определения
с областью определения  называется периодической, если существует такое число
называется периодической, если существует такое число  что для любого значения
что для любого значения  выполняются условия:
выполняются условия:

 функции
функции  такие, что
такие, что 
 то функция называется возрастающей;
то функция называется возрастающей; – убывающей;
– убывающей; – неубывающей;
– неубывающей; – невозрастающей.
– невозрастающей. или
или  ), называются промежутками знакопостоянства.
), называются промежутками знакопостоянства.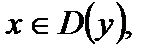 при которых функция
при которых функция 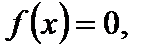 называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.

 (3.1)
(3.1) множество точек.
множество точек. равносильно неравенству
равносильно неравенству

 означает, что
означает, что  т. е.
т. е. 
 Получаем
Получаем 






 Вычисляем значение функции в этой точке:
Вычисляем значение функции в этой точке:  Следовательно,
Следовательно, 

 имеет
имеет  Следовательно, функция определена на симметричном множестве.
Следовательно, функция определена на симметричном множестве.
 – четная.
– четная. – прямая линия; 2)
– прямая линия; 2)  – квадратичная парабола;
– квадратичная парабола; – кубическая парабола; 4)
– кубическая парабола; 4)  – гипербола;
– гипербола;

 – график квадратного корня;
– график квадратного корня;
 исходный график функции
исходный график функции  симметрично отображаем относительно оси Ох (рис. 1).
симметрично отображаем относительно оси Ох (рис. 1).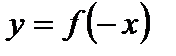 заданный график симметрично отображаем относительно оси Оу (рис. 2).
заданный график симметрично отображаем относительно оси Оу (рис. 2). этот график получается параллельным переносом графика функции
этот график получается параллельным переносом графика функции 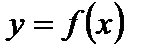 на
на  масштабных единиц вдоль оси Оу вверх, если
масштабных единиц вдоль оси Оу вверх, если 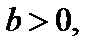 и вниз, если
и вниз, если  (рис. 3).
(рис. 3). этот график получается параллельным переносом графика функции
этот график получается параллельным переносом графика функции  на
на  масштабных единиц вдоль оси Ох вправо, если
масштабных единиц вдоль оси Ох вправо, если  и влево, если
и влево, если  (рис. 4).
(рис. 4). где
где  график функции
график функции 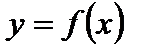 «растянут» в k раз вдоль оси Оу (от оси Ох), если
«растянут» в k раз вдоль оси Оу (от оси Ох), если  «сжат» в
«сжат» в  раз вдоль оси Оу (к оси Ох), если
раз вдоль оси Оу (к оси Ох), если  (рис. 5).
(рис. 5). где
где  график
график  «растянут» вдоль оси Ох (от оси Оу) в
«растянут» вдоль оси Ох (от оси Оу) в  раз при
раз при  «сжат» вдоль Ох (коси Оу) в m раз, при
«сжат» вдоль Ох (коси Оу) в m раз, при  (рис. 6).
(рис. 6).


