Федяев О. И.
Элементарная геометрия
Часть I
Лекции по специальному курсу
Элементарной математики
Учебное пособие
для студентов педагогических вузов
Москва - 2010
УДК 514.1
ББК 22.151.0
Печатается по решению кафедры высшей алгебры,
элементарной математики и методики преподавания
математики и редакционно-издательского совета МГОУ
Федяев О. И. Элементарная геометрия. Часть I Лекции по специальному курсу элементарной математики. Учебное пособие для студентов педагогических вузов. – М., Издательство МГОУ, 2009, с.
Материал пособия разбит на шесть частей, называемых лекциями. В каждой из них рассматриваются основные вопросы соответствующего раздела элементарной геометрии, акцентируется внимание читателя на основных фактах этих разделов. В разделе «Введение» дан общий обзор истории возникновения и развития так называемой «Евклидовой геометрии».
Научный редактор: проф. Рассудовская М. М.
Рецензенты: проф. Куланин Е. Д.
доц. Птицына И. В.
ã Московский государственный
областной университет, 2009
Предисловие.
Курс «Элементарной геометрии» – третья часть Специального курса элементарной математики, который изучается студентами педагогических ВУЗов, готовящихся стать учителями математики. Его целью является, с одной стороны, углубленное изучение основных фактов евклидовой геометрии, элементы которой составляют основное содержание школьного курса геометрии, а с другой – демонстрация роли и значения геометрических преобразований в этой геометрии.
Эти задачи курса определили и его структуру: первая часть – обзор основных фактов евклидовой геометрии, вторая – систематическое исследование места геометрических преобразований в этой геометрии. Естественно, что характер определенной оригинальности пособия связан с этой структурой: если в первой части она проявляется в методическом подходе и выборе тем разделов, то во второй части она связана не только со структурой изложения, но и с принципиально иными способами решения и представления конкретных фактов, определяющих эту структуру.
Автор считал необходимым формировать у будущего учителя математики интерес и умения критического анализа учебной и методической литературы, что невозможно осуществлять без глубоких знаний своего предмета. Именно эта цель, в первую очередь, определила характер избранных тем и последовательность их представления в пособии.
Кроме того, компактность изложения – дань требованию учебного плана, который на такой содержательный курс, крайне необходимый будущему учителю, отводит всего 24 часа аудиторного времени. Несомненно, читатель или студент, изучающий специальный курс «Элементарной математики» должен быть готов к серьезной самостоятельной работе, которая только и может обеспечить овладение этим основным для будущего учителя математики предметом.
Введение
Основные содержательные геометрические понятия и факты, принадлежащие так называемой евклидовой геометрии, своими корнями и происхождением уходят в глубокую древность и порождены потребностью в решении задач сугубо практического характера, вызванных к жизни естественными нуждами человеческого сообщества. В своем развитии вместе с усложнением общественных отношений, возникновением структур их регулирования, развитием производственной и духовной культуры складывались условия, вызвавшие к жизни потребности не-только и нестолько практического характера, но прежде всего умственного, духовного порядка, которые способствовали возникновению и формированию геометрической системы понятий и фактов, лишенных материальной основы, смысл которых состоит не столько в их практической приложимости, сколько в их логической связи, логической соподчиненности. Именно такого рода духовная, интеллектуальная потребность человека привела к возникновению геометрии как научной системы, в которой все понятия и факты структурированы и расположены в порядке их логических связей, логической соподчиненности. Именно в таком виде предстает геометрия в бессмертном творении Евклида под названием «Начала», именно здесь все начинается с основных понятий и фактов, а всякое утверждение выводится в соответствии с законами логики из этих понятий и фактов, истинность утверждения доказывается, а не проверяется опытным путем. «Начала» Евклида – первое из дошедших до нас подлинно научное сочинение в этой области.
Первые математические факты были накоплены в период с третьего по первое тысячелетия до нашей эры, прежде всего, в Вавилоне и Египте. Вавилоняне далеко ушли в области числового счисления (шестидесятеричная система), алгебры и геометрических вычислений. Египтяне же имели менее приспособленную систему счисления и в алгебре отстали, но геометрические задачи, которыми они занимались, требовали гораздо более значительных геометрических познаний. Однако, логическая обработка накопленного материала отсутствовала, математические сведения представляли лишь свод правил решения некоторых конкретных задач практического характера.
Появление геометрии в Греции согласно Проклу (410-485 г.г. н. э.), комментатору «Начал» Евклида, связано с именем Фалеса Милетского (7-6 столетия до н. э.). В Греции сложилась возможность уйти от утилитарной потребности в геометрических фактах и акцентировать внимание на далеко идущей абстракции, от геометрии измерения перейти к учению о пространственных формах. Уже в следующем столетии после Фалеса большие успехи в этом направлении были достигнуты Пифагором и его школой (6-5 в.в. до н. э.). Метафизический характер рассуждений способствовал формированию потребности в абстрагировании и возникновению абстрактных понятий.
Требование логического обоснования геометрии связывают с именем Платона, первого философа идеалистического направления (5-4 столетия до н. э.). Согласно Платону во главу всякой отрасли знания и деятельности должны быть поставлены понятия и положения, из которых все остальное вытекает как следствие по законам логики. Основная установка Платона, научное обоснование всякого знания, крепла в течении всей истории развития науки и была существенно развита и углублена в первую очередь его учеником Аристотелем (384-322 гг. до н. э.). Именно он становится действительным родоначальником настоящей науки. Сама теория логического вывода принадлежит Аристотелю («Органон» – собрание сочинений Аристотеля, составленное Андроником Родосским в середине 1-го столетия до н. э.). Таким образом, уже в 4-ом веке до н. э. была установлена логическая схема, по которой должна строиться всякая выводная наука. Именно она и реализована в знаменитых «Началах» Евклида Александрийского (4-3 в.в. до н. э.). В контексте исторического процесса развития математических знаний «Начала» Евклида предстают образцом их научного построения в соответствии с требованиями Аристотелевской логики. Греческий текст «Начал» дошел до нас в большом числе манускриптов, большинство из которых ведет свое начало от Теона Александрийского, жившего в Александрии в 4-ом в. н. э. и преподававшего математику по Евклиду. Первое издание «Начал» в Европе появилось в 1482 году в Венеции и выпущено Ратдольтом, основавшим там крупное по тем временам издательство. «Начала» Евклида в течении веков служили учебным источником математических знаний для многих поколений учащихся. До середины 19 века в Англии и Германии изучали геометрию по школьным изданиям «Начал» и даже в начале 20 века можно было ещё встретить английские школы, в которых «Начала» оставались учебным пособием. Таким образом, именно «Начала» Евклида можно считать первоисточником становления и развития математических знаний, первоисточником мощного метода научного познания, во многом определившего ход развития не только математики, но и мировой науки в целом.
«Начала» состоят из тринадцати книг, из которых первые шесть посвящены тому, что мы называем планиметрией. Книги с 7-ой по 9-ую содержат начала теории чисел (Элементы учения о целом числе). Книга 10-я – геометрическая теория иррациональных величин, 11-13 книги содержат стереометрический материал. К тринадцати книгам «Начал» примыкают две монографии, обыкновенно называемые их 14-ой и 15-ой книгами. Однако, как выяснилось одна принадлежит Гипсиклесу Александрийскому, ученику Евклида, автор же другой книги остался неизвестным.
Каждая книга «Начал» начинается с определений всех понятий, которые в ней впервые появляются, первой книге предпосланы аксиомы и постулаты. Изложение всех предложений-теорем строится по совершенно единой схеме: оно начинается формулировкой утверждения, за которой следует доказательство, в целом, имеющее тот же смысл и структуру, что и в наше время. Изложение носит строго догматический характер, автор излагает читателю содержание теоремы и развертывает перед ним доказательство. Характер всего сочинения сугубо теоретический. «Начала» не содержат того, что выражает само название математической теории – прямой метрики, т. е. теорем, устанавливающих в числах длины, площади и объемы фигур.
В своей структуре это сочинение несет явный отпечаток установок Платона и Аристотеля и для своего времени и, многих столетий спустя, отличается удивительным совершенством. «Неоспоримая крепость их догматов и их совершенство настолько абсолютны, что никакое другое сочинение по справедливости нельзя с ним сравнивать. Вследствие этого в них отражается такой свет истины, что, по-видимому, только тот способен отличать в сложных вопросах геометрии истинное от ложного, кто усвоил Евклида»(Г. Кардано,1501-1576 г.г.).
Несмотря на высокие достоинства «Начал», они вызывали и большое число возражений и обстоятельную критику со стороны математиков последующих за их появлением столетий. При всей последовательности структуры «Начал», при огромной роли в них логических выводов, сочинение Евклида все же не представляет выдержанной дедуктивной системы, как того требует аристотелевская схема. Рассуждения Евклида представляют собой смесь логических выводов и соображений основанных на наглядных представлениях, смесь логики и интуиции. Вследствие этого, вместе с их всеобщим признанием начинается и систематическая критика. Эта критика, с одной стороны, выявляет многие дефекты «Начал», а с другой приводит к осознанию существа аксиоматического метода и созданию образцов безупречной аксиоматики.
Первым крупным достижением в области аксиоматического построения геометрии явилось исследование Паша «Лекции по новой геометрии» (1882 год). Паш считал, что основные положения геометрии должны быть заимствованы из опыта, но выводы из них осуществляются только путем логических умозаключений. Паш подошел очень близко к системе аксиом, достаточной для логического построения геометрии, однако в его аксиоматической системе сильно преувеличено число аксиом, нужных, например, для установления порядка точек, его система не обладает структурой, позволяющей отчетливо структурировать и систему следствий.
Вторым значительный вклад в аксиоматическое обоснование евклидовой геометрии внес итальянский математик Пеано своей работой «Логически изложенные основания геометрии» (1889 г.). У Пеано, однако, нет полной аксиоматической системы, им даны лишь аксиомы соединения и порядка. Зато в этой ограниченной области он достиг логической отточенности изложения.
Ученик Пеано Пиери стремился свести к минимуму число основных понятий, оставляя только два: точка и движение («Элементарная геометрия как дедуктивная система», 1893 год). Однако, стремясь к формальному упрощению системы основных понятий, он усложнил свою аксиоматику по существу. Многие из его аксиом очень тяжеловесны. Чрезмерно сократив число основных понятий, Пиери был вынужден вводить изгнанные понятия посредством искусственных и громоздких определений. В следствие этого исчезло естественное логическое членение аксиоматики по областям действия основных понятий, усложнились логические связи, система, в целом, приобрела тяжеловесный и трудно воспринимаемый вид.
Первое издание работы Д. Гильберта «Основания геометрии» появляется в 1899 году. В отличии от своих предшественников Гильберту удалось создать аксиоматическую систему настолько удачно расчлененную, что логическая структура геометрии предстала совершенно прозрачной, аксиомы сформулированы наиболее простым и кратким образом и так расчленены на отдельные группы, что становится возможным видеть как далеко можно развивать их следствия, обнаружить естественное логическое членение всей системы их следствий. Одновременно был проведен логический анализ, выявляющий роль отдельных групп аксиом.
Прежде всего, принципиально важен отказ Гильберта от толкования прямых и плоскостей как бесконечных множеств, составленных из точек. У него точка, прямая и плоскость – самостоятельные понятия. В формулировках аксиом и в доказательствах теорем фигурирует лишь конечное число точек, прямых, плоскостей и понятие о бесконечном множестве остается праздным. Разбиение прямой на две части какой-либо принадлежащей ей точкой нет необходимости мыслить как разбиение точечного множества, достаточно лишь иметь возможность ответить на вопрос: лежат ли две произвольные точки прямой по одну или по разные стороны от фиксированной точки. Рассматривая шаг за шагом всю гильбертовскую систему, мы убеждаемся, что везде речь идет лишь о конечных конструкциях, законы которых дают нам аксиомы, ничто не принуждает нас прибегать к теории множеств.
Однако, совсем иначе обстоит дело с теми следствиями, которые опираются (или должны опираться) на аксиомы непрерывности (у Гильберта – это пятая группа аксиом). Эти аксиомы существенно предполагают, что речь идет о бесконечном множестве. Теоретико-множественная точка зрения оказывается лежащей в самой основе соответствующих понятий. Принимая аксиомы непрерывности, мы вынуждены иметь в поле зрения бесконечные множества, что вносит существенную неясность: хотим обосновать геометрию, а между тем используем понятия другой математической теории, которая сама нуждается в обосновании. В результате возникает необходимость расширения круга исследований, полная прозрачность конечных конструкций исчезает. Крупнейшим достижением Гильберта в области логического анализа геометрии как раз и явилось то, что он обнаружил возможность развития геометрии во всем существенном без обращения к аксиомам непрерывности.
С точки зрения завершенности анализа геометрической системы Евклида «Основания геометрии» Д. Гильберта поставили точку в вопросе полноты решения этой проблемы. В них представлены не только достаточные аксиоматические основания для формально-логического развития теории в целом, но и обеспечено естественное структурирование системы их следствий, возникает отчетливая картина связей между фундаментальными геометрическими системами. Педагогически важно и то, что базовые (основные) понятия гильбертовской аксиоматики, отвечая наглядному восприятию геометрических образов и их отношений, наиболее полно и естественно обеспечивают овладение не только содержательными фактами евклидовой геометрии, но и служат наиболее естественным средством обучения учащихся дедуктивному методу, лежащему в основе практически любого научного знания.
Результаты, достигнутые Гильбертом не остановили, однако, работу в области оснований геометрии и в его время и позднее вплоть до наших дней были предложены и другие варианты аксиоматических систем евклидовой геометрии. С одной стороны, это было следствием общего развития математики, поставившего задачу единого подхода к обоснованию геометрии в целом, а с другой – стремлением к осовремениванию и школьного курса математики и геометрии в частности через введение в него понятий и целых тем, отражающих базовые понятия современной математики. Соответствующие варианты аксиоматического построения геометрии Евклида на сегодняшний день можно разделить на три базовые случая, которые естественно связываются с именами Д. Гильберта, Г. Вейля и Ф. Бахмана. Предложенные ими аксиоматические системы будут в обзорном порядке рассмотрены нами в заключительной части курса.
Цели и задачи нашего обзорного по характеру курса элементарной геометрии не обязывают следовать той или иной точке зрения на построение современного школьного курса геометрии, но вынуждают акцентировать внимание на идейном значении центральных понятий и фактов и их логической взаимосвязи. Это прежде всего касается таких понятий современной математики как геометрическое преобразование и вектор. Содержательные факты евклидовой геометрии с учетом характера их представления в школьном курсе целесообразнее всего рассматривать в традиционном стиле, т. е. на базе аксиоматики Д. Гильберта или близкой к ней. Поэтому читатель вполне может считать основаниями нашего курса аксиоматическую систему Гильберта, хотя это и не означает скрупулезность вывода её следствий. Прежде всего это находит отражение в выборе базовых (основных неопределяемых) понятий, которыми как и у Гильберта у нас являются «точка», «прямая», «плоскость», «принадлежность (инцидентность)», «лежать между», «конгруэнтность».
Лекция 1.
Аксиомы.
1. Точка есть фигура.
2. Если из М  F 1 следует M
F 1 следует M  F 2, а из N
F 2, а из N  F 2 следует N
F 2 следует N  F 1, то F 1 и F 2 – различные обозначения одной и той же фигуры. В этом случае говорим, что F 1 равна F 2 и пишем F 1 = F 2.
F 1, то F 1 и F 2 – различные обозначения одной и той же фигуры. В этом случае говорим, что F 1 равна F 2 и пишем F 1 = F 2.
3. Фигура F существует, если существует хотя бы одна точка, принадлежащая фигуре F.
Последняя аксиома предполагает заданным условие, позволяющее решать вопрос о принадлежности точки фигуре, при этом, естественно, что это условие должно быть выражено в терминах рассматриваемой геометрической системы. Так как принадлежность точки прямой или плоскости проверяема с точки зрения гильбертовской аксиоматики, то прямые и плоскости мы относим к геометрическим фигурам. Для задания прямой в геометрии Евклида достаточно указать две точки, для задания плоскости – три точки общего положения, для задания окружности или сферы – три, или соответственно четыре точки общего положения и т.д. и т.п.
Как фигура может быть задана? Первое – путем указания набора точек, который позволит решить вопрос о принадлежности произвольной точки рассматриваемой фигуре. Второе – путем задания так называемого характеристического свойства точек, принадлежащих фигуре. Это свойство, во-первых, выражается в терминах рассматриваемой теории, а во-вторых, определяет фигуру в том смысле, что позволяет решать вопрос о принадлежности точки фигуре: всякая точка пространства принадлежит фигуре тогда и только тогда, когда она обладает указанным свойством. Если фигура задается характеристическим свойством точек, ей принадлежащих, то она со времен Евклида, имеет название геометрического места точек.
О фигурах, как геометрических местах точек, поговорим позднее, а сейчас обратимся к трем понятиям, которые в учебных курсах геометрии используются без определений.
2º. Тело, поверхность, линия.
Прежде всего заметим, что эти понятия в отличии от понятия «фигура» – понятия определяемые, но их определения зависят от той трактовки, которая характерна для соответствующей математической теории. В евклидовой геометрии эти понятия трактуются со времен Евклида как: ограниченная часть пространства – тело, граница тела – поверхность и соответственно линия – граница поверхности. Используя именно такие, хотя и расплывчатые, представления об этих фигурах, покажем, как они могут быть определены в терминах евклидовой геометрии.
Основным понятием, которое мы используем в определениях понятий тело, поверхность, линия, будет понятие окрестности точек, трактуемое как открытый шар, то есть шар без точек его поверхности, центром которого является сама рассматриваемая точка. При этом сам термин «шар» имеет значение, зависящее от размерности пространства, в котором рассматривается точка и ее окрестность. Для пространства одномерного (прямой) этот «шар» называют интервалом, для случая двумерного пространства (плоскости) «шар» - это круг с центром в рассматриваемой точке. В трехмерном пространстве или как мы говорим просто «в пространстве» «шар» - это соответствующая пространственная фигура хорошо знакомая читателю. Таким образом, окрестность точки О есть фигура, каждая точка которой удалена от О на расстояние, меньшее заданной величины r (отрезка r). При необходимости окрестность точки О можно обозначить парой (О, r). Саму точку О можно отнести к ее окрестности
Определение. Фигуру F пространства называют телом, если она представляет собой ограниченную, замкнутую область пространства.
Раскроем содержание понятий замкнутая и ограниченная область. Для этого придется ввести ряд понятий, которые мы сейчас последовательно рассмотрим.
Понятие первое: точка М называется точкой сгущения фигуры F, если в любой ее окрестности содержатся точки этой фигуры.
Обратим внимание на то, что сама точка М может как принадлежать фигуре F, так ей и не принадлежать.
Пример: F – шар. Внутренняя точка шара – точка сгущения принадлежит шару, точка поверхности шара – точка сгущения шара вне зависимости от того какой шар мы рассматриваем: вместе с его поверхностью или без нее. В первом случае – это точка шара, а во втором – она ему не принадлежит. Таким образом, точка сгущения фигуры может как принадлежать так и не принадлежать самой фигуре.
Второе понятие: F называется замкнутой фигурой, если она содержит все свои точки сгущения.
Третье понятие: F- связная фигура, если любые две ее точки можно соединить ломаной линией, каждая точка которой принадлежит фигуре F.
Четвертое понятие: Фигура F называется ограниченной, если существует шар, которому принадлежит каждая точка фигуры F.
Примерами неограниченных фигур являются прямая, плоскость, луч, полуплоскость.
Пятое понятие: М – внутренняя точка фигуры F, если М  F и существует окрестность точки М, принадлежащая фигуре F.
F и существует окрестность точки М, принадлежащая фигуре F.
Если есть окрестность точки М, никакая точка которой не принадлежит F, то М – внешняя точка для фигуры F. Если в любой окрестности М имеются точки, принадлежащие F и точки ей не принадлежащие, то М называем граничной точкой F. Сама граничная точка может принадлежать F, а может ей и не принадлежать. Фигура, каждая точка которой является граничной точкой фигуры F, называется границей F. У замкнутой фигуры ее граница принадлежит фигуре, а у незамкнутой граница ей не принадлежит.
Шестое понятие: Область пространства – связная ограниченная фигура, каждая точка которой является ее внутренней точка.
Перечисленные понятия полностью раскрывают содержание понятия «тело» в том смысле, в каком оно используется, по крайней мере, в евклидовой геометрии. Примером тел, изучаемых в школьном курсе геометрии, являются призмы, пирамиды и тела вращения. Соответствующие фигуры с теми же названиями рассматриваются и как поверхности: говорят о цилиндрической, конической, сферической поверхностях, поверхностях призм и пирамид.
Понятие поверхности, в наглядном смысле трактуемое как граница тела, может быть раскрыто по той же схеме и с использованием тех же вспомогательных понятий, которые мы использовали в определении понятия «тело». Поэтому позволим себе представить это понятие в обзорном порядке.
Определение 1: Фигура F называется полной поверхностью, или оболочкой, если она является границей некоторого тела Т.
Поверхность рассматривается как часть оболочки некоторого тела. Для формального определения этого понятия вводится понятие внутренней точки такой фигуры, ее граничной точки и границы этой фигуры, а также понятие связности фигуры, принадлежащей оболочке.
Фигура Х называется областью на оболочке F, если все ее точки являются внутренними точками оболочки, а сама фигура Х является связной на F. Область Х на F замкнута, если ей принадлежат все ее граничные точки. Отсюда получаем.
Определение 2: Фигура Р называется поверхностью, если существует такая область Х на оболочке F, замыкание которой и есть фигура Р.
Говоря об определении линии, мы имеем в виду лишь такую линию, которая может быть границей поверхности. В современной математике понятие линии значительно расширено и его наиболее общее определение связано с понятием одномерного многообразия как топологического образа ломаной линии.
Если Р – какая-либо поверхность, то можно говорить о границе этой поверхности как фигуре, содержащей граничные точки поверхности Р. Но в этом случае фигура Р будет представлять замкнутую линию, в то время как очень часто приходится рассматривать и незамкнутые линии. Значит, следует определять это понятие так, чтобы и этот случай не был потерян.
Назовем границу поверхности ее полным контуром, тогда фигура F принадлежащая контуру поверхности Р, называется линией, если F – такая область на Р, замыканием которой служит сама фигура F.
Определения понятию «линия» в современном расширенном смысле впервые были даны Г.Кантором (1845 - 1918 г.г.) и П.С.Урысоном (1898 – 1924 г.г.), причем Урысон обобщает определение Кантора (см., например, А.С.Пархоменко, «Что такое линия?», М. 1954г.).
3º. Некоторые геометрические места точек.
Рассмотрим примеры фигур, которые определяются как геометрические места точек. Договоримся для удобства сокращать это название и писать «г.м.т.».
Первыйклассг.м.т. В определениях г.м.т. этого класса используется как основное, понятие «расстояние». При этом под расстоянием от точки М до фигуры F будем понимать наименьший из всех отрезков, соединяющих точку М с каждой точкой фигуры F.
Рассмотрим примеры двух типов таких г.м.т.
1-й тип – г.м.т., каждая из которых удалена от данной фигуры F на заданное расстояние h. Выбирая конкретные F и h, мы обращаемся к конкретному г.м.т.
Пример 1. Фигура – точка О, расстояние – конкретный отрезок h.
В этом случае наше г.м.т. есть известная фигура – окружность, в случае, когда мы рассматриваем г.м.т. в плоскости, (двумерном пространстве), сфера, если речь идет о г.м.т. в пространстве (трехмерном пространстве). О – центр окружности, или сферы соответственно, h – их радиус, обозначение – (О, h).
Пример 2. Фигура – прямая а, расстояние – отрезок h. Рассматривается г.м.т., каждая из которых удалена от а на расстояние h.
Если рассматриваем это г.м.т. в двумерном пространстве, то оно представляет собой пару прямых, параллельных прямой а, расположенных по разные стороны от а (рис. 1).

Рис. 1
Прямые, составляющие г.м.т., изображены штриховой линей. Доказательство проводить не будем, но отметим его шаги:
1. Доказывается существование точки, удаленной от а на расстояние h;
2. Через полученную точку (например, Mi) проводится прямая  , параллельная прямой а, а через Ni проводится прямая n, параллельная а.
, параллельная прямой а, а через Ni проводится прямая n, параллельная а.
3. Доказывается, что всякая точка г.м.т. принадлежит либо m, либо n, а всякая точка этих прямых принадлежит г.м.т.
На этом основании и делается заключение, что г.м.т. есть пара прямых (m, n).
Пример 3. Г.м.т. плоскости, удаленных на данное расстояние h от данного отрезка АВ.
Это г.м.т. представляет собой пару отрезков M 1 N 1 и M 2 N 2 и пару полуокружностей с центрами А и В и радиусами равными h. Эту фигуру можно назвать «беговой дорожкой» (рис. 2).

Рис. 2
Для исследования вида этого г.м.т. целесообразно через точки А и В провести перпендикуляры к прямой АВ в концах данного отрезка и исследовать наличие точек, удаленных от отрезка АВ на расстояние h в полосе между перпендикулярами и в двух полуплоскостях, для которых эти перпендикуляры – граничные прямые и точки отрезка АВ этим полуплоскостям не принадлежат. В полосе часть г.м.т. – это пара отрезков M 1 N 1 и M 2 N 2, а в полуплоскостях – это дуги окружностей (A, h) и (B, h).
Пример 4. Г.м.т. плоскости, удаленных на расстояние h от данной окружности (O, R).
 Рассмотрим этот пример подробнее. Будем решать вопрос о существовании точек этого г.м.т., разделив плоскость на две части: область, ограниченную окружностью и область, точки которой лежат вне круга, ограниченного окружностью. Так как точки, лежащие в первой области (круге), удалены от окружности (O, R) на расстояние, меньшее R, а точки, лежащие вне круга (O, R), находятся от нее на расстоянии большем R, то следует рассматривать три случая соотношения между h и R: h < R, h = R и h > R.
Рассмотрим этот пример подробнее. Будем решать вопрос о существовании точек этого г.м.т., разделив плоскость на две части: область, ограниченную окружностью и область, точки которой лежат вне круга, ограниченного окружностью. Так как точки, лежащие в первой области (круге), удалены от окружности (O, R) на расстояние, меньшее R, а точки, лежащие вне круга (O, R), находятся от нее на расстоянии большем R, то следует рассматривать три случая соотношения между h и R: h < R, h = R и h > R.
В первом случае, очевидно, что точки, удаленные от (O, R) на расстояние h, существуют как внутри круга(O, R), так и вне его (рис. 3).
1. Фиксируем какой-нибудь радиус ОА. От точки А откладываем в направлении к О на радиусе ОА отрезок  . Получаем точку М 1, лежащую внутри круга (O, R) на расстоянии h от окружности.
. Получаем точку М 1, лежащую внутри круга (O, R) на расстоянии h от окружности.
2. Точно так же откладываем на луче ОА от точки А вне круга (O, R) отрезок  . Получаем точку М 2 вне (O, R), которая удалена от окружности на расстояние h.
. Получаем точку М 2 вне (O, R), которая удалена от окружности на расстояние h.
Точка любой из окружностей (O, R - h) и (O, R + h) удалена от (O, R) на расстояние h.
Обратное, любая точка M i, удаленная от окружности (O, R) на расстояние h, принадлежит одной из окружностей (O, R - h) или (O, R + h). Таким образом, в рассматриваемом случае исследуемое г.м.т. есть пара окружностей (O, R - h) и (O, R + h).
Во втором случае, когда  , г.м.т. состоит из точки О и окружности (O, R + h).
, г.м.т. состоит из точки О и окружности (O, R + h).
В третьем случае г.м.т. содержит только точки, лежащие вне круга (O, R), и представляет собой окружность (O, R + h).
В качестве упражнения для самостоятельной работы рекомендуем обобщить рассмотренные примеры, рассмотрев г.м.т. с тем же определением, но в трехмерном пространстве.
Перейдем к примерам г.м.т. 2-ого типа.
2-й тип г.м.т. первого класса – это г.м.т., каждая из которых равноудалена от двух данных фигур F 1 и F 2.
Как и в предыдущем случае, задавая конкретные фигуры F 1 и F 2, получаем конкретные г.м.т. второго типа.
Пример 1. Фигура F 1 – точка А, фигура F 2 – точка В.
Речь пойдет о г.м.т., равноудаленных от точек А и В. Используем, как известный факт, вопрос о существовании середины отрезка. Итак, пусть О – середина отрезка АВ. Тогда О – точка, равно удаленная от точек А и В. Проведем через О перпендикуляр к прямой АВ и обозначим его буквой m (рис. 4).
 Пусть M – произвольная точка m, отличная от О. Тогда из равенства прямоугольных треугольников АОМ и ВОМ следует
Пусть M – произвольная точка m, отличная от О. Тогда из равенства прямоугольных треугольников АОМ и ВОМ следует  , то есть М равноудалена от данных точек А и В.
, то есть М равноудалена от данных точек А и В.
Вывод: прямая m входит в состав исследуемого г.м.т.
Теперь покажем, что любая точка равноудаленная от А и В, принадлежит перпендикуляру m. Допустим противное, то есть N равноудалена от А и В, но 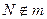 .
.
1. из допущения и равенства треугольников AON и BON, а также смежности углов  и
и  следует ортогональность прямых ON и AB. В результате
следует ортогональность прямых ON и AB. В результате
2. имеем два различных перпендикуляра m и ON к прямой АВ, которые проходят через одну точку О. Это противоречит известному факту геометрии Евклида. Такой результат – следствие сделанного выше допущения, значит оно неверно. Таким образом, из двух возможностей  и
и 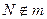 верна только первая.
верна только первая.
Вывод: Исследуемое г.м.т. есть прямая, перпендикулярная к отрезку, соединяющему точки А и В, в его середине.
Это г.м.т. часто называют «серединным перпендикуляром отрезка», по-гречески – медиатриса отрезка.
Пример 2. Фигуры F 1 и F 2 – два луча h и k, имеющие общее начало О. Такая пара лучей, как известно, называется углом. Поэтому можно говорить о г.м.т., равноудаленных от сторон угла  . Здесь, как и выше, будем вести речь о г.м.т. в плоскости.
. Здесь, как и выше, будем вести речь о г.м.т. в плоскости.
Пусть h и k – различные и не принадлежащие одной прямой лучи (рис. 5).
1.  Откладываем на h и на k отрезки ОН и ОК, равные между собой.
Откладываем на h и на k отрезки ОН и ОК, равные между собой.
2. Проводим через Н и К перпендикуляры к сторонам угла  .
.
3. Отмечаем точку пересечения этих перпендикуляров и обозначаем ее М.
Нетрудно видеть, что 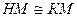 , то есть М равноудалена от сторон угла
, то есть М равноудалена от сторон угла  . Значит исследуемое г.м.т. существует. Обратим еще внимание на то, что точка М лежит внутри
. Значит исследуемое г.м.т. существует. Обратим еще внимание на то, что точка М лежит внутри  .
.
 Легко видеть, что при любом выборе равных между собой отрезков OH i и OК i мы получаем точку M i, равноудаленную от h и k. Все эти точки принадлежат биссектрисе
Легко видеть, что при любом выборе равных между собой отрезков OH i и OК i мы получаем точку M i, равноудаленную от h и k. Все эти точки принадлежат биссектрисе  , которой будет луч ОМ. Таким образом, биссектриса
, которой будет луч ОМ. Таким образом, биссектриса  входит в состав рассматриваемого г.м.т.
входит в состав рассматриваемого г.м.т.
Теперь отметим еще три области (части плоскости), не являющиеся внутренней областью  . Построим лучи m и n, исходящие из О и перпендикулярные соответственно лучам h и k (рис. 6).
. Построим лучи m и n, исходящие из О и перпендикулярные соответственно лучам h и k (рис. 6).
У каждого из трех углов  ,
,  и
и  имеется внутренняя область, их и обозначаем римскими цифрами I, II и III. В областях I и II нет ни одной точки, равноудаленной от сторон
имеется внутренняя область, их и обозначаем римскими цифрами I, II и III. В областях I и II нет ни одной точки, равноудаленной от сторон  . Напротив того, в области III, включая и лучи m и n, каждая точка P i удалена как от луча h так и от луча k на расстояние P i O, то есть P i равноудалена от сторон
. Напротив того, в области III, включая и лучи m и n, каждая точка P i удалена как от луча h так и от луча k на расстояние P i O, то есть P i равноудалена от сторон  .
.
Так же, несложно понять, что и всякая точка, равноудаленная от сторон угла  , либо принадлежит его биссектрисе, ли
, либо принадлежит его биссектрисе, ли



 F 1 следует M
F 1 следует M 
 , параллельная прямой а, а через Ni проводится прямая n, параллельная а.
, параллельная прямой а, а через Ni проводится прямая n, параллельная а.
 Рассмотрим этот пример подробнее. Будем решать вопрос о существовании точек этого г.м.т., разделив плоскость на две части: область, ограниченную окружностью и область, точки которой лежат вне круга, ограниченного окружностью. Так как точки, лежащие в первой области (круге), удалены от окружности (O, R) на расстояние, меньшее R, а точки, лежащие вне круга (O, R), находятся от нее на расстоянии большем R, то следует рассматривать три случая соотношения между h и R: h < R, h = R и h > R.
Рассмотрим этот пример подробнее. Будем решать вопрос о существовании точек этого г.м.т., разделив плоскость на две части: область, ограниченную окружностью и область, точки которой лежат вне круга, ограниченного окружностью. Так как точки, лежащие в первой области (круге), удалены от окружности (O, R) на расстояние, меньшее R, а точки, лежащие вне круга (O, R), находятся от нее на расстоянии большем R, то следует рассматривать три случая соотношения между h и R: h < R, h = R и h > R. . Получаем точку М 1, лежащую внутри круга (O, R) на расстоянии h от окружности.
. Получаем точку М 1, лежащую внутри круга (O, R) на расстоянии h от окружности. . Получаем точку М 2 вне (O, R), которая удалена от окружности на расстояние h.
. Получаем точку М 2 вне (O, R), которая удалена от окружности на расстояние h. , г.м.т. состоит из точки О и окружности (O, R + h).
, г.м.т. состоит из точки О и окружности (O, R + h). Пусть M – произвольная точка m, отличная от О. Тогда из равенства прямоугольных треугольников АОМ и ВОМ следует
Пусть M – произвольная точка m, отличная от О. Тогда из равенства прямоугольных треугольников АОМ и ВОМ следует  , то есть М равноудалена от данных точек А и В.
, то есть М равноудалена от данных точек А и В.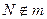 .
. и
и  следует ортогональность прямых ON и AB. В результате
следует ортогональность прямых ON и AB. В результате и
и  . Здесь, как и выше, будем вести речь о г.м.т. в плоскости.
. Здесь, как и выше, будем вести речь о г.м.т. в плоскости. Откладываем на h и на k отрезки ОН и ОК, равные между собой.
Откладываем на h и на k отрезки ОН и ОК, равные между собой.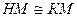 , то есть М равноудалена от сторон угла
, то есть М равноудалена от сторон угла  Легко видеть, что при любом выборе равных между собой отрезков OH i и OК i мы получаем точку M i, равноудаленную от h и k. Все эти точки принадлежат биссектрисе
Легко видеть, что при любом выборе равных между собой отрезков OH i и OК i мы получаем точку M i, равноудаленную от h и k. Все эти точки принадлежат биссектрисе  ,
,  и
и  имеется внутренняя область, их и обозначаем римскими цифрами I, II и III. В областях I и II нет ни одной точки, равноудаленной от сторон
имеется внутренняя область, их и обозначаем римскими цифрами I, II и III. В областях I и II нет ни одной точки, равноудаленной от сторон 


