Проводя такой обзор, мы будем придерживаться Гильбертовской аксиоматики евклидовой геометрии. Поэтому читатель должен ознакомиться с ней, в первую очередь, по книге Д. Гильберта «Основания геометрии». Можно и даже желательно использовать так же и учебное пособие Бахвалова С. В. и Иваницкой В. П. «Основания геометрии», которое базируется на аксиоматике близкой к гильбертовской и содержит значительную систему следствий из нее.
1°. Первые определяемые понятия и некоторые их свойства и отношения между ними.
Первые понятия, содержание которых раскрывается в их определениях, иначе говоря, первые определяемые понятия – это отрезок, луч, полуплоскость. Рассмотрим в основных чертах, как они могут быть определены в рамках евклидовско-гильбертовской схемы.
По Гильберту отрезок  , где A и B – две различные точки – это фигура, состоящая из точек A и B, иначе говоря, пара точек. Однако, сложившейся традиции отвечает представление об отрезке как ограниченной части прямой. В этой трактовке
, где A и B – две различные точки – это фигура, состоящая из точек A и B, иначе говоря, пара точек. Однако, сложившейся традиции отвечает представление об отрезке как ограниченной части прямой. В этой трактовке
отрезок  – это фигура, которой принадлежат точки A и B и каждая точка прямой
– это фигура, которой принадлежат точки A и B и каждая точка прямой  , лежащая между A и B. Естественно, что при этом предполагается и обратное, т. е. каждая точка отрезка – это либо A или B, либо точка, лежащая между A и B.
, лежащая между A и B. Естественно, что при этом предполагается и обратное, т. е. каждая точка отрезка – это либо A или B, либо точка, лежащая между A и B.
Отрезок  в настоящее время принято обозначать –
в настоящее время принято обозначать –  , встречается и несколько иное обозначение –
, встречается и несколько иное обозначение –  , например, в курсе геометрии под редакцией Колмогорова, который являлся основным учебником по геометрии для средней школы в 70-х годах 20 века. Точки A и B называют в этом случае концами отрезка, а точки лежащие между A и B, – его внутренними точками.
, например, в курсе геометрии под редакцией Колмогорова, который являлся основным учебником по геометрии для средней школы в 70-х годах 20 века. Точки A и B называют в этом случае концами отрезка, а точки лежащие между A и B, – его внутренними точками.
Для определения луча обычно вводят понятие «лежать по одну сторону» или «лежать по разные стороны» от фиксированной точки прямой. Итак пусть a – прямая, на которой отмечена точка O (рис. 20).
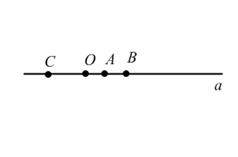
Рис. 20
Будем говорить, что точки A и B, принадлежащие прямой a лежат по разные стороны от её точки O, если O не лежит между точками A и B и при этом отлична от A и В, то есть, если  (O лежит между C и A). Точки
(O лежит между C и A). Точки  и
и  лежат на
лежат на  по одну сторону от
по одну сторону от 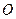 , если
, если 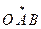 или
или  Здесь сразу приходится рассматривать ряд свойств этих отношений, доказательства которых опустим, используя сами свойства по мере необходимости.
Здесь сразу приходится рассматривать ряд свойств этих отношений, доказательства которых опустим, используя сами свойства по мере необходимости.
Лучом OA с началом в точке O назовем фигуру, которой принадлежат точки O и A и каждая точка прямой OA, лежащая с точкой A по одну сторону от точки O и эта фигура содержит только такие точки.
Луч обозначаем либо двумя буквами O и A, либо одной малой буквой h, и т. п. Если луч обозначен двумя буквами, например, OA и есть опасность другого толкования этого обозначения, то перед обозначением целесообразно написать слово «луч». В упомянутом выше пособии Колмогорова этот недостаток обозначения был снят путем применения скобок: луч OA обозначался [ OA).Точку O луча OA называют началом луча.
Всякая точка O прямой a порождает два луча OA и OB (или h и  ) при
) при  . Такие лучи не имеют ни одной общей точки кроме общего начала
. Такие лучи не имеют ни одной общей точки кроме общего начала 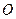 . Их называют взаимно-дополнительными лучами. Если один из лучей целиком принадлежит другому лучу, то их называют сонаправленными или одинаково направленными, а лучи одной прямой имеющие общую часть в виде отрезка или одной точки (начала лучей) называют противоположно направленными. Эти отношения для лучей в дальнейшем обобщаются и распространяются на лучи, лежащие в плоскости, и даже в пространстве, при этом существенно используется понятие параллельности прямых, которое в первой части нашего обзора мы не должны использовать вообще.
. Их называют взаимно-дополнительными лучами. Если один из лучей целиком принадлежит другому лучу, то их называют сонаправленными или одинаково направленными, а лучи одной прямой имеющие общую часть в виде отрезка или одной точки (начала лучей) называют противоположно направленными. Эти отношения для лучей в дальнейшем обобщаются и распространяются на лучи, лежащие в плоскости, и даже в пространстве, при этом существенно используется понятие параллельности прямых, которое в первой части нашего обзора мы не должны использовать вообще.
По аналогии вводится и понятие полуплоскости. Принципиально новым здесь является лишь отношение на множестве точек плоскости, которое характеризует положение пары точек относительно некоторой фиксированной прямой.
Будем говорить, что точки A и B плоскости лежат по одну сторону от прямой  , принадлежащей той же плоскости, если отрезок AB не имеет общих точек с прямой
, принадлежащей той же плоскости, если отрезок AB не имеет общих точек с прямой  (рис. 21 слева).
(рис. 21 слева).


Рис.21
Точки C и D лежат по разные стороны от  , если
, если  и отрезок CD имеют общую внутреннюю точку отрезка CD (рис. 21 справа). Для пары точек P и Q, из которых хотя бы одна принадлежит прямой a, такие отношения не определены (рис. 22).
и отрезок CD имеют общую внутреннюю точку отрезка CD (рис. 21 справа). Для пары точек P и Q, из которых хотя бы одна принадлежит прямой a, такие отношения не определены (рис. 22).

Рис. 22
Полуплоскостью с граничной (или начальной) прямой a называется фигура, которой принадлежит прямая a и каждая точка М плоскости, лежащая по одну сторону с некоторой фиксированной точкой B данной плоскости относительно прямой a (рис. 23).

Рис. 23
Естественно, что и каждая точка полуплоскости – это либо точка прямой  либо точка плоскости, лежащая с B по одну сторону от
либо точка плоскости, лежащая с B по одну сторону от  .
.
Прямая  , подобно точке на какой-либо прямой, делит плоскость на две полуплоскости, которые имеют общими лишь точки их общей граничной прямой
, подобно точке на какой-либо прямой, делит плоскость на две полуплоскости, которые имеют общими лишь точки их общей граничной прямой  . Такие полуплоскости называют противоположными или взаимно дополнительными.
. Такие полуплоскости называют противоположными или взаимно дополнительными.
Пара лучей, имеющих общее начало, называется углом. По поводу этого понятия следует сразу заметить, что в математической литературе можно найти весьма разнообразные его толкования, что связано с различными ситуациями, в которых это понятие используется. Эта разница может носить характер обобщений, а может и представлять собой просто различные понятия по существу, хотя и связанные между собой. Более подробно о понятии угла мы поговорим позже.
Угол, как пара лучей h и k, часто обозначается в виде символа  Для обозначения угла используются и другие обозначения, которые появятся у нас по мере необходимости. Лучи h и k угла
Для обозначения угла используются и другие обозначения, которые появятся у нас по мере необходимости. Лучи h и k угла  называют сторонами угла. А их общее начало – вершиной угла.
называют сторонами угла. А их общее начало – вершиной угла.
Могут иметь место два крайних случая взаимного расположения сторон угла  , которые приводят к понятиям развернутого и нулевого угла: если h и k – взаимно дополнительные лучи, то угол
, которые приводят к понятиям развернутого и нулевого угла: если h и k – взаимно дополнительные лучи, то угол  – развернутый, если h и k совпадают, то
– развернутый, если h и k совпадают, то  – нулевой. Следует заметить, что последний случай – чистая формализация, отражающая естественную потребность в обобщении.
– нулевой. Следует заметить, что последний случай – чистая формализация, отражающая естественную потребность в обобщении.
С углом связывают понятия его внутренней и внешней области. Если  неразвернутый и ненулевой, то с каждой его стороной можно связать полуплоскость: со стороной h – ту, началом которой является прямая, содержащая h, и точки которой лежат по ту же сторону от этой прямой, что и точки луча k (рис. 24); со стороной k – ту, началом которой является прямая, содержащая k, и точки которой лежат по ту же сторону от этой прямой, что и точки луча h (рис. 24).
неразвернутый и ненулевой, то с каждой его стороной можно связать полуплоскость: со стороной h – ту, началом которой является прямая, содержащая h, и точки которой лежат по ту же сторону от этой прямой, что и точки луча k (рис. 24); со стороной k – ту, началом которой является прямая, содержащая k, и точки которой лежат по ту же сторону от этой прямой, что и точки луча h (рис. 24).
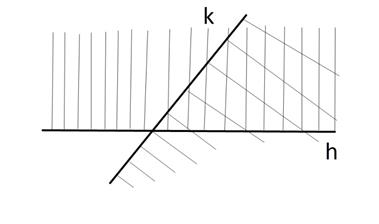
Рис. 24
Эти две плоскости пересекаются (см рис. 24). Полученное пересечение полуплоскостей, за вычетом самих лучей h и k, и называется внутренней областью угла  . Дополнительную к ней часть плоскости (без учета точек лучей h и k) называют внешней областью
. Дополнительную к ней часть плоскости (без учета точек лучей h и k) называют внешней областью  .
.
Для развернутого угла  , строго говоря, внутренняя область не определена (а значит и внешняя). В связи с чем при необходимости любая из полуплоскостей, началом которых является прямая, содержащая лучи h и
, строго говоря, внутренняя область не определена (а значит и внешняя). В связи с чем при необходимости любая из полуплоскостей, началом которых является прямая, содержащая лучи h и  , может быть признана за внутреннюю область
, может быть признана за внутреннюю область  . У нулевого угла
. У нулевого угла 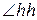 внутренняя область вообще отсутствует (рис. 25).
внутренняя область вообще отсутствует (рис. 25).
Рис. 25
Рассмотрим теперь углы  и
и  , т. е. такие у которых одна пара сторон составляет прямую – это лучи h и
, т. е. такие у которых одна пара сторон составляет прямую – это лучи h и  ,а вторая сторона каждого угла – один и тот же луч k (рис. 26). Такие углы называют смежными.
,а вторая сторона каждого угла – один и тот же луч k (рис. 26). Такие углы называют смежными.

Рис. 26
Если при этом  , то угол
, то угол  (как и угол
(как и угол  ) называют прямым.
) называют прямым.
Если прямые a и b пересекаются в точке O и при этом углы  и
и  , где
, где  , h и
, h и  принадлежат b, являются прямыми, то прямая a называется перпендикулярной к прямой b. (рис. 27)
принадлежат b, являются прямыми, то прямая a называется перпендикулярной к прямой b. (рис. 27)

Рис. 27
Аналогичные понятия можно ввести и в пространстве: понятия двугранного угла, внутренней и внешней области двугранного угла, смежных двугранных углов, прямого двугранного угла. Принципиально новым здесь будет понятие линейного угла двугранного угла.
Пусть мы имеем двугранный угол  с ребром a, т. е. пару полуплоскостей
с ребром a, т. е. пару полуплоскостей  и
и  с общей граничной прямой a. (рис. 28).
с общей граничной прямой a. (рис. 28).

Рис. 28
Возьмем на a произвольную точку А и пусть лучи h и k с началом в точке А принадлежат полуплоскостям  и
и  соответственно, причем
соответственно, причем  и
и 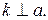 Тогда
Тогда  называют линейным углом двугранного угла
называют линейным углом двугранного угла  .
.
Все линейные углы двугранного угла равны (конгруэнтны) между собой. В этом смысле мы можем считать, что линейный угол однозначно связан с двугранным, а потому может быть принят за определяющий его представитель. В самом деле всякий  однозначно определяет двугранный угол, для которого
однозначно определяет двугранный угол, для которого  будет его линейным углом. Подробное рассмотрение этого вопроса предлагается читателю для самостоятельной работы.
будет его линейным углом. Подробное рассмотрение этого вопроса предлагается читателю для самостоятельной работы.
Вернемся к планиметрии, т. е. к плоским углам  . Важным вопросом является вопрос о существовании прямого угла и вопрос о их равенстве (или неравенстве).
. Важным вопросом является вопрос о существовании прямого угла и вопрос о их равенстве (или неравенстве).
Прежде обратим внимание на то, что на множестве углов плоскости можно определить отношение порядка, которое как обычно мы характеризуем термином «меньше» или «больше»:  меньше
меньше 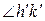 , если
, если  , конгруэнтный
, конгруэнтный 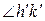 , у которого k
, у которого k  лежит от прямой, содержащей h, по одну сторону с k (рис. 29), таков, что сторона k угла
лежит от прямой, содержащей h, по одну сторону с k (рис. 29), таков, что сторона k угла  принадлежит внутренней области
принадлежит внутренней области  .
.

Рис. 29
В этом случае говорим так же, что 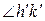 больше
больше  . Нетрудно убедиться в том, что это отношение на множестве углов будет отношением линейного порядка. Для его обозначения используем известный уже знак «<» или «>». Для углов
. Нетрудно убедиться в том, что это отношение на множестве углов будет отношением линейного порядка. Для его обозначения используем известный уже знак «<» или «>». Для углов  и
и 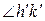 таким образом можно воспользоваться записью
таким образом можно воспользоваться записью  <
< 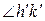 (или
(или 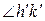 >
>  ).
).
2°. Обратимся теперь к замечательной теореме, теореме о внешнем угле треугольника, которая является как мы сейчас увидим, теоремой абсолютной геометрии. Без этой теоремы мы не можем доказать единственность перпендикуляра к данной прямой, проходящей через наперед заданную точку.
Внешний угол треугольника – это угол смежный с соответствующим ему внутренним углом (рис. 30). Здесь h – это луч ВА, k – это луч ВС.

Рис. 30
Тогда  - смежный с
- смежный с  и
и 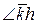 так же смежный с
так же смежный с  .Так как
.Так как 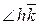 и
и  вертикальные, то они равны.
вертикальные, то они равны.
Теорема 1: Внешний угол треугольника больше любого его внутреннего угла с ним несмежного.
Пусть Е принадлежит дополнительному (противоположному) лучу к лучу АС (рис. 31). Докажем, что  . Допустим, что
. Допустим, что 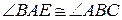 (1).
(1).

Рис. 31
Существует на АЕ точка D такая, что  . Из
. Из  и
и  по аксиоме
по аксиоме  получим
получим  (2).
(2).
Пусть  – смежный углу
– смежный углу  Из допущения (1), равенства (2) и равенства углов, смежных двум равным углам (рис. 32), следует
Из допущения (1), равенства (2) и равенства углов, смежных двум равным углам (рис. 32), следует 

Рис. 32
Но тогда и 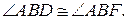 В силу аксиомы
В силу аксиомы  это означает совпадение лучей BF и BD, а значит и принадлежность точки D лучу BF, т. е. прямой BC. Но это означает, что и А принадлежит прямой ВС. Получили противоречие с условием (АВС – треугольник). Таким образом, допущение (1) неверно.
это означает совпадение лучей BF и BD, а значит и принадлежность точки D лучу BF, т. е. прямой BC. Но это означает, что и А принадлежит прямой ВС. Получили противоречие с условием (АВС – треугольник). Таким образом, допущение (1) неверно.
Допустим теперь, что  (рис. 33).
(рис. 33).
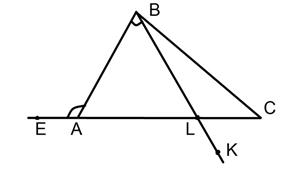
Рис. 33
Тогда существует луч ВК внутри угла  такой, что
такой, что 
 пересекает отрезок АС в точке L (
пересекает отрезок АС в точке L ( ). Относительно
). Относительно 
 внешний, причем по построению
внешний, причем по построению  Но это невозможно согласно первому случаю. Снова полученное противоречие заставляет отбросить и это допущение. Тогда в силу закона трихотомии остается
Но это невозможно согласно первому случаю. Снова полученное противоречие заставляет отбросить и это допущение. Тогда в силу закона трихотомии остается  Точно так же мы можем доказать, что
Точно так же мы можем доказать, что 
Перейдем к вопросу о существовании перпендикуляра к прямой, проходящего через наперед заданную точку.
Теорема 2. Для любой точки В и прямой a существует и притом единственная прямая b, проходящая через В и перпендикулярная к a.
I. Существование
1) Точка В не принадлежит прямой a (рис. 34).

Рис. 34
Возьмем на  точку O. Луч ОВ и один из лучей на прямой a с началом в точке О, который обозначим h, определяют
точку O. Луч ОВ и один из лучей на прямой a с началом в точке О, который обозначим h, определяют  , где k – обозначение луча ОВ. Согласно аксиоме
, где k – обозначение луча ОВ. Согласно аксиоме  со стороны от прямой a, противоположной той, в которой лежит точка В,существует единственный луч
со стороны от прямой a, противоположной той, в которой лежит точка В,существует единственный луч  с началом в точке О такой, что
с началом в точке О такой, что  . На луче
. На луче  существует точка
существует точка  такая, что
такая, что  (акс.
(акс.  ). B и
). B и  – различные точки, так как лежат по разные стороны от a. Существует прямая
– различные точки, так как лежат по разные стороны от a. Существует прямая  (акс. I 1).
(акс. I 1).  и a пересекаются в точке М. Углы
и a пересекаются в точке М. Углы  и
и  смежные. Если О и М различные точки, то из
смежные. Если О и М различные точки, то из  и
и  по аксиоме
по аксиоме 
 . Значит эти углы прямые, т. е.
. Значит эти углы прямые, т. е.  a.
a.
Если же О совпадает с М, то 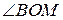 есть угол
есть угол  , где k есть луч МВ;
, где k есть луч МВ;  есть угол
есть угол 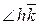 ,где
,где  – луч
– луч  . Но
. Но 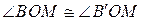 по условию. Значит
по условию. Значит 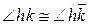 . Это и означает перпендикулярность
. Это и означает перпендикулярность  к a.
к a.
2) В принадлежит  (рис 35).
(рис 35).

Рис. 35
Возьмем С, не принадлежащую  . По доказанному выше существует прямая с, которая проходит через С и перпендикулярна к a. Обозначим луч ОВ через
. По доказанному выше существует прямая с, которая проходит через С и перпендикулярна к a. Обозначим луч ОВ через  , а луч ОС через
, а луч ОС через  . Луч с началом в В, сонаправленный с лучом
. Луч с началом в В, сонаправленный с лучом  , обозначим h. Тогда по аксиоме III 4 существует луч k с началом в В, расположенный от a с той же стороны, что и луч
, обозначим h. Тогда по аксиоме III 4 существует луч k с началом в В, расположенный от a с той же стороны, что и луч  такой что
такой что  . Но всякий угол, конгуэнтный прямому углу, является прямым. Таким образом
. Но всякий угол, конгуэнтный прямому углу, является прямым. Таким образом  – прямой, а прямая, содержащая k перпендикулярна прямой a. Обратим внимание на то, что рассматриваемый случай опирается на утверждение о том, что угол, конгруэнтный прямому углу, является прямым углом.
– прямой, а прямая, содержащая k перпендикулярна прямой a. Обратим внимание на то, что рассматриваемый случай опирается на утверждение о том, что угол, конгруэнтный прямому углу, является прямым углом.
II. Обратимся теперь к вопросу о единственности перпендикуляра к a, проходящего через точку B.
1) Точка В не принадлежит прямой a (рис. 36).

Рис. 36
Допустим, что различные прямые  и
и 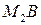 перпендикулярны к a. Тогда имеем
перпендикулярны к a. Тогда имеем  и, например,
и, например, 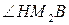 внешний по отношению к
внешний по отношению к  . Здесь H – произвольная точка луча, противоположного лучу
. Здесь H – произвольная точка луча, противоположного лучу  .
.  как углы прямые, но это противоречит теореме о внешнем угле треугольника. Противоречие заставляет отбросить допущение о различии прямых
как углы прямые, но это противоречит теореме о внешнем угле треугольника. Противоречие заставляет отбросить допущение о различии прямых  и
и 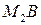 . Таким образом, в этом случае единственность доказана.
. Таким образом, в этом случае единственность доказана.
2) Точка В принадлежит прямой a. Вернемся к рис. 36. СО единственная прямая, проходящая через С и перпендикулярная к a (согласно случаю 1). Но по аксиоме  k единственный луч для которого
k единственный луч для которого  . В силу единственности
. В силу единственности  (
( – луч прямой ОС) луч k, а значит и прямая его содержащая, единственны.
– луч прямой ОС) луч k, а значит и прямая его содержащая, единственны.
Здесь следует обратить внимание на то, что мы фактически использовали то, что любые два прямых угла конгруэнтны (напоминаем, что точка С – произвольная точка).
Для полноты нашего доказательства теоремы 2 следует доказать два утверждения:
1. Все прямые углы конгруэнтны (равны);
2. Угол, конгруэнтный прямому углу, – прямой.
Доказательство утверждения 1 опирается на закон трихотомии, а доказательство утверждения 2 есть следствие равенства углов смежных двум равным углам. Проведем доказательство утверждения 1, а доказательство утверждения 2 оставляем в качестве упражнения читателю.
Итак,  – прямой и
– прямой и 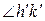 – прямой. Докажем, что
– прямой. Докажем, что  . Пусть
. Пусть  – смежный с
– смежный с  и
и  – смежный с
– смежный с 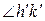 .(рис. 37). Это означает:
.(рис. 37). Это означает:  и
и 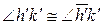 (1).
(1).


Рис. 37
1. Допустим, что  (2) С той же стороны, что и луч k, от прямой, содержащей h, существует согласно аксиоме
(2) С той же стороны, что и луч k, от прямой, содержащей h, существует согласно аксиоме  единственный луч
единственный луч  такой, что
такой, что  . В силу допущения (2)
. В силу допущения (2)  лежит между лучами k и h (внутри угла
лежит между лучами k и h (внутри угла  ). Тогда
). Тогда  (3), как углы смежные равным углам (углам
(3), как углы смежные равным углам (углам  и
и 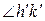 ).
).
Существует прямая, пересекающая лучи k,  и h в точках K,
и h в точках K,  и H. В силу того, что
и H. В силу того, что  лежит между k и h,
лежит между k и h,  . Так как луч k проходит внутри угла
. Так как луч k проходит внутри угла  , то
, то 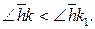 (*). С другой стороны, из (2), (1) и (3) следует, что
(*). С другой стороны, из (2), (1) и (3) следует, что  (**). Как видим, последние два неравенства (*) и (**) противоречат друг другу (в силу закона трихотомии, имеющего место на множестве углов). Полученное противоречие свидетельствует о неверности допущения. Допустив, что
(**). Как видим, последние два неравенства (*) и (**) противоречат друг другу (в силу закона трихотомии, имеющего место на множестве углов). Полученное противоречие свидетельствует о неверности допущения. Допустив, что  мы снова придем к противоречию, что заставляет нас отбросить и это допущение. Тогда в силу трихотомии остается только
мы снова придем к противоречию, что заставляет нас отбросить и это допущение. Тогда в силу трихотомии остается только  . Что и требовалось доказать.
. Что и требовалось доказать.
3  . Теперь перейдем к двум важным соотношениям между сторонами и углами треугольника. Первое устанавливает связь между углами и сторонами одного и того же треугольника, а второе – между сторонами треугольника, так называемое неравенство треугольника.
. Теперь перейдем к двум важным соотношениям между сторонами и углами треугольника. Первое устанавливает связь между углами и сторонами одного и того же треугольника, а второе – между сторонами треугольника, так называемое неравенство треугольника.
Теорема 1: В любом треугольнике АВС против большей стороны лежит больший угол.
Пусть в треугольнике АВС сторона АВ больше АС (рис. 38).

Рис. 38
Тогда на АВ существует точка  такая, что
такая, что  . В этом случае
. В этом случае  равнобедренный и согласно аксиоме
равнобедренный и согласно аксиоме 
 .
.
Луч  принадлежит внутренней области
принадлежит внутренней области  , что является следствием
, что является следствием 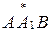 . Это означает в свою очередь:
. Это означает в свою очередь:  . В этом неравенстве
. В этом неравенстве  , можно заменить ему равным
, можно заменить ему равным  , в результате чего получится неравенство
, в результате чего получится неравенство  <
<  .
.
С другой стороны  >
>  , как внешний угол по отношению к
, как внешний угол по отношению к  . Из последних двух неравенств и получаем требуемое:
. Из последних двух неравенств и получаем требуемое:  <
<  .
.
Верно и обратное:против большего угла треугольника лежит большая его сторона.
Это доказывается методом от противного. Если, несмотря на то, что  ,
,  , то по доказанному выше
, то по доказанному выше  . А это противоречит условию.
. А это противоречит условию.
Следствием доказанной теоремы является теорема о перпендикуляре и наклонной, проведенных к одной прямой из одной точки плоскости (рис. 39).

Рис. 39
Здесь 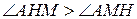 (следствие теоремы о внешнем угле треугольника и определения прямого угла).
(следствие теоремы о внешнем угле треугольника и определения прямого угла).
Теорема 2: Во всяком треугольнике любая сторона меньше суммы двух других сторон.
Для усиления результата докажем, что в 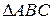 самая большая его сторона меньше суммы двух других.
самая большая его сторона меньше суммы двух других.
Пусть AB – самая большая сторона 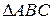 (рис. 40).
(рис. 40).

Рис. 40
Продолжим одну из сторон AС или BC, за точку C, для определенности – 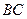 , и на ее продолжении откладываем
, и на ее продолжении откладываем 
 AC. Тогда BC + CA
AC. Тогда BC + CA  BC +
BC +  , Ð
, Ð 
 Ð CB 1 A (как углы равнобедренного треугольника ACB 1).
Ð CB 1 A (как углы равнобедренного треугольника ACB 1).
B 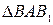 : Ð BAB 1 > Ð CAB 1 (луч AC лежит внутри Ð BAB 1). Значит Ð BAB 1 > Ð CB 1 A. Тогда в силу предыдущей теоремы 1: BB 1 > BA или BC + CB 1 > BA, или BC + CA > BA.
: Ð BAB 1 > Ð CAB 1 (луч AC лежит внутри Ð BAB 1). Значит Ð BAB 1 > Ð CB 1 A. Тогда в силу предыдущей теоремы 1: BB 1 > BA или BC + CB 1 > BA, или BC + CA > BA.
Отметим в заключение приведенного выше обзора некоторых основных фактов евклидовой геометрии, точнее той ее части, которая относится к абсолютной геометрии, критерий принадлежности трех точек одной прямой. Для этого определим сумму отрезков. Для точек A, B и C, принадлежащих одной прямой, AC называем суммой AB и BC, если  . Суммой произвольных отрезков MN и PQ называем отрезок AC, равный сумме отрезков AB и BC, при условиях AB
. Суммой произвольных отрезков MN и PQ называем отрезок AC, равный сумме отрезков AB и BC, при условиях AB  MN, BC
MN, BC  PQ и A, B, C точки одной прямой, для которых
PQ и A, B, C точки одной прямой, для которых  (рис. 41)
(рис. 41)

Рис. 41
Теорема 3: Для произвольных точек A, B и C: AB + BC  AC тогда и только тогда, когда A, B и C принадлежат прямой и
AC тогда и только тогда, когда A, B и C принадлежат прямой и  .
.
1. Если последнее выполнено, то есть A, B и C – на прямой  и
и  , то по определению суммы отрезков AB + BC
, то по определению суммы отрезков AB + BC  AC.
AC.
2. Теперь имеем AB + BC  AC. Если допустить, что A, B и C не принадлежат одной прямой, то в силу предыдущей теоремы 2: AB + BC < AC, что противоречит условию. Это противоречие и означает, что A, B и C принадлежат одной прямой. Тогда
AC. Если допустить, что A, B и C не принадлежат одной прямой, то в силу предыдущей теоремы 2: AB + BC < AC, что противоречит условию. Это противоречие и означает, что A, B и C принадлежат одной прямой. Тогда  есть следствие определения суммы.
есть следствие определения суммы.
4°. Перейдем к обзору основных фактов, связанных с еще одной основной фигурой геометрии Евклида – окружностью.
Под окружностью понимается плоская фигура, или геометрическое место точек плоскости, каждая из которых удалена от некоторой фиксированной точки О на заданное расстояние r. О называют центром окружности, r – ее радиусом.
Встречаются два способа обозначения окружности с центром О и радиуса r: (О, r) и О (r). Второй более старый и в настоящее время практически не встречается. Первый, обозначение в виде пары, по-видимому, более оправдан, поскольку указана (задана) пара, однозначно определяющая рассматриваемую фигуру.
На каждом луче, исходящем из О, существует ровно одна точка, принадлежащая окружности (О, r). Расстояние между любыми двумя точками А и В окружности (О, r) не превосходит 2r (рис. 42).

Рис. 42
Если прямая АВ проходит через О (правая часть рисунка), то АВ  ОА + ОВ
ОА + ОВ  2 r.
2 r.
Если же АВ не проходит через О (левая часть рисунка), то ОАВ – треугольник, а потому AB < OA + OB  2r. Эти два случая обобщаются в одном неравенстве AB ≤ 2r.
2r. Эти два случая обобщаются в одном неравенстве AB ≤ 2r.
Максимальное расстояние между точками окружности, таким образом равно 2r и называется ее диаметром.
Поставим вопрос о существовании общих точек у прямой а и окружности (О, r). Обозначим h расстояние от О до прямой а. Между h и r согласно закону трихотомии, имеющему место на множестве отрезков, возможны три отношения:
1. r < h
2. r  h
h
3. r > h
Рассмотрим их последовательно.
1. r < h. Пусть ОА – отрезок перпендикуляра к а, проходящего через О (рис. 43).

Рис. 43
Согласно определению окружности следует признать, что А не принадлежит (О, r). Для любой точки М i прямой а, отличной от А,  (теорема о наклонной и перпендикуляре), а значит OM i > r, то есть M i не принадлежит (О, r). Таким образом, а и (О, r) не имеют в этом случае ни одной общей точки.
(теорема о наклонной и перпендикуляре), а значит OM i > r, то есть M i не принадлежит (О, r). Таким образом, а и (О, r) не имеют в этом случае ни одной общей точки.
2. r  h. Опустив перпендикуляр из О на а, мы получим: ОА
h. Опустив перпендикуляр из О на а, мы получим: ОА  r, где А – точка пересечения этого перпендикуляра с а (рис. 44).
r, где А – точка пересечения этого перпендикуляра с а (рис. 44).

Рис. 44
Иначе говоря, А принадлежит (О, r). Всякая другая точка M i прямой а удалена от О на расстояние большее ОА, а значит и радиуса окружности. Таким образом, OM i > r.
Вывод: окружность (О, r) и прямая а имеют единственную общую точку А. Заметим, что прямая а в этом случае называется касательной. Говорят: а касается окружности (О, r).
3. r > h. Здесь, в свою очередь, можно выделить как особый случай тот, когда а проходит через О. Как было отмечено выше, на а в этом случае – ровно две точки, принадлежащие (О, r) (см. рис. 42). Будем говорить: прямая а пересекается с (О, r) в двух точках.
Теперь – более общий случай: а не проходит через О. Докажем, что а имеет с (О, r) ровно две общих точки.
Нам потребуется использовать аксиому непрерывности. Выразим понятие непрерывности прямой по Дедекинду (немецкий математик XIX – XX в.в.). Введем понятие сечения отрезка: сечением отрезка АВ будем называть его разбиение на две части К1 и К2, для которых выполняются следующие условия:
1. А принадлежит К1, В принадлежит К2;
2. К1 и К2 имеют точки, отличные от А и В;
3. если М1 принадлежит К1, а М2 – К2, то  2.
2.
Сечение, как обычно, обозначаем в виде пары – (К 1, К 2).
Аксиома непрерывности: Всякое сечение любого отрезка АВ производится некоторой точкой Р в том смысле, что существует на отрезке АВ точка Р такая, что всякая М 1, лежащая между А и Р есть точка К 1, всякая М 2, лежащая между Р и В – точка К 2.
Верно и обратное: любая точка из К 1 есть либо А, либо точка, лежащая между А и Р; всякая точка из К 2 если либо В, либо точка, лежащая между Р и В.
Опустим все первые следствия из аксиомы непрерывности, с некоторыми читатель может познакомиться, например, по «Основаниям геометрии» Бахвалова С.В. и Иваницкой В.П., и обратимся сразу к нашей задаче, задаче о существовании общих точек у прямой и окружности.
Итак, а не проходит через О и ОА < r, где А – точка пересечения а с перпендикуляром к а, проходящим через О. Отложим на а от точки А отрезок АВ  r, например, вправо от А. Так как ОВ > AB (см. теорему о перпендикуляре и наклонной), то ОВ > r. Обозначим К 1 ту часть отрезка АВ, каждая точка которой удалена от О на расстояние меньшее r; К 2 – часть отрезка АВ, каждая точка которой удалена от О на расстояние большее r.
r, например, вправо от А. Так как ОВ > AB (см. теорему о перпендикуляре и наклонной), то ОВ > r. Обозначим К 1 ту часть отрезка АВ, каждая точка которой удалена от О на расстояние меньшее r; К 2 – часть отрезка АВ, каждая точка которой удалена от О на расстояние большее r.
1. Покажем, что К 1 имеет точки, отличные от А.
Пусть на луче ОА отрезок ОС  r (рис. 45).
r (рис. 45).

Рис. 45
Тогда  и потому АС < r. На АВ существует точка М такая, что АМ
и потому АС < r. На АВ существует точка М такая, что АМ  А
А



 , где A и B – две различные точки – это фигура, состоящая из точек A и B, иначе говоря, пара точек. Однако, сложившейся традиции отвечает представление об отрезке как ограниченной части прямой. В этой трактовке
, где A и B – две различные точки – это фигура, состоящая из точек A и B, иначе говоря, пара точек. Однако, сложившейся традиции отвечает представление об отрезке как ограниченной части прямой. В этой трактовке , например, в курсе геометрии под редакцией Колмогорова, который являлся основным учебником по геометрии для средней школы в 70-х годах 20 века. Точки A и B называют в этом случае концами отрезка, а точки лежащие между A и B, – его внутренними точками.
, например, в курсе геометрии под редакцией Колмогорова, который являлся основным учебником по геометрии для средней школы в 70-х годах 20 века. Точки A и B называют в этом случае концами отрезка, а точки лежащие между A и B, – его внутренними точками.
 (O лежит между C и A). Точки
(O лежит между C и A). Точки  и
и  лежат на
лежат на  по одну сторону от
по одну сторону от 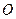 , если
, если 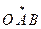 или
или  Здесь сразу приходится рассматривать ряд свойств этих отношений, доказательства которых опустим, используя сами свойства по мере необходимости.
Здесь сразу приходится рассматривать ряд свойств этих отношений, доказательства которых опустим, используя сами свойства по мере необходимости. ) при
) при  . Такие лучи не имеют ни одной общей точки кроме общего начала
. Такие лучи не имеют ни одной общей точки кроме общего начала  , принадлежащей той же плоскости, если отрезок AB не имеет общих точек с прямой
, принадлежащей той же плоскости, если отрезок AB не имеет общих точек с прямой 



 Для обозначения угла используются и другие обозначения, которые появятся у нас по мере необходимости. Лучи h и k угла
Для обозначения угла используются и другие обозначения, которые появятся у нас по мере необходимости. Лучи h и k угла  называют сторонами угла. А их общее начало – вершиной угла.
называют сторонами угла. А их общее начало – вершиной угла.
 , строго говоря, внутренняя область не определена (а значит и внешняя). В связи с чем при необходимости любая из полуплоскостей, началом которых является прямая, содержащая лучи h и
, строго говоря, внутренняя область не определена (а значит и внешняя). В связи с чем при необходимости любая из полуплоскостей, началом которых является прямая, содержащая лучи h и  , может быть признана за внутреннюю область
, может быть признана за внутреннюю область 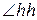 внутренняя область вообще отсутствует (рис. 25).
внутренняя область вообще отсутствует (рис. 25).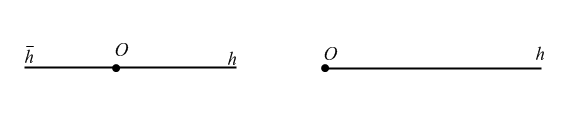
 и
и  , т. е. такие у которых одна пара сторон составляет прямую – это лучи h и
, т. е. такие у которых одна пара сторон составляет прямую – это лучи h и 
 , то угол
, то угол  ) называют прямым.
) называют прямым.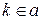 , h и
, h и 
 с ребром a, т. е. пару полуплоскостей
с ребром a, т. е. пару полуплоскостей  и
и  с общей граничной прямой a. (рис. 28).
с общей граничной прямой a. (рис. 28).
 и
и 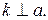 Тогда
Тогда 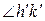 , если
, если  , конгруэнтный
, конгруэнтный  лежит от прямой, содержащей h, по одну сторону с k (рис. 29), таков, что сторона k угла
лежит от прямой, содержащей h, по одну сторону с k (рис. 29), таков, что сторона k угла 

 - смежный с
- смежный с  и
и 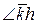 так же смежный с
так же смежный с 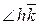 и
и  вертикальные, то они равны.
вертикальные, то они равны. . Допустим, что
. Допустим, что 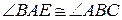 (1).
(1).
 . Из
. Из  и
и  по аксиоме
по аксиоме  получим
получим  (2).
(2). – смежный углу
– смежный углу  Из допущения (1), равенства (2) и равенства углов, смежных двум равным углам (рис. 32), следует
Из допущения (1), равенства (2) и равенства углов, смежных двум равным углам (рис. 32), следует 

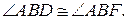 В силу аксиомы
В силу аксиомы  это означает совпадение лучей BF и BD, а значит и принадлежность точки D лучу BF, т. е. прямой BC. Но это означает, что и А принадлежит прямой ВС. Получили противоречие с условием (АВС – треугольник). Таким образом, допущение (1) неверно.
это означает совпадение лучей BF и BD, а значит и принадлежность точки D лучу BF, т. е. прямой BC. Но это означает, что и А принадлежит прямой ВС. Получили противоречие с условием (АВС – треугольник). Таким образом, допущение (1) неверно. (рис. 33).
(рис. 33).

 пересекает отрезок АС в точке L (
пересекает отрезок АС в точке L ( ). Относительно
). Относительно 
 внешний, причем по построению
внешний, причем по построению  Но это невозможно согласно первому случаю. Снова полученное противоречие заставляет отбросить и это допущение. Тогда в силу закона трихотомии остается
Но это невозможно согласно первому случаю. Снова полученное противоречие заставляет отбросить и это допущение. Тогда в силу закона трихотомии остается  Точно так же мы можем доказать, что
Точно так же мы можем доказать, что 

 с началом в точке О такой, что
с началом в точке О такой, что  . На луче
. На луче  существует точка
существует точка  такая, что
такая, что  (акс.
(акс.  ). B и
). B и  (акс. I 1).
(акс. I 1).  и
и  смежные. Если О и М различные точки, то из
смежные. Если О и М различные точки, то из  и
и  по аксиоме
по аксиоме 
 . Значит эти углы прямые, т. е.
. Значит эти углы прямые, т. е.  a.
a.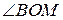 есть угол
есть угол  есть угол
есть угол  – луч
– луч  . Но
. Но 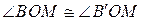 по условию. Значит
по условию. Значит 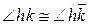 . Это и означает перпендикулярность
. Это и означает перпендикулярность  (рис 35).
(рис 35).
 , а луч ОС через
, а луч ОС через  . Но всякий угол, конгуэнтный прямому углу, является прямым. Таким образом
. Но всякий угол, конгуэнтный прямому углу, является прямым. Таким образом 
 и
и 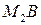 перпендикулярны к a. Тогда имеем
перпендикулярны к a. Тогда имеем  и, например,
и, например, 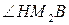 внешний по отношению к
внешний по отношению к  .
.  как углы прямые, но это противоречит теореме о внешнем угле треугольника. Противоречие заставляет отбросить допущение о различии прямых
как углы прямые, но это противоречит теореме о внешнем угле треугольника. Противоречие заставляет отбросить допущение о различии прямых  – смежный с
– смежный с 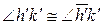 (1).
(1).

 (2) С той же стороны, что и луч k, от прямой, содержащей h, существует согласно аксиоме
(2) С той же стороны, что и луч k, от прямой, содержащей h, существует согласно аксиоме  такой, что
такой, что  . В силу допущения (2)
. В силу допущения (2)  (3), как углы смежные равным углам (углам
(3), как углы смежные равным углам (углам  и H. В силу того, что
и H. В силу того, что  . Так как луч k проходит внутри угла
. Так как луч k проходит внутри угла  , то
, то 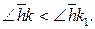 (*). С другой стороны, из (2), (1) и (3) следует, что
(*). С другой стороны, из (2), (1) и (3) следует, что  (**). Как видим, последние два неравенства (*) и (**) противоречат друг другу (в силу закона трихотомии, имеющего место на множестве углов). Полученное противоречие свидетельствует о неверности допущения. Допустив, что
(**). Как видим, последние два неравенства (*) и (**) противоречат друг другу (в силу закона трихотомии, имеющего место на множестве углов). Полученное противоречие свидетельствует о неверности допущения. Допустив, что  мы снова придем к противоречию, что заставляет нас отбросить и это допущение. Тогда в силу трихотомии остается только
мы снова придем к противоречию, что заставляет нас отбросить и это допущение. Тогда в силу трихотомии остается только  . Что и требовалось доказать.
. Что и требовалось доказать. . Теперь перейдем к двум важным соотношениям между сторонами и углами треугольника. Первое устанавливает связь между углами и сторонами одного и того же треугольника, а второе – между сторонами треугольника, так называемое неравенство треугольника.
. Теперь перейдем к двум важным соотношениям между сторонами и углами треугольника. Первое устанавливает связь между углами и сторонами одного и того же треугольника, а второе – между сторонами треугольника, так называемое неравенство треугольника.
 такая, что
такая, что  . В этом случае
. В этом случае  равнобедренный и согласно аксиоме
равнобедренный и согласно аксиоме  .
. принадлежит внутренней области
принадлежит внутренней области  , что является следствием
, что является следствием 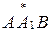 . Это означает в свою очередь:
. Это означает в свою очередь:  . В этом неравенстве
. В этом неравенстве  , можно заменить ему равным
, можно заменить ему равным  , в результате чего получится неравенство
, в результате чего получится неравенство  . Из последних двух неравенств и получаем требуемое:
. Из последних двух неравенств и получаем требуемое:  ,
,  , то по доказанному выше
, то по доказанному выше  . А это противоречит условию.
. А это противоречит условию.
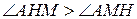 (следствие теоремы о внешнем угле треугольника и определения прямого угла).
(следствие теоремы о внешнем угле треугольника и определения прямого угла).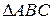 самая большая его сторона меньше суммы двух других.
самая большая его сторона меньше суммы двух других.
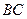 , и на ее продолжении откладываем
, и на ее продолжении откладываем 
 AC. Тогда BC + CA
AC. Тогда BC + CA 
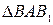 : Ð BAB 1 > Ð CAB 1 (луч AC лежит внутри Ð BAB 1). Значит Ð BAB 1 > Ð CB 1 A. Тогда в силу предыдущей теоремы 1: BB 1 > BA или BC + CB 1 > BA, или BC + CA > BA.
: Ð BAB 1 > Ð CAB 1 (луч AC лежит внутри Ð BAB 1). Значит Ð BAB 1 > Ð CB 1 A. Тогда в силу предыдущей теоремы 1: BB 1 > BA или BC + CB 1 > BA, или BC + CA > BA. . Суммой произвольных отрезков MN и PQ называем отрезок AC, равный сумме отрезков AB и BC, при условиях AB
. Суммой произвольных отрезков MN и PQ называем отрезок AC, равный сумме отрезков AB и BC, при условиях AB  MN, BC
MN, BC 
 , то по определению суммы отрезков AB + BC
, то по определению суммы отрезков AB + BC 

 (теорема о наклонной и перпендикуляре), а значит OM i > r, то есть M i не принадлежит (О, r). Таким образом, а и (О, r) не имеют в этом случае ни одной общей точки.
(теорема о наклонной и перпендикуляре), а значит OM i > r, то есть M i не принадлежит (О, r). Таким образом, а и (О, r) не имеют в этом случае ни одной общей точки.
 2.
2. r, например, вправо от А. Так как ОВ > AB (см. теорему о перпендикуляре и наклонной), то ОВ > r. Обозначим К 1 ту часть отрезка АВ, каждая точка которой удалена от О на расстояние меньшее r; К 2 – часть отрезка АВ, каждая точка которой удалена от О на расстояние большее r.
r, например, вправо от А. Так как ОВ > AB (см. теорему о перпендикуляре и наклонной), то ОВ > r. Обозначим К 1 ту часть отрезка АВ, каждая точка которой удалена от О на расстояние меньшее r; К 2 – часть отрезка АВ, каждая точка которой удалена от О на расстояние большее r.
 и потому АС < r. На АВ существует точка М такая, что АМ
и потому АС < r. На АВ существует точка М такая, что АМ 


