1) Если F(х) первообразная для функции f(х), а G(х) – первообразная для функции g(х), то F(х)+ G(х) первообразная для f(х) +g(х);
2) Если F(х) первообразная для функции f(х) и к- постоянная, то к∙F(х) первообразная для к∙f(х);
3) Если F(х) первообразная для функции f(х) и к,b – постоянные, причём к≠0, то  ∙F(кх+b)- первообразная для f(кх+b).
∙F(кх+b)- первообразная для f(кх+b).
8.4. Понятие интеграла
Обозначение:

(читается: интеграл от а до в эф от икс дэ икс)
Числа а, в, называются пределами интегрирования
8.5. Формула Ньютона – Лейбница:
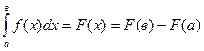
Т.е. для вычисления интеграла необходимо:
1) найти первообразную;
2) подставить в первообразную число в;
3) поставить знак -;
4) подставить в первообразную число а;
5) вычислить.
Функции и графики
А) Линейная функция:
Определение: Линейной функцией называется функция вида у = кх +в
Графиком линейной функции является прямая.
Для построения прямой необходимо две точки:
у=х

Б) Квадратичная функция
Определение: Квадратичной функцией называется функция вида
у = ax² + bx + c
Графиком линейной функции является парабола
Для построения необходимо определить:
1) направление ветвей:
· если а>0, то ветви вверх
· если а<0, то ветви вверх
· 2) вершина (х0, у0): х0 = -  , у0 = у(х0)
, у0 = у(х0)
у=х2

Алгоритм нахождения площади фигуры с помощью интеграла
1. Построить графики функций и найти точки пересечения;
2. Выделить (заштриховать) на чертеже искомую фигуру;
3. Записать формулу вычисления площади;
4. Вычислить значение интегралов.
Случай 1 Случай 2 Случай 3
S= 
| |

2. Примеры и упражнения
Пример 1: Вычислить первообразную
1) f(х)=2х5
F(х)= 
2) f(х)=14х6
F(х)= 
3) f(х)=х4-3х2+6х+7
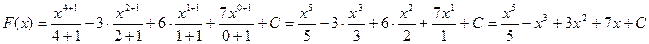 4) f(х)=6х7-13х6+3х2
4) f(х)=6х7-13х6+3х2
 5) f(х)=
5) f(х)=  =34х-10
=34х-10
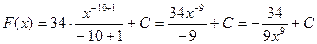
6) f(х)= 

Пример 2: Вычислить интеграл:
1) 
2)

3)

Пример3: Вычислить площадь фигуры, ограниченной линиями
у= 6-х, ось ОХ, х=3,х=5
Решение:
у= 6-х, линейная функция, график – прямая
Получили, что прямая проходит через точки (1;5) (2;4)

Тогда (случай 1):

Ответ: S=4ед2
Пример4: Вычислить площадь фигуры, ограниченной линиями
f(х) = х2-8х+16, f(х)=-х+6
Решение:
1) Построим графики функций, заданных в условии
f(х) = х2-8х+16
График парабола
Для построения:
а)т.к. 1>0, то ветви вверх
в) вершина (х0, у0): х0 = -  =-
=-  ,
,
у0 = у(х0)=у(4)= 42-8·4+16=16-32+16=0, т.е. вершина (4;0)
f(х)= -х+6
График прямая.Для построения:
у(1)= -1+6=5
у(2)= -2+6=4, таким образом получили точки:
(1;5), (2;4)
Строим график:

Случай 3, тогда: 

 S=7,5-3=4,5 ед2
S=7,5-3=4,5 ед2
Ответ: S=4,5 ед2
Варианты контрольной работы
Задание 1: Вычислить первообразную
Вариант 1: f(x) = 3х ³-4х²+15sinх
Вариант 2: f(х) =12х3- 
Вариант 3: f(х) = 12х6-6х5-10х4+4х3-4х2+6
Вариант 4: f(х) = 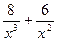
Вариант 5: f(х) = 4sinx –5cosx +ех
Вариант 6: f(х) = 
Вариант 7: f(х) = 
Вариант 8: 
Вариант 9: f(х) = 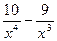
Вариант 10: f(х) = 
Вариант 11: f(х) = 
Вариант 12: f(х) = 
Вариант 13: f(х) = 
Вариант14: f(х) = 4sinx –5cosx +ех
Вариант 15: f(х) = 
Вариант 16: f(х) =4х5-12х4+17х3-15х2+4х-3
Вариант 17: f(х) =14х6-12х5-5х4+8х3-х2+3
Вариант 18: f(х) = 
Вариант1 9: f(х) = 
Вариант 20: f(х) = 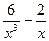
Вариант 21:f(х) = 
Вариант 22: f(х) = 12х6-6х5-10х4+4х3-4х2+6
Вариант 23: f(х) = 2sinx+3cosx - 
Вариант 24: f(х) = 4sinx –5cosx +ех
Вариант 25: f(х) = 
Вариант 26: f(х) =14х5+х4-7х3-х2+4х
Вариант 27: f(х) = 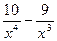
Вариант 28: f(х) = 4sinx –5cosx +ех
Вариант 29: 
Вариант 30 (х) = 14х6-12х5-5х4+8х3-х2+3
Задание 2: Вычислить интеграл
| Вариант 1:
| 
| 
|
| Вариант 2:
| 
| 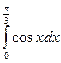
|
| Вариант 3:
| 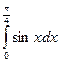
| 
|
| Вариант 4:
| 
| 
|
| Вариант 5:
| 
| 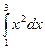
|
| Вариант 6:
| 
| 
|
| Вариант 7:
| 
| 
|
| Вариант 8:
| 
| 
|
| Вариант 9:
| 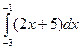
| 
|
| Вариант 10:
| 
| 
|
| Вариант 11:
| 
| 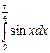
| |
| Вариант 12:
| 
| 
| |
| Вариант 13:
| 
| 
| |
| Вариант 14:
| 
| 
| |
| Вариант 15:
| 
| 
| |
| Вариант 16:
| 
| 
| |
| Вариант 17:
| 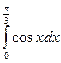
| 
| |
| Вариант 18:
| 
| 
| |
| Вариант 19:
| 
| 
| |
| Вариант 20:
| 
| 
| |
| Вариант 21:
| 
| 
|
| Вариант 22:
| 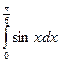
| 
|
| Вариант 23:
| 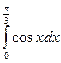
| 
|
| Вариант 24:
| 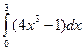
| 
|
| Вариант 25:
| 
| 
|
| Вариант 26:
| 
| 
|
| Вариант 27:
| 
| 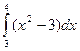
|
| Вариант 28:
| 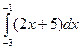
| 
|
| Вариант 29:
| 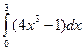
| 
|
| Вариант 30:
| 
| 
|
Задание 3: Вычислить площадь фигуры, ограниченной линиями
Вариант 1: у=х2-8х+18, ось ОХ
Вариант 2: у=6-х, ось ОХ, х=3, х=5
Вариант 3: у=-х2+4х+1, у=х+1
Вариант 4: у=4-х, ось ОХ, х=1, х=3
Вариант 5: у=х2-8х+16, у=6-х
Вариант 6: у=-х2+8х-11, у=х-1
Вариант 7: у=х2-4х+4, у=4-х
Вариант 8: у=2х2-12х+19, ось ОХ
Вариант 9: у = -х+1, ось Ох, ось Оу
Вариант 10: у=-х2+4х-2, у=х2-4х+4
Вариант 11: у =х2, у = -х+2
Вариант 12: у = 1-х2, ось Ох, ось Оу
Вариант 13: у=-х2+6х-7, у=х2-6х+9
Вариант14: у = -х+3, ось Ох, ось Оу
Вариант 15: у =х2, ось Ох, х=0,х=2
Вариант 16: у=х2-8х+17, у=-х2+10х-19
Вариант 17: у = 8-х, ось ОХ, х=5, х=7
Вариант 18: у =х2, ось Ох, х=1,х=9
Вариант1 9: у=-х2+4х+2, у=х2-6х+10
Вариант 20: у = х2-2х+2, у=-х2+4х+2
Вариант 21: у = 16-х, ось ОХ, х=1, х=2
Вариант 22: у = -х2+2х+9, у = 3х2-6х+5
Вариант 23: у =х2, ось Ох, х=1,х=4
Вариант 24: у=х2-4х+4, у=4-х
Вариант 25: у=-х2+4х+2, у=х2-6х+10
Вариант 26: у=х2-8х+16, у=6-х
Вариант 27: у = -х2+2х+9, у = 3х2-6х+5
Вариант 28: у=2х2-12х+19, ось ОХ
Вариант 29: у=х2-8х+18, ось ОХ
Вариант 30: у=-х2+6х-7, у=х2-6х+9
Содержание темы «Элементы теории вероятностей, комбинаторики и математической статистики»

Предмет комбинаторики. Цели и задачи комбинаторики. Общие правила комбинаторики.
Цели и задачи комбинаторики, общие правила, сведения из истории комбинаторики, связь с другими науками. Основные понятия комбинаторики
Основные комбинаторные понятия и формулы.
Определение факториала, сочетаний, размещений, перестановок элементов. Комбинаторные задачи.
Формула бинома Ньютона.
Формула Ньютона и основные следствия. Свойства биноминальных коэффициентов. Треугольник Паскаля
Событие, вероятность события, сложение и умножение вероятностей
Классическое и статистическое определения вероятности;
теоремы сложения и умножения вероятностей; формула полной вероятности;
Дискретная случайная величина, закон ее распределения. Числовые характеристики дискретной случайной величины
Понятие дискретной случайной величины и закон ее распределения;числовые характеристики дискретной случайной величины.
Представление данных (таблицы, диаграммы, графики).
Разные виды диаграмм, использование диаграмм, таблиц, графиков
Генеральная совокупность, выборка, среднее арифметическое, медиана.
Среднее значение (среднее арифметическое) набора;наибольшее и наименьшее значения набора чисел, его размах;отклонения от среднего арифметического и дисперсия;
Основные сведения из теории
9.1. Определение вероятности
Теория вероятностей занимается исследованием вероятностных закономерностей массовых однородных явлений, многие её практические приложения используются в математической статистике.
Определение: Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:
 - классическое определение вероятности.
- классическое определение вероятности.
9.2. Основные формулы комбинаторики
При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества.
Перестановки
Определение Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения.
Число всех возможных перестановок:
Рп = п! (n факториал)
п!=1∙2∙3∙4∙…….∙n
Размещения
Определение: Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком.
Число всех возможных размещений
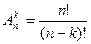
Сочетания
Определение: Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов).
Число сочетаний

9.3. Формула Бернулли
 ., где
., где
n – число опытов А;
к – число наступления события А;
р- вероятность события А;
q – вероятность не наступления события А (q=1-р);
9.4. Определения теории математической статистики
Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.
Определение: Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения – соответствующими малыми буквами (xi, yi,…).
Случайные величины подразделяются на две группы: дискретные и непрерывные.
Определение: Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Определение: Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.



 ∙F(кх+b)- первообразная для f(кх+b).
∙F(кх+b)- первообразная для f(кх+b).
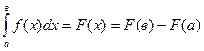

 , у0 = у(х0)
, у0 = у(х0)




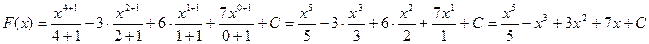 4) f(х)=6х7-13х6+3х2
4) f(х)=6х7-13х6+3х2 5) f(х)=
5) f(х)=  =34х-10
=34х-10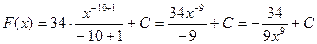







 ,
,


 S=7,5-3=4,5 ед2
S=7,5-3=4,5 ед2
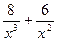


















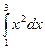





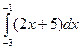



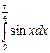
















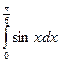


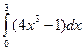




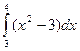



 - классическое определение вероятности.
- классическое определение вероятности.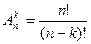

 ., где
., где

