1. Найти производную 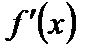 .
.
2. Найти критические точки, т.е. точки, в которых 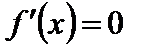 или производная не существует.
или производная не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов.
4. Найти экстремальные значения функции.
Пример. Исследовать на экстремум функцию 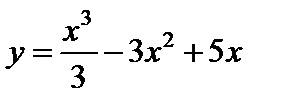 .
.
Решение:
1) 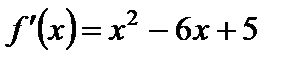 ;
;
2) 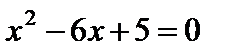 ,
, 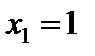 ,
, 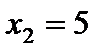 ;
;
3) применяя метод интервалов, находим, что 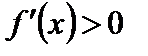 на
на 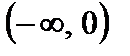 и на
и на 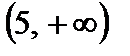 , а неравенство
, а неравенство 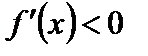 выполняется на
выполняется на 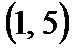 .
.
Следовательно, в точке 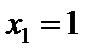 имеется максимум, а в точке
имеется максимум, а в точке 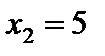 – минимум;
– минимум;
4) находим 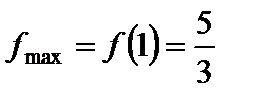 ,
, 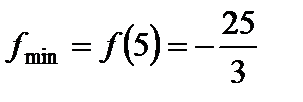 .
.
Исследование функции с помощью
второй производной
Будем рассматривать дважды дифференцируемую функцию, т.е. функцию 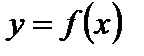 , которая имеет производные
, которая имеет производные 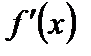 и
и 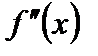 .
.
Второе достаточное условие экстремума. Если в точке 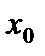 первая производная равна нулю:
первая производная равна нулю: 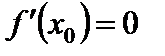 , а вторая положительна:
, а вторая положительна: 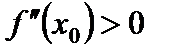 , то
, то 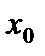 есть точка минимума функции
есть точка минимума функции 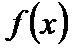 ; если же
; если же 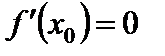 ,
, 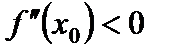 , то
, то 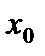 – точка максимума.
– точка максимума.
Доказательство. Пусть 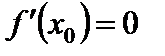 ,
, 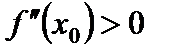 . Тогда, так как
. Тогда, так как 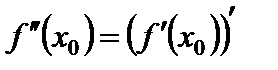 , первая производная возрастает в окрестности точки
, первая производная возрастает в окрестности точки 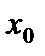 . Значит, слева от
. Значит, слева от 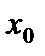 она отрицательна:
она отрицательна: 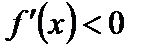 , а справа – положительна:
, а справа – положительна: 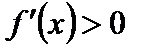 . Итак, при переходе через
. Итак, при переходе через 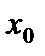 производная меняет знак с минуса на плюс. Следовательно, в этой точке минимум. Аналогично рассматривается случай
производная меняет знак с минуса на плюс. Следовательно, в этой точке минимум. Аналогично рассматривается случай 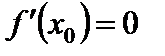 ,
, 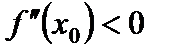 .
.
Пример. 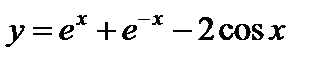 .
. 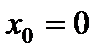 .
.
Имеем:
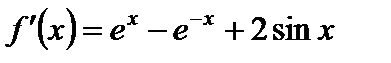 ,
, 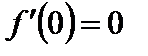
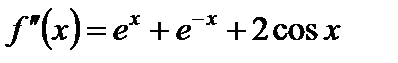 ,
, 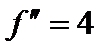 ;
; 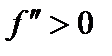 .
.
Следовательно, в точке 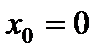 имеется минимум.
имеется минимум.
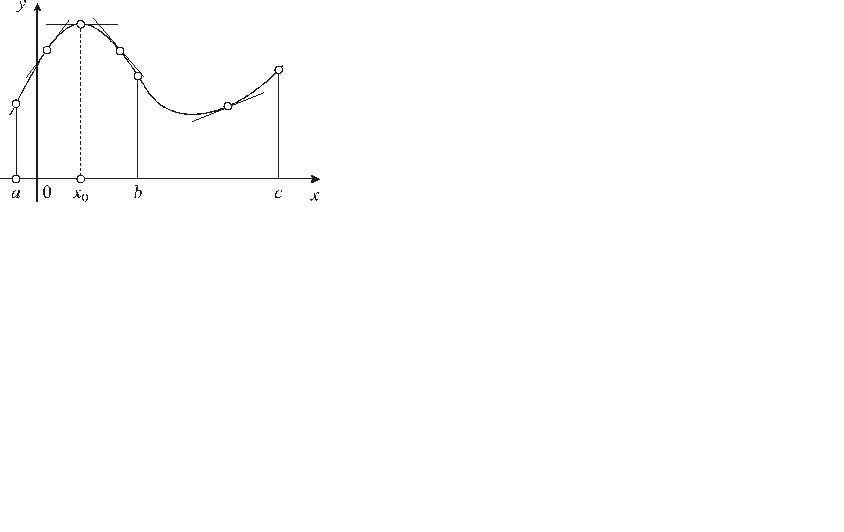
Функция и ее график характеризуются также направлением выпуклости и наличием асимптот. Говорят, что на данном интервале выпуклость графика направлена вверх (вниз), если все его точки находятся ниже (соответственно выше) любой касательной на этом интервале.
На рис. 2 показан график функции, у которого на интервале 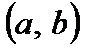 выпуклость направлена вверх, а на интервале
выпуклость направлена вверх, а на интервале 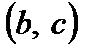 – вниз.
– вниз.
Точка, в которой меняется направление выпуклости, называется точкой перегиба.
|
| Рис. 2
|
Можно доказать, что если на данном интервале 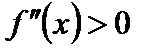 , то выпуклость графика направлена вниз, если же
, то выпуклость графика направлена вниз, если же 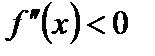 , то выпуклость направлена вверх.
, то выпуклость направлена вверх.
Если 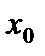 – точка перегиба, то
– точка перегиба, то 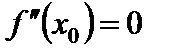 .
.
Асимптоты
Определение. Асимптотой графика функции 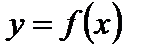 называется прямая, обладающая тем свойством, что расстояние от переменной точки М графика до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат.
называется прямая, обладающая тем свойством, что расстояние от переменной точки М графика до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат.
Различают вертикальные и наклонные асимптоты. Прямая 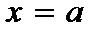 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если 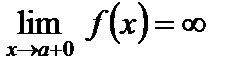 или
или 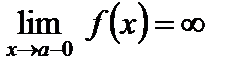 . Вертикальные асимптоты сопутствуют обычно точкам разрыва второго рода.
. Вертикальные асимптоты сопутствуют обычно точкам разрыва второго рода.
Из школьного курса известно, в частности, что ось Oy (т.е. прямая  ) есть вертикальная асимптота графика функции
) есть вертикальная асимптота графика функции 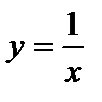 .
.
Прямая 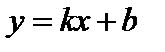 есть наклонная асимптота графика функции
есть наклонная асимптота графика функции 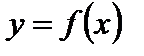 при
при 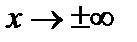 , если
, если
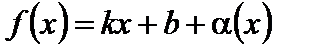 ,
,
где 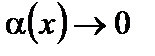 при
при 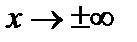 .
.
Коэффициенты k и b в уравнении наклонной асимптоты находят по формулам:
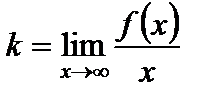 ,
,
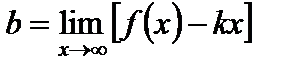 .
.
Пример. Найти наклонную асимптоту графика функции 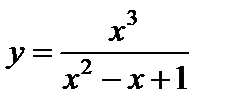 .
.
Решение.
1) 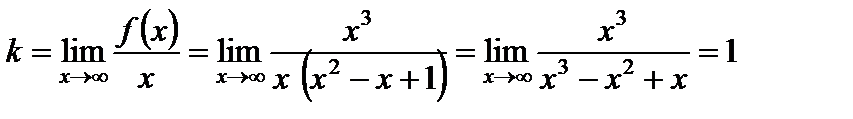 ;
;
2) 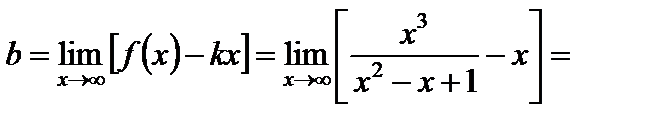
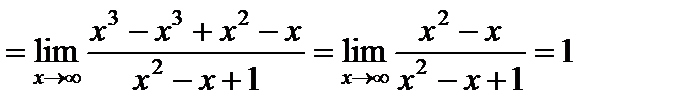 .
.
Уравнение асимптоты: 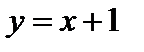 .
.
Заметим, что наличие у функции 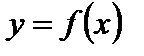 наклонной асимптоты
наклонной асимптоты 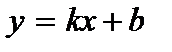 означает, что при больших значениях аргумента функция мало отличается от линейной функции.
означает, что при больших значениях аргумента функция мало отличается от линейной функции.
Общая схема исследования функций
и построения их графиков
Для исследования функции и построения графика следует найти:
1) область определения функции;
2) точки разрыва функции;
3) интервалы возрастания и убывания функции;
4) максимумы и минимумы;
5) направление выпуклости графика функции, точки перегиба;
6) асимптоты.
Кроме того, учитываются четность (или нечетность) функции, периодичность, точки пересечения графика с осями координат.
На основании проведенного исследования строится график функции, при этом полезно намечать элементы графика параллельно с исследованием.
Пример 1. Исследовать функцию 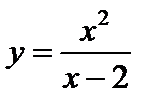 и построить ее график.
и построить ее график.
1. Область определения – вся числовая прямая за исключением точки 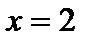 , т.е. множество
, т.е. множество
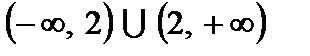 .
.
2. 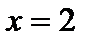 – точка разрыва 2-го рода, так как
– точка разрыва 2-го рода, так как
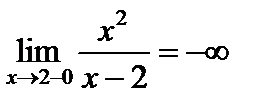 ,
, 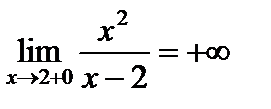 .
.
3. Вычислим производную:
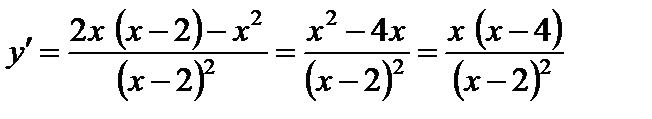 .
.
Определим области возрастания и убывания функции:
при 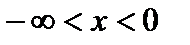 имеем
имеем 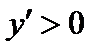 – функция возрастает;
– функция возрастает;
при 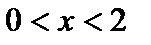 и
и 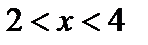 имеем
имеем 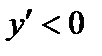 – функция убывает;
– функция убывает;
при 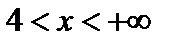 имеем
имеем 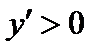 – функция возрастает.
– функция возрастает.
4. Из равенства 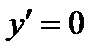 находим критические точки
находим критические точки 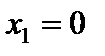 ,
, 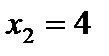 . В точке
. В точке 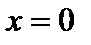 производная меняет знак с плюса на минус
производная меняет знак с плюса на минус 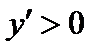 при
при 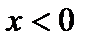 ;
; 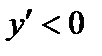 при
при 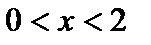 ). Следовательно, в точке
). Следовательно, в точке 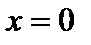 имеется максимум:
имеется максимум:
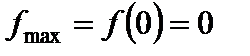 .
.
В точке 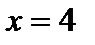 производная меняет знак с минуса на плюс (
производная меняет знак с минуса на плюс (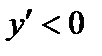 при
при 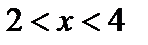 ,
, 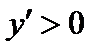 при
при 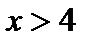 ). Следовательно, в точке
). Следовательно, в точке 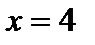 имеется максимум:
имеется максимум:
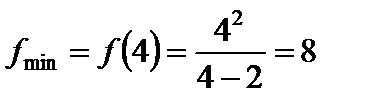 .
.
5. Вычислим вторую производную:
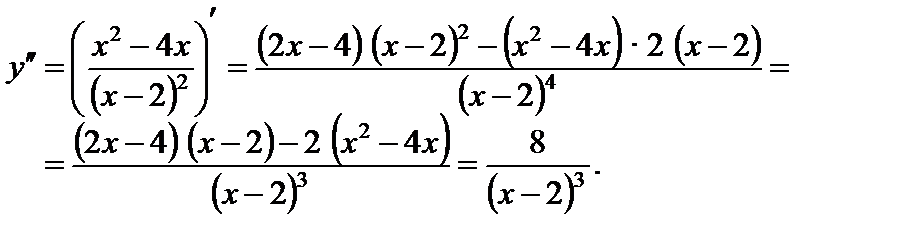
Определим направление выпуклости:
при 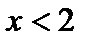 имеем
имеем 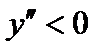 – выпуклость направлена вверх,
– выпуклость направлена вверх,
при 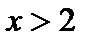 имеем
имеем 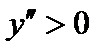 – выпуклость направлена вниз.
– выпуклость направлена вниз.
Точек перегиба нет.
Определим асимптоты графика.
Очевидно, 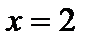 – вертикальная асимптота.
– вертикальная асимптота.
Определим наклонную асимптоту.
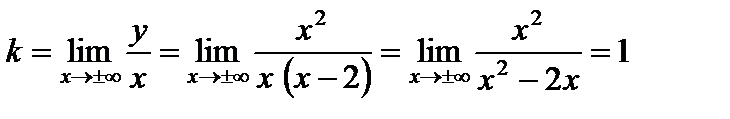 ,
,
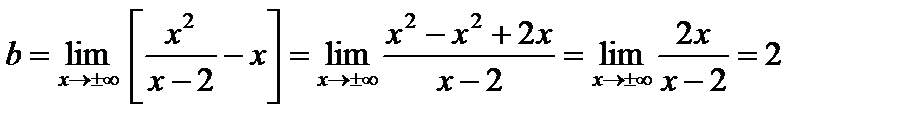 .
.
Итак, 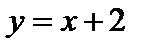 – наклонная асимптота.
– наклонная асимптота.
График исследуемой функции изображен на рис. 3.
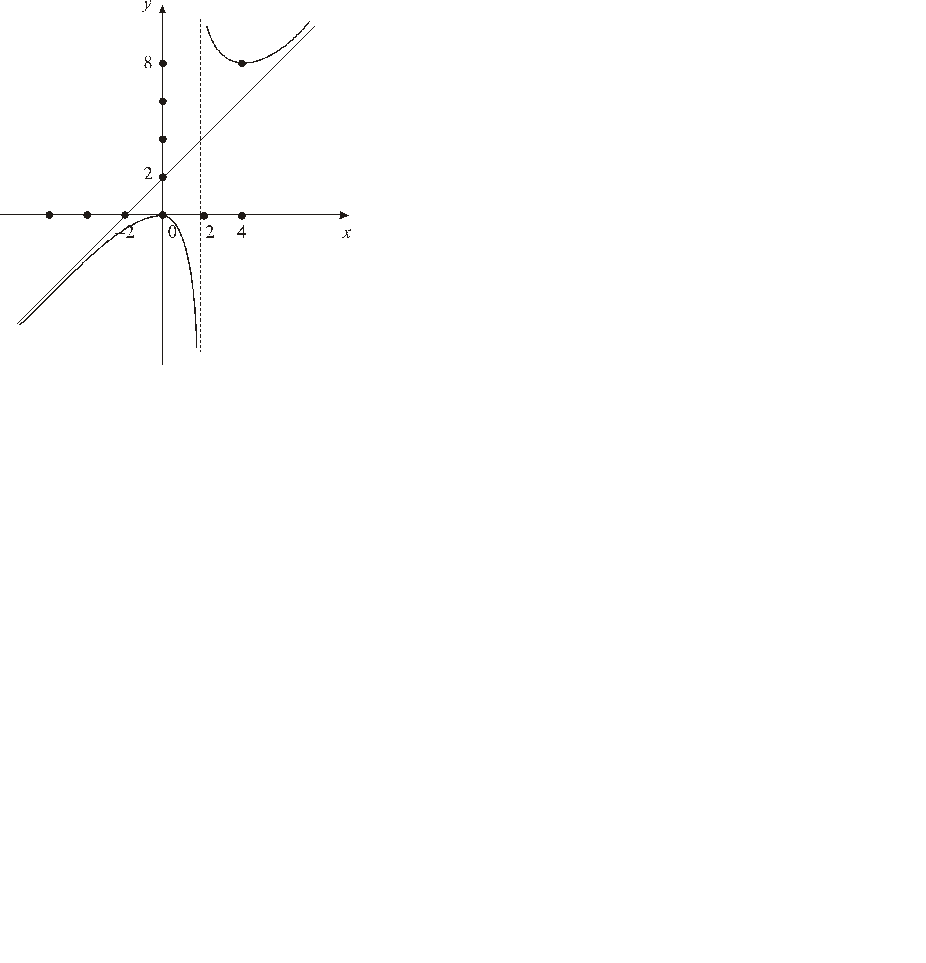
|
| Рис. 3
|
Пример 2. В теории вероятностей и в статистике весьма важную роль играет функция
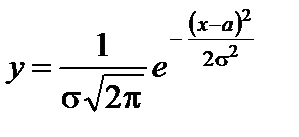
– дифференциальная функция нормального распределения. Исследуем эту функцию методами дифференциального исчисления по приведенной выше схеме и построим ее график. Заметим, что этот график называют нормальной кривой (кривой Гаусса).
Решение. 1. Область определения функции – вся ось Ox.
2. Функция непрерывна на всей оси Ox.
3. Вычислим первую производную:
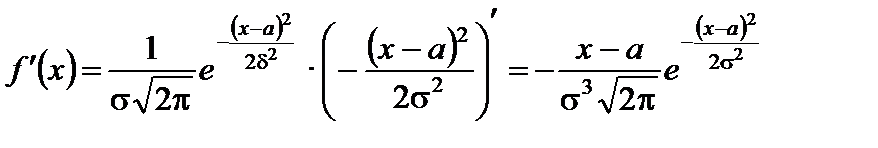 .
.
Легко видеть, что 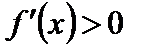 при
при  ,
, 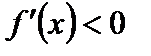 при
при  . Следовательно, на интервале
. Следовательно, на интервале 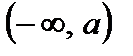 функция возрастает, а на интервале
функция возрастает, а на интервале 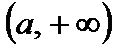 – убывает.
– убывает.
4. Приравнивая производную к нулю, находим критическую точку 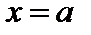 . В точке
. В точке 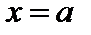 производная меняет знак с плюса на минус, следовательно, в ней имеется максимум:
производная меняет знак с плюса на минус, следовательно, в ней имеется максимум:
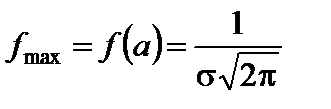 .
.
5. Вычисляем вторую производную:
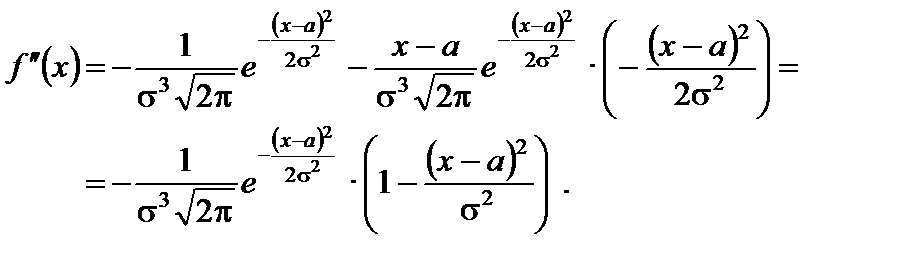
Легко видеть, что вторая производная равна нулю, когда
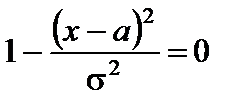 , т.е. при
, т.е. при 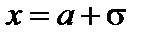 и
и 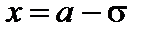 .
.
Имеем
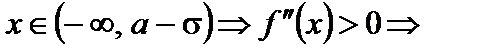 выпуклость направлена вниз
выпуклость направлена вниз
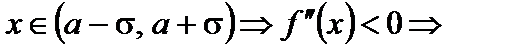 выпуклость направлена вверх
выпуклость направлена вверх
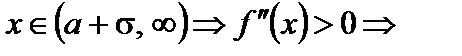 выпуклость направлена вниз.
выпуклость направлена вниз.
При переходе через точки 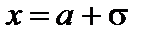 ,
, 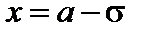 вторая производная меняет знак. Значение функции в обеих этих точках одно и то же:
вторая производная меняет знак. Значение функции в обеих этих точках одно и то же:
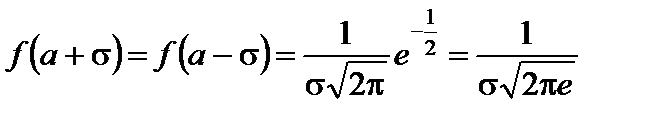 .
.
Таким образом, точками перегиба графика являются точки
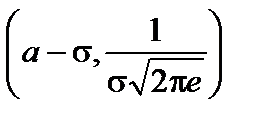 и
и 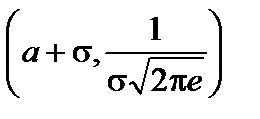 .
.
6. Вертикальных асимптот, очевидно, нет. Предел функции при 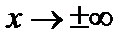 равен нулю:
равен нулю: 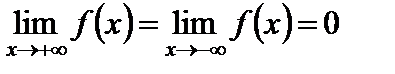 .
.
Следовательно, ось Ox есть горизонтальная асимптота графика (очевидно, 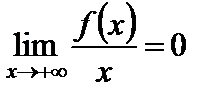 , и наклонных асимптот нет).
, и наклонных асимптот нет).
При построении графика учтем дополнительно, что при всех значениях аргумента 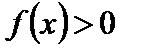 , т.е. кривая расположена выше оси Ox, а также тот факт, что кривая симметрична относительно прямой
, т.е. кривая расположена выше оси Ox, а также тот факт, что кривая симметрична относительно прямой 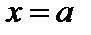 (так как разность
(так как разность 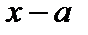 содержится в аналитическом выражении функции в квадрате).
содержится в аналитическом выражении функции в квадрате).
Возьмем для определенности 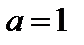 ,
, 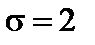 .
.

Рис. 4



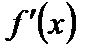 .
.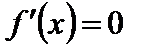 или производная не существует.
или производная не существует.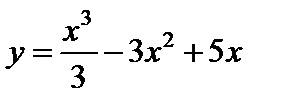 .
.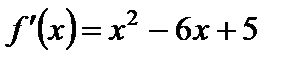 ;
;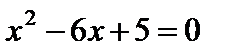 ,
, 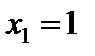 ,
, 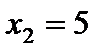 ;
;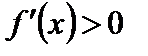 на
на 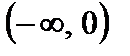 и на
и на 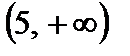 , а неравенство
, а неравенство 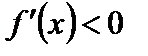 выполняется на
выполняется на 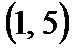 .
.
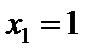 имеется максимум, а в точке
имеется максимум, а в точке 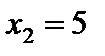 – минимум;
– минимум;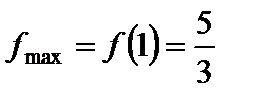 ,
, 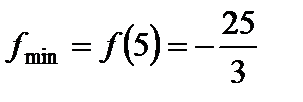 .
.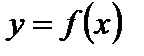 , которая имеет производные
, которая имеет производные 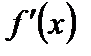 и
и 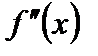 .
.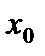 первая производная равна нулю:
первая производная равна нулю: 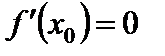 , а вторая положительна:
, а вторая положительна: 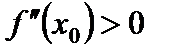 , то
, то 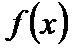 ; если же
; если же 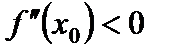 , то
, то 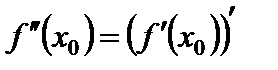 , первая производная возрастает в окрестности точки
, первая производная возрастает в окрестности точки 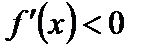 , а справа – положительна:
, а справа – положительна: 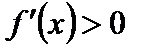 . Итак, при переходе через
. Итак, при переходе через 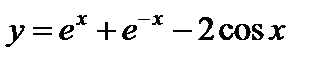 .
. 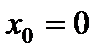 .
.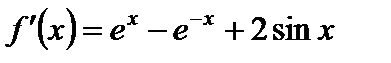 ,
, 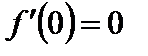
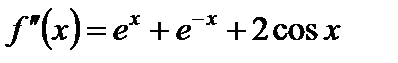 ,
, 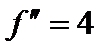 ;
; 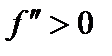 .
.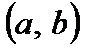 выпуклость направлена вверх, а на интервале
выпуклость направлена вверх, а на интервале 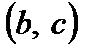 – вниз.
– вниз.
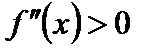 , то выпуклость графика направлена вниз, если же
, то выпуклость графика направлена вниз, если же 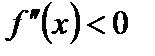 , то выпуклость направлена вверх.
, то выпуклость направлена вверх.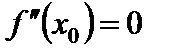 .
.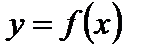 называется прямая, обладающая тем свойством, что расстояние от переменной точки М графика до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат.
называется прямая, обладающая тем свойством, что расстояние от переменной точки М графика до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат.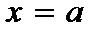 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если 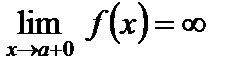 или
или 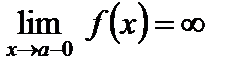 . Вертикальные асимптоты сопутствуют обычно точкам разрыва второго рода.
. Вертикальные асимптоты сопутствуют обычно точкам разрыва второго рода. ) есть вертикальная асимптота графика функции
) есть вертикальная асимптота графика функции 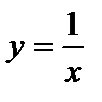 .
.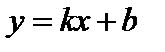 есть наклонная асимптота графика функции
есть наклонная асимптота графика функции 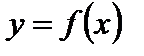 при
при 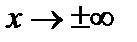 , если
, если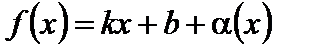 ,
,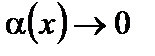 при
при 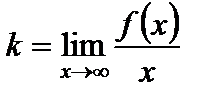 ,
,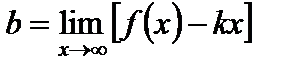 .
.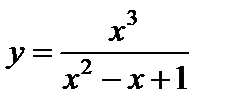 .
.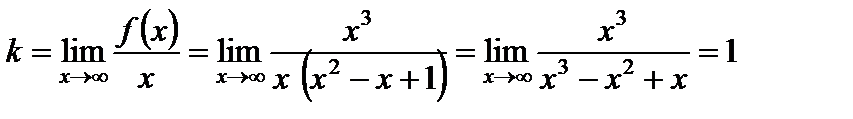 ;
;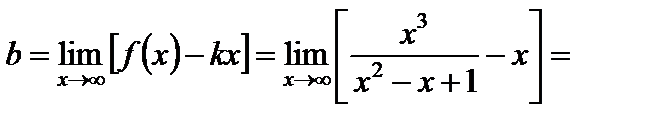
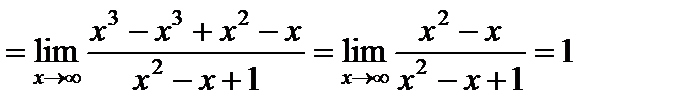 .
.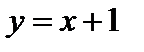 .
.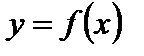 наклонной асимптоты
наклонной асимптоты 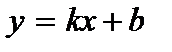 означает, что при больших значениях аргумента функция мало отличается от линейной функции.
означает, что при больших значениях аргумента функция мало отличается от линейной функции.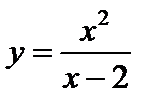 и построить ее график.
и построить ее график.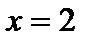 , т.е. множество
, т.е. множество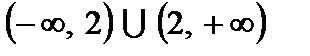 .
.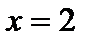 – точка разрыва 2-го рода, так как
– точка разрыва 2-го рода, так как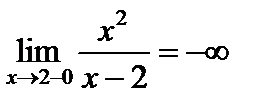 ,
, 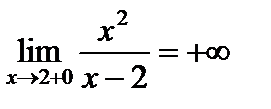 .
.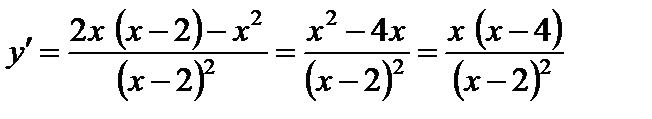 .
.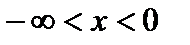 имеем
имеем 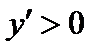 – функция возрастает;
– функция возрастает;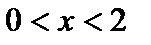 и
и 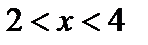 имеем
имеем 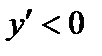 – функция убывает;
– функция убывает;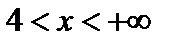 имеем
имеем 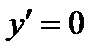 находим критические точки
находим критические точки 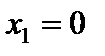 ,
, 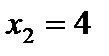 . В точке
. В точке 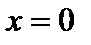 производная меняет знак с плюса на минус
производная меняет знак с плюса на минус 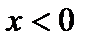 ;
; 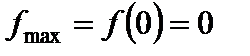 .
.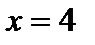 производная меняет знак с минуса на плюс (
производная меняет знак с минуса на плюс (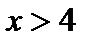 ). Следовательно, в точке
). Следовательно, в точке 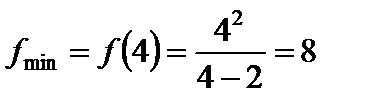 .
.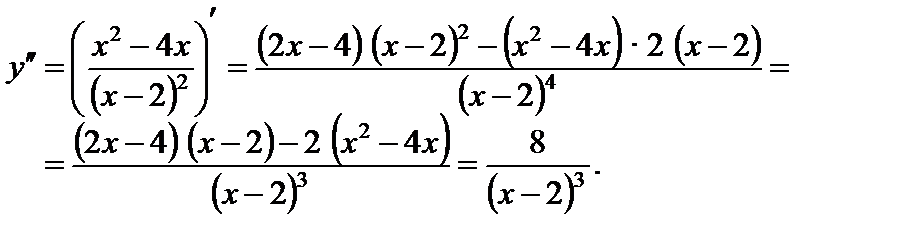
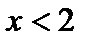 имеем
имеем 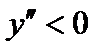 – выпуклость направлена вверх,
– выпуклость направлена вверх,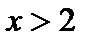 имеем
имеем 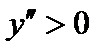 – выпуклость направлена вниз.
– выпуклость направлена вниз.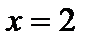 – вертикальная асимптота.
– вертикальная асимптота.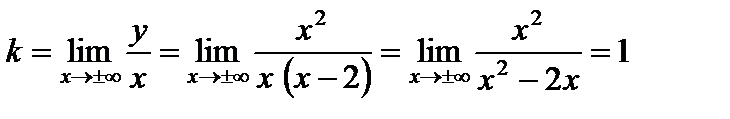 ,
,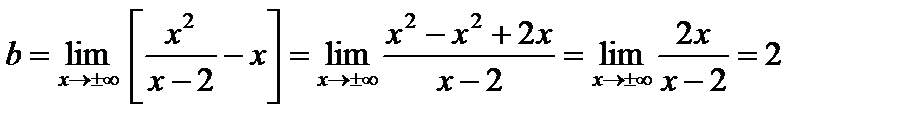 .
.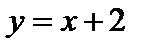 – наклонная асимптота.
– наклонная асимптота.
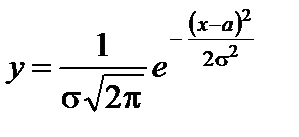
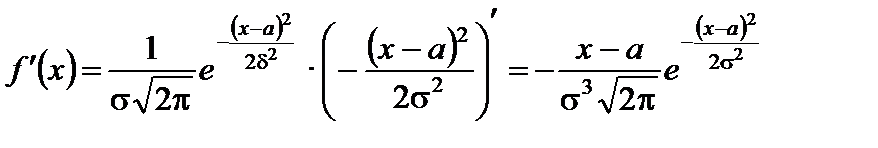 .
.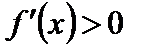 при
при  ,
, 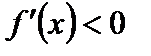 при
при  . Следовательно, на интервале
. Следовательно, на интервале 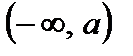 функция возрастает, а на интервале
функция возрастает, а на интервале 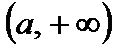 – убывает.
– убывает.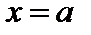 . В точке
. В точке 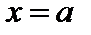 производная меняет знак с плюса на минус, следовательно, в ней имеется максимум:
производная меняет знак с плюса на минус, следовательно, в ней имеется максимум: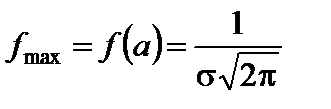 .
.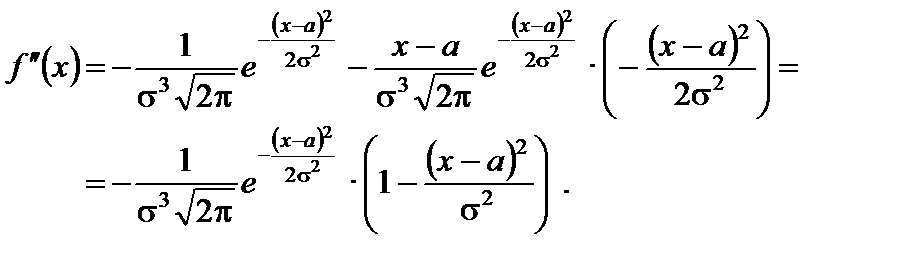
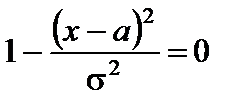 , т.е. при
, т.е. при 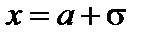 и
и 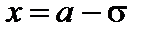 .
.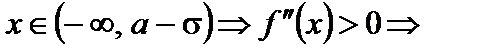 выпуклость направлена вниз
выпуклость направлена вниз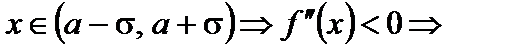 выпуклость направлена вверх
выпуклость направлена вверх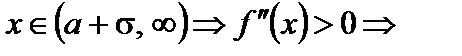 выпуклость направлена вниз.
выпуклость направлена вниз.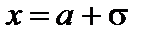 ,
, 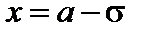 вторая производная меняет знак. Значение функции в обеих этих точках одно и то же:
вторая производная меняет знак. Значение функции в обеих этих точках одно и то же: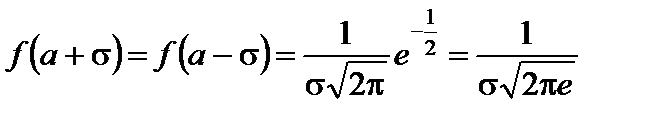 .
.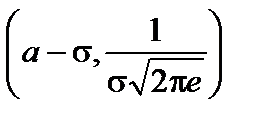 и
и 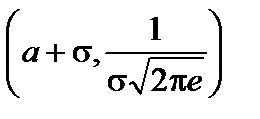 .
.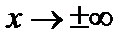 равен нулю:
равен нулю: 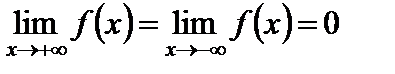 .
.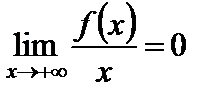 , и наклонных асимптот нет).
, и наклонных асимптот нет).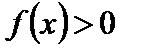 , т.е. кривая расположена выше оси Ox, а также тот факт, что кривая симметрична относительно прямой
, т.е. кривая расположена выше оси Ox, а также тот факт, что кривая симметрична относительно прямой 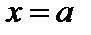 (так как разность
(так как разность 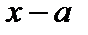 содержится в аналитическом выражении функции в квадрате).
содержится в аналитическом выражении функции в квадрате).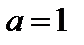 ,
, 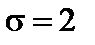 .
.



