

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Оснащения врачебно-сестринской бригады.
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Специальные методы применяются в тех случаях, когда удается использовать специфические свойства соответствующих случайных величин и их преобразований. Общих рекомендаций по специальным методам не существует. В каждом конкретном случае следует полагаться на свою квалификацию и научную интуицию.
Рассмотрим два способа моделирования случайной величины X, имеющей нормальный закон распределения с нулевым средним и дисперсией, равной единице. Напомним, что функция плотности распределения вероятностей такой случайной величины описывается выражением 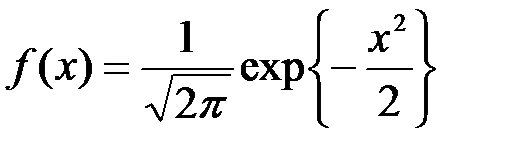 .
.
Первый метод основан на центральной предельной теореме:
если Y 1 .Y 2,, Yn — неизвестные случайные величины, имеющие одинаковый закон распределения с матожиданием m и дисперсией σ 2, то при неограниченном увеличении n закон распределения суммы
 (2.4)
(2.4)
приближается к нормальному, с дисперсией nσ 2 и матожиданием nm.
Используя датчик независимых случайных чисел Y, с законом распределения вероятностей, определяемым выражением (2.1), следует получить n таких чисел и сложить их. Учитывая, что равномерно распределенная случайная величина Y имеет моменты m = 0,5 и σ 2 =1/12, определим, что случайная величина Z в выражении (2.4) будет иметь матожидание 0,5 n и дисперсию n /12. Искомая нормированная случайная величина X получается из выражения
 . (2.5)
. (2.5)
Требуемое значение n определяется исходя из необходимой точности аппроксимации и быстродействия датчика. Известно, например, что вероятность отклонения гауссовой случайной величины от математического ожидания более чем на 3 не превышает 0,003. На практике обычно ограничиваются n = 6…12. Например, выбрав n =12 формула (2.5) примет весьма простойвид X = Z -6, что, безусловно, повысит быстродействие генератора. Рассмотренный метод прост в реализации и позволяет получить закон распределения случайной величины, очень близкий к нормальному.
|
|
Второй метод основан на свойствах следующих преобразований.
В разделе 1.6.1 было установлено, что если ξ1 и ξ2 - две независимые гауссовы случайные величины с нулевыми средними значениями и дисперсией, равной σ2, то имеет место взаимно однозначное преобразование:
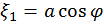
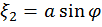 ,
,
Где 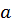 - случайная длина вектора с координатами ξ1 и ξ2, имеющая закон распределения Релея;
- случайная длина вектора с координатами ξ1 и ξ2, имеющая закон распределения Релея; 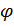 - случайное значение угла между указанным вектором и осью абсцисс, с равномерной плотностью распределения вероятностей на интервале [0, 2π], причем, случайные величины
- случайное значение угла между указанным вектором и осью абсцисс, с равномерной плотностью распределения вероятностей на интервале [0, 2π], причем, случайные величины 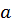 и
и 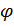 независимы так же как
независимы так же как 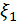 и
и 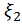 . Отсюда следует, что независимые случайные величины ξ1 и ξ2 можно получить в результате преобразования случайных величин
. Отсюда следует, что независимые случайные величины ξ1 и ξ2 можно получить в результате преобразования случайных величин  и
и 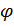 , которые необходимо предварительно сгенерировать или получить в результате преобразования базовой последовательности с равномерной плотностью распределения на интервале [0, 1].
, которые необходимо предварительно сгенерировать или получить в результате преобразования базовой последовательности с равномерной плотностью распределения на интервале [0, 1].
Моделирование случайной величины, распределенной по закону Релея, производится методом нелинейного преобразования и рассмотрено в примере 1. Моделирование случайной величины, равномерно распределенной в диапазоне [0, 2π], осуществляется изменением масштаба. Отсюда пара независимых гауссовых случайных величин и с параметрами (m = 0 и σ2 = 1) получается путем следующего преобразования двух независимых равномерно распределенных на интервале [0, 1] случайных величин у 1, у 2:
 ,
,
 ,
,
где и значения базовой последовательности с равномерной плотностью распределения на интервале [0, 1]
Этот метод позволяет получить точное нормальное распределение случайной величины, однако требует значительного времени из-за вычисления нелинейных функций. Обычно его используют, когда необходимо учитывать реализации гауссовых случайных величин с очень большим отклонением от математического ожидания, т.е. когда важны "хвосты" нормального закона распределения вероятностей.
|
|
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!